轮勺式大蒜单粒取种装置设计与试验
2020-04-01李玉华张智龙李天华吴彦强牛子孺侯加林
李玉华 张智龙 李天华 吴彦强 牛子孺 侯加林
(1.山东农业大学机械与电子工程学院,泰安 271018;2.山东省农业装备智能化工程实验室,泰安 271018)
0 引言
大蒜单粒取种[1]是实现大蒜机械化播种的关键技术之一。大蒜颗粒大、形状不规则及表面粗糙,极易产生颗粒堆积[2-3]、结拱堵塞等现象[4],从而导致漏充率高。因此,相对比较成熟的玉米取种器[5-6]、小麦取种器[7]和大豆取种器[8]等,无法通过简单改进而直接应用于大蒜单粒取种。
现有大蒜单粒取种方式主要有勺链式、勺带式、夹持式及振动式等[9-10]。大蒜属于中大籽粒种子,其形状尺寸变异系数大,大蒜取种器漏充及重充现象难以避免,勺链及勺带式取种器结构简单,但中高速时振动明显,易引起掉种。近年来有学者对大蒜取种进行了研究,耿爱军等[11]采用链勺式结构进行大蒜单粒取种,对取种勺及链板进行了优化;此外有学者对大籽粒种子取种器[12-15]进行了研究,为大蒜单粒取种装置设计提供了技术参考。
针对大蒜单粒取种的漏播及重播问题,阐述轮勺式大蒜单粒取种装置的工作原理,利用数理统计[16-17]方法对取种勺的结构尺寸区间进行分析。通过离散元仿真软件EDEM[18-20]对取种过程及取种勺结构参数进行仿真分析,利用Box-Benhnken中心组合设计理论设计试验方案[21-23],并进行台架验证试验,以期为大蒜单粒取种装置的设计提供参考。
1 取种器结构与工作原理
1.1 取种器结构
轮勺式大蒜取种器主要由种箱、驱动电机、取种轮、取种勺组成,结构如图1所示。
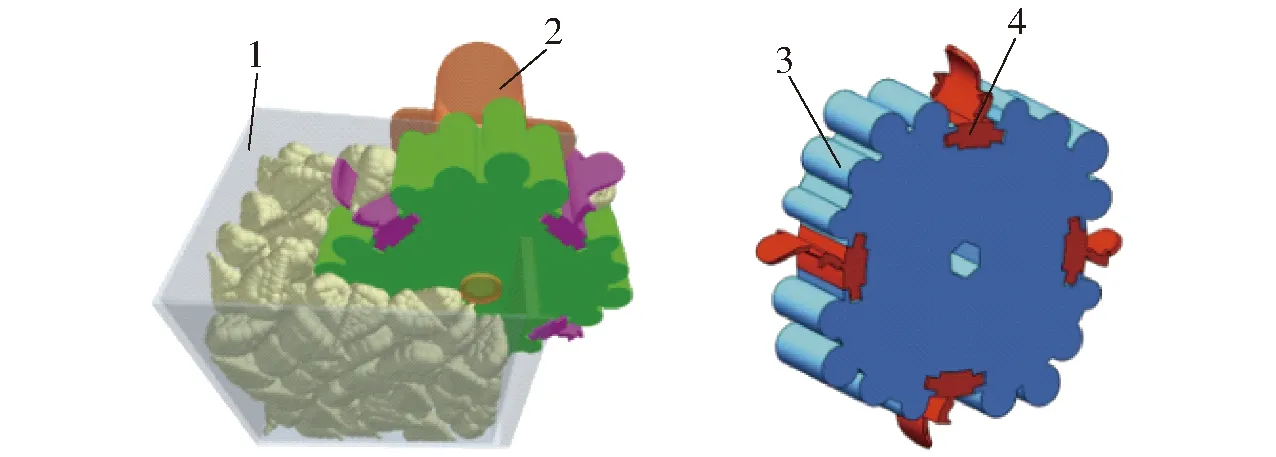
图1 轮勺式大蒜取种器结构示意图
取种勺与取种轮通过圆弧面配合,可方便拆卸及更换。驱动电机通过传动轴驱动取种轮运动,取种轮带动取种勺旋转,取种勺与大蒜通过搅动挤压使其进入取种勺空腔实现取种。
1.2 单粒取种原理
大蒜单粒取种过程分为4个阶段,如图2所示,分别为:取种区、输种区、排种区和过渡区。
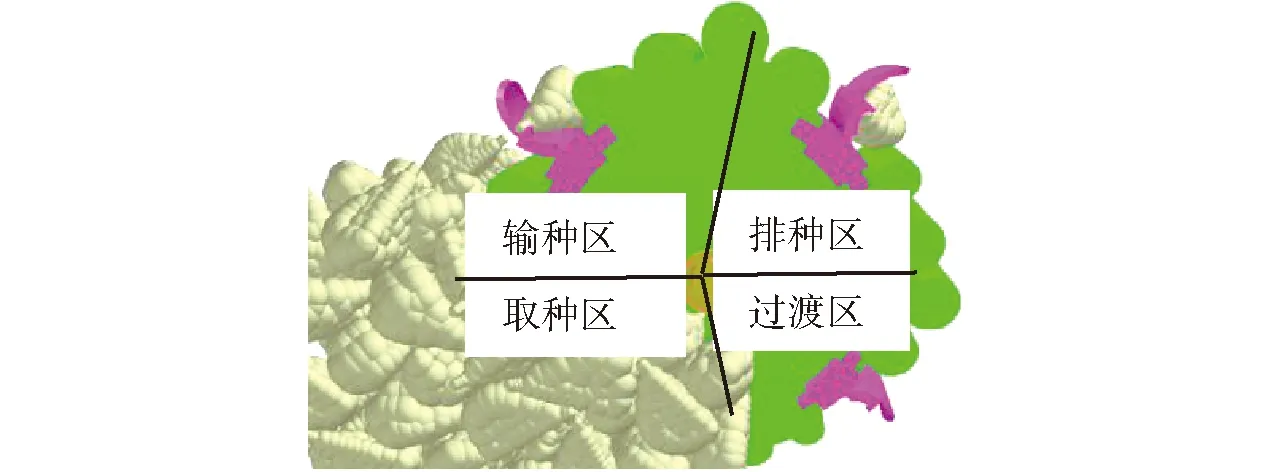
图2 轮勺式大蒜取种器工作示意图
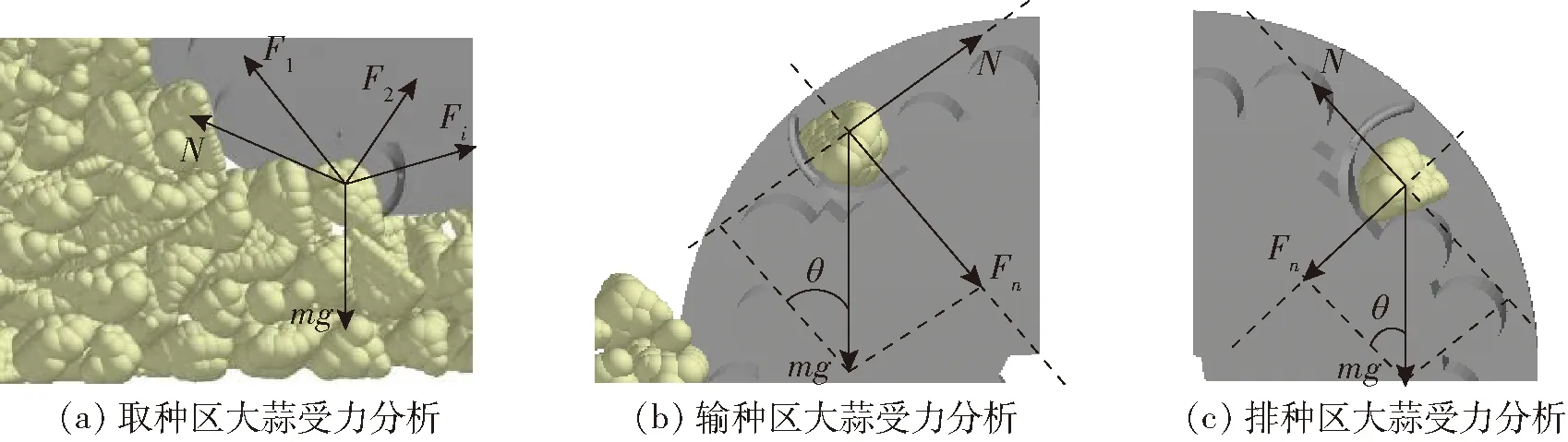
图3 取种过程大蒜受力分析
取种过程分析:取种区中进入取种勺的待取大蒜受到自身重力、周边大蒜及取种勺的作用力,如图3a,受力公式为
(1)
式中m——大蒜质量,kg
Fi(i=1,2,…,n)——周围大蒜对待取大蒜的作用力,N
N——取种勺对大蒜的支持力,N
a——待取大蒜的加速度,m/s2

Mo——大蒜所受力对支撑点的力矩,N·m
按取种勺内有大蒜和无大蒜两种情况对大蒜运动状态进行分析:取种勺内无大蒜时,待取大蒜将在取种勺周围大蒜的挤压及勺壁的支撑力作用下进入取种勺的空腔内;取种勺内已有大蒜时,勺内大蒜受到周围大蒜及取种勺的作用力,此时取种勺周围大蒜处于竞争状态,勺内大蒜将趋于更加稳定,否则将被周边大蒜替代,因此经过取种区后勺内大蒜处于稳定状态,不易在输种区滑落而引起漏种。
输种过程分析:输种区中取种勺的大蒜将在自身重力和取种勺的支撑力作用下做匀速圆周运动,如图3b,受到重力及取种勺的支撑力,径向方向受力公式为
(2)
式中ω——取种轮角速度,rad/s
r——取种轮半径,m
θ——取种勺、取种轮中心连线与水平方向夹角,rad
Fn——大蒜匀速圆周运动所需向心力,N
当重力产生的分力小于向心力时取种勺中的大蒜将沿切向方向滑出而产生漏种,取种勺提供的向心力与ω、r、θ及取种勺轮廓密切相关,需满足ω2r≤gsinθ。
排种过程分析:排种区的大蒜将在自身重力和取种勺的支撑力作用下做匀速圆周运动,如图3c,随θ的减小重力分量无法提供足够的向心力,使大蒜沿切向方向飞出完成排种。
2 关键结构设计与仿真
大蒜具有籽粒大、形状极不规则和个体差异大等特点,因此易产生漏播和重播现象,本文以概率统计的大蒜外形尺寸为依据对大蒜单粒取种器进行了设计,分析了取种勺的形状、尺寸及取种轮转速对单粒取种性能的影响。
2.1 大蒜三维尺寸
大蒜外形为非规则的类扇形体,其长度Ld、宽度Wd、厚度Td对取种勺尺寸影响最大,本文以金乡大蒜为研究对象,随机选取100粒饱满的大蒜进行测量,结果如表1所示。

表1 大蒜三维尺寸
对所测数据的概率分布进行分析,概率密度曲线如图4所示,各尺寸基本符合正态分布,其中Ld~N(32.38,2.222),Wd~N(16.32,3.162),Td~N(18.98,2.912),取种勺尺寸参数设计以此大蒜三维尺寸分布为依据。

图4 大蒜三维尺寸概率分布
2.2 离散元仿真模型
为缩短试验时间,提高试验针对性,本文采用离散元分析软件EDEM对取种器取种性能进行仿真分析。以饱满的金乡大蒜为仿真分析对象,大蒜颗粒的尺寸根据体积按正态分布进行设置。颗粒间及颗粒与设备间的接触模型均采用Hertz-Mindlin(no slip)模型,仿真参数如表2所示[24]。
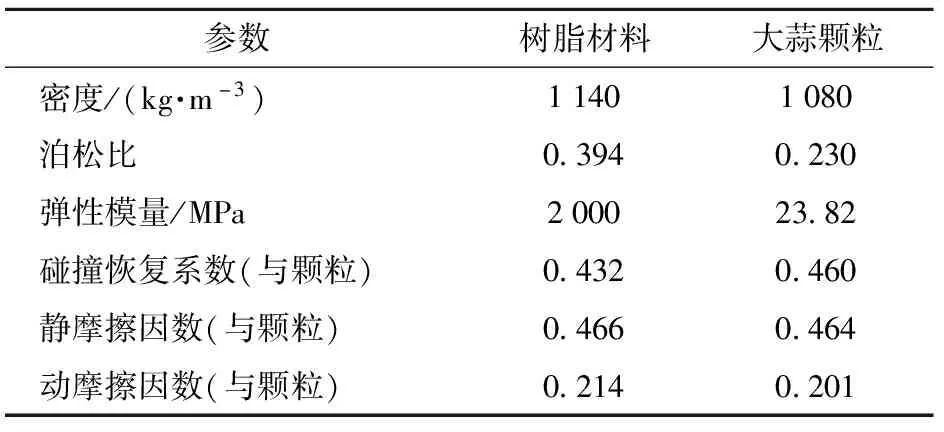
表2 仿真参数
2.3 取种勺设计与仿真分析
取种勺是大蒜单粒取种器的核心部件,其结构和尺寸均对漏充率和重充率具有直接的影响。
2.3.1取种勺结构的确定
通过离散元分析软件对多种不同结构的取种勺进行仿真分析,对比分析发现图5所示的4种取种勺结构的取种性能相对较好,其中D型取种勺漏充率和重充率在相同条件下比其他3种结构低,本文选用D型取种勺进行结构参数优化。
A型取种勺漏充率及重充率均相对较高,因该取种勺弧高恒定,取种勺容积大,容易一次取两粒大蒜,且取种勺两端开口在输种阶段大蒜会从两端掉落导致较高的漏充率;B型取种勺弧高恒定且两端封闭,虽然漏充率较低但重充率较高;C型取种勺的中间大两端小,重充率低,但两端开口导致漏充率较高;D型取种勺弧高中间大两端小,且两端的边缘凸起能避免大蒜在输种过程中滑落,克服了B、C两种结构的缺点而保留了其优点,因此D型取种勺具有相对较低的重充率和漏充率。
2.3.2取种勺尺寸的确定
取种勺的关键结构参数为半径R、长度L和弧高H。为保证单粒取种成功率,取种勺尺寸需要在合适的范围内。
为保证在取种勺长度方向不能同时容纳1粒以上蒜种且空间尽量大以提高取种率,取种勺长度L需满足
(3)
由多个相互独立随机变量函数分布的性质知:2Ld~N(64.76,4.442),Ld+Wd~N(48.7,3.862),Ld+Td~N(51.36,3.662)。式(3)各约束条件对应的分布函数曲线如图6所示,随L取值增大重充率升高而漏充率降低,为保证单粒取种合格率,计算分析得L取值范围为35.00~45.00 mm时能两者兼顾,当L为45.00 mm时重充率为14.50%。

图6 取种勺长度L取值区间
为保证在取种勺深度方向取种后不滑落且不能同时容纳1粒以上蒜种,取种勺的弧高H需满足
(4)
由多个相互独立随机变量函数分布的性质知:1.5Wd~N(24.48,4.742),1.5Td~N(28.47,4.372),0.5Wd~N(8.16,1.582),0.5Td~N(9.49,1.452)。式(4)各约束条件对应的分布函数曲线如图7所示,随H取值增大重充率升高而漏充率降低,为保证单粒取种合格率,计算分析得H取值范围为13.00~17.00 mm。仿真和单因素试验发现弧高H在此区间范围内对单粒取种性能影响不大。
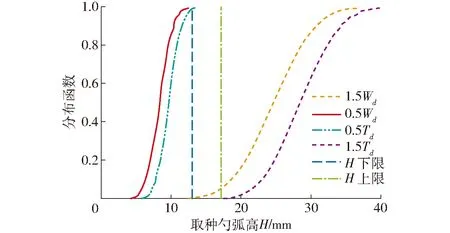
图7 取种勺弧高H取值区间
为保证在取种勺宽度方向单粒取种成功率,取种勺的弦长S需满足
(5)
由多个相互独立随机变量函数分布的性质知:2Wd~N(32.64,6.322),2Td~N(37.96,5.822),Wd~N(16.32,3.162),Td~N(18.98,2.912)。式(5)各约束条件对应的分布函数曲线如图8所示,随S取值增大重充率升高而漏充率降低,为保证单粒取种合格率,同时考虑弧高的限制,并通过先期试验验证,S取值范围为26.5~34.0 mm时取种效果较好。

图8 取种勺弦长S取值区间
由三角几何关系知取种勺半径R满足
(6)
把弧高H及弦长S的取值范围代入式(6),计算得取种勺半径R取值范围为13.30~17.00 mm。
2.3.3取种轮设计与仿真分析
取种轮外圆弧面与取种勺配合形成取种空腔,取种轮外形对取种合格率有显著影响。通过仿真及试验发现:取种轮外圆面采用由多个凸起圆柱面组成的异型面结构时(图9a),重种现象较少,落种位置一致,因为在圆柱面的法向力作用下大蒜无法在取种轮的表面堆积,且凸起的圆柱面对将进入取种勺的大蒜进行搅动避免产生堆积和结拱堵塞现象的发生;取种轮为规则圆面时(图9b),大蒜会在取种勺与取种轮的表面产生堆积,重种现象显著,落种时刻提前且蒜种下落时易与上一个取种勺发生碰撞导致落种轨迹不一致。

图9 取种轮外形对取种效果的影响
3 试验与结果分析
3.1 试验材料与设备
试验设备为搭建的大蒜单粒取种试验台,结构如图10所示,主要包括支架、种箱、直流驱动电机、调速器、取种轮、取种勺等。驱动电机转速0~40 r/min连续可调。支架及种箱采用透明PVC板加工而成,便于取种过程观察。

图10 取种器试验装置
3.2 试验方法
试验方法参考GB/T 6973—2005《单粒(精密)播种机试验方法》进行。由于漏充率、重充率和合格率之和为100%,因此选漏充率y1和合格率y2为评价指标,漏充率和合格率数据通过试验过程录像统计得到。
为确定最优单粒取种装置工作参数,选取对取种性能影响较大的取种勺半径R、长度L和取种轮转速为试验因素,漏充率和合格率为响应指标。根据前期理论计算、仿真分析及单因素试验确定各因素取值范围:半径R为14.0~18.0 m,取种勺长度L为35~45 mm,取种轮直径为130.00 mm时,取其转速为5.0~20.0 r/min。依据Box-Benhnken中心组合设计理论进行试验设计,试验因素编码如表3所示。
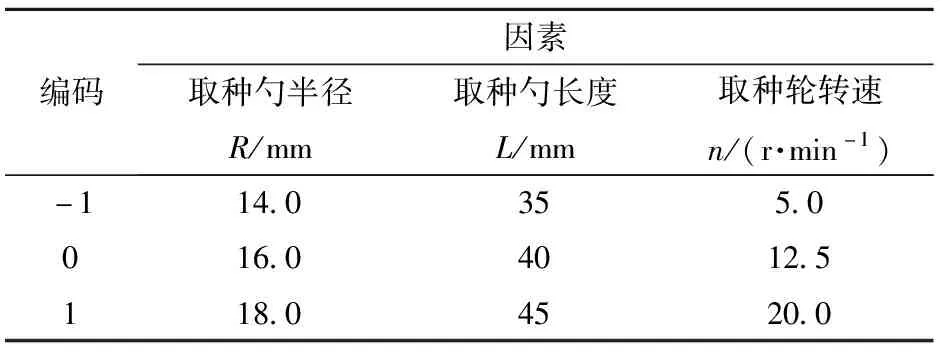
表3 试验因素编码
3.3 结果与分析
3.3.1试验结果
试验设计方案与结果如表4所示,其中x1、x2、x3表示各因素编码值。
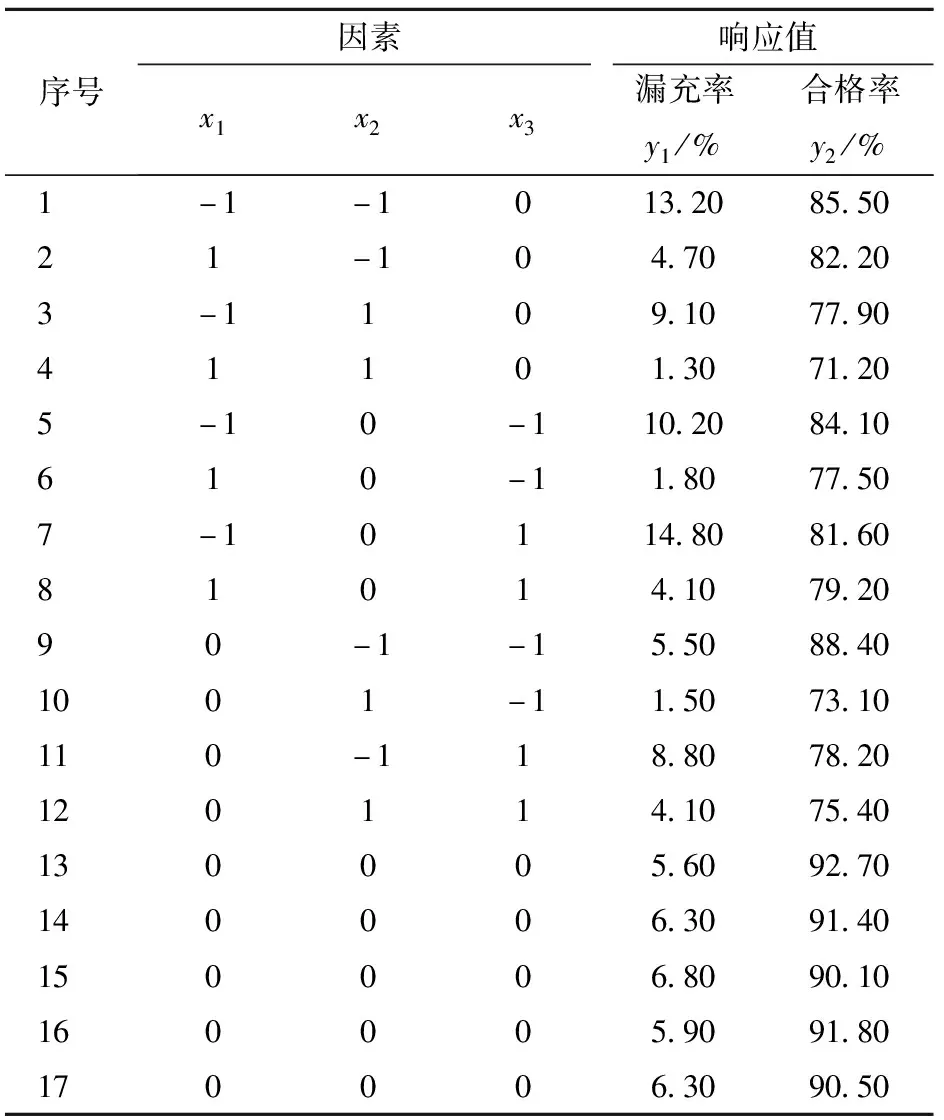
表4 试验设计方案及结果
3.3.2回归模型建立与显著性检验
对表4中的试验结果,运用Design-Expert 11.1.2.0数据分析软件进行多元回归拟合分析,得到漏充率y1和合格率y2的回归方程
y1=6.18-4.42x1-2.02x2+1.6x3+
0.18x1x2-0.58x1x3-0.18x2x3+

(7)
y2=91.3-2.38x1-4.59x2-1.09x3-
0.85x1x2+1.05x1x3+3.13x2x3-

(8)


表5 回归模型方差分析
注:*表示影响差异显著(P<0.05);** 表示影响差异极显著(P<0.01)。
3.3.3影响因素分析
(1)各因素对漏充率的影响
固定某个因素水平为零,分析另外2个因素的相互作用对漏充率的影响,其响应曲面如图11所示。
图11a为取种轮转速处于中心水平时,取种勺半径及其长度交互作用对漏充率的影响。随取种勺半径及长度的增加,漏充率逐渐减小。图11b为取种勺长度处于中心水平时,取种勺半径及取种轮转速交互作用对漏充率的影响。取种勺半径一定时,随取种轮转速升高,漏充率逐渐增大。当取种勺半径增大时,会减弱因取种轮转速升高引起的漏充率升高的趋势。图11c为取种勺半径处于中心水平时,取种勺长度及取种轮转速交互作用对漏充率的影响。取种勺长度一定时,随取种轮转速升高,漏充率逐渐增大。当取种轮转速一定时,随取种勺长度增加漏充率降低。

图11 各因素对漏充率的影响

图12 各因素对合格率的影响
(2)各因素对合格率的影响
固定一个因素水平为零,分析另外2个因素的相互作用对合格率的影响,其响应曲面如图12所示。
图12a为取种轮转速处于中心水平时,取种勺半径及其长度交互作用对合格率的影响。取种勺长度一定时,随着取种勺半径增大,合格率先升后降。取种勺半径一定时,随着取种勺长度增大,合格率先升后降。图12b为取种勺长度处于中心水平时,取种勺半径及取种轮转速交互作用对合格率的影响。取种勺半径一定时,随着取种轮转速增大,合格率先升后降。取种轮转速一定时,随着取种勺半径增大,合格率先升后降。图12c为取种勺半径处于中心水平时,取种勺长度及取种轮转速交互作用对合格率的影响。取种勺长度一定时,随着取种轮转速增大,合格率先升后降。取种轮转速一定时,随着取种勺长度增大,合格率先升后降。
3.3.4参数优化与试验验证
以漏充率y1最低、合格率y2最高为目标函数,以取种勺的半径x1、长度x2和取种轮转速x3为约束条件,建立大蒜单粒取种装置工作参数规划数学模型
(9)
利用软件Design-Expert 11.1.2.0 Optimization Numerical模块进行优化,得最佳参数组合为:取种勺的半径16.32 mm、长度38.46 mm,取种轮转速9.9 r/min。此时模型预测的漏充率为5.49%,合格率为91.59%。
为验证优化结果的准确性,设定工作参数为:取种勺半径16.30 mm、长度38.50 mm,取种轮转速10.0 r/min。在大蒜单粒取种试验台进行3次重复试验,取平均值为试验值,试验结果为漏充率5.50%,合格率91.10%。结果对比表明理论优化值和试验验证值非常接近,回归模型可靠。
3.4 讨论
本文的研究对象是未经过筛选分级的大蒜,采用基于数理统计的理论进行取种勺的结构参数设计。由于大蒜外形尺寸变异系数较大,为满足所有大蒜的成功取种率采用了折中的方案,因此漏充率及重播率略高,如果大蒜播种前进行筛选分级,并针对不同等级的大蒜采用不同结构参数的取种勺,取种合格率将会显著提高。
4 结论
(1)设计了一种轮勺式大蒜单粒取种装置,利用取种勺与取种轮形成的空腔进行单粒取种,取种勺与周边大蒜相互挤压作用力下大蒜处于相互竞争状态,并最终使某粒大蒜在空腔内稳定,实现单粒取种。
(2)对取种区、输种区和排种区的大蒜进行了受力分析,阐述轮勺式大蒜单粒取种的原理。通过离散元仿真分析对不同取种勺及取种轮的结构形状进行了对比优化,确定了取种勺及取种轮最优结构。采用数理统计的方法确定了取种勺的尺寸区间,为取种勺设计提供了数据支持。
(3)采用Box-Benhnken中心组合方法进行了三因素三水平回归正交试验,分别建立漏充率和合格率多元回归模型,以漏充率和合格率为目标,对各影响因素参数进行了优化。最优参数组合为:取种勺半径16.30 mm、取种勺长度38.50 mm、取种轮转速10.0 r/min。在最优参数组合下进行了台架试验,此时漏充率为5.50%,合格率为91.10%,与模型预测结果吻合。
