基于SVM的煤与瓦斯突出预测模型及应用

2020-03-31王建

陕西煤炭 2020年2期

王建

(晋城煤业集团寺河煤矿二号井，山西晋城 048000)

0 引言

煤与瓦斯突出是制约矿井开采的重大问题之一[1]。探讨矿井内煤与瓦斯突出的问题，从而及时地遏制事故的发生，对于矿井的安全生产具有很重要的意义。目前，国内外的许多专家学者对煤与瓦斯突出的预测进行了大量的研究与探讨[2-5]，并且也提出了相关的预测模型[6-12]。为解决原有预测方法精度较低，且所选择的样本受到限制的情况，在以往对煤与瓦斯突出研究的基础上，提出PSO-SVM以及GA-SVM的煤与瓦斯突出预测模型，对矿井内煤与瓦斯突出进行预测与研究。此外，将矿井实测参数当作训练和检验样本，建立两种不同算法的分类预测模型，最后对两种算法进行对比分析，以期对煤与瓦斯突出的预测提供必要的借鉴。

1 SVM参数优化算法及预测模型

1.1 SVM参数优化算法

粒子群优化算法支持向量机模型：构建粒子群优化算法支持向量机的分类预测模型算法的步骤如下。①对粒子群优化算法的基本参数进行初始化设置；②明确搜索空间的大致范围，分别对支持向量机模型中的相关参数进行确定，例如惩罚因子以及宽度函数；③明确适应度函数，本文中的适应度函数为K折交叉验证的准确率，根据交叉验证的思想能够有效地选取惩罚因子以及核函数的相关参数；④对本身的最优解进行计算，此最优解一般用Pbest来表示；⑤对全局种群中的最优解进行计算，此最优解用Gbest来表示；⑥利用Pbest以及Gbest对各个粒子的速度及其位置进行更新；⑦粒子群优化算法结束，返回到第3个步骤继续操作，搜寻到符合终止的条件而结束。

根据粒子群优化算法整体寻优得到的最优解及所构建的PSO-SVM模型流程图如图1所示。

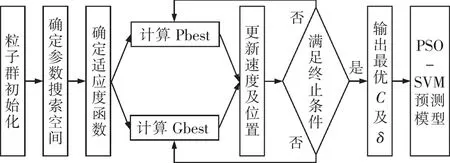
图1 PSO-SVM模型流程图

遗传优化算法支持向量机模型：通过对遗传算法相关知识的研究可知其在处理非线性问题中具有一定的搜寻能力。所以，在选择支持向量机的最佳参数中，可以看作对惩罚因子以及核函数的优化处理的过程。基于此，本文中提出根据遗传算法优化的支持向量机的分类预测模型，其模型算法如下。①二进制编码，第一步要给初始支持向量机中的惩罚因子C以及核函数参数δ一个范围比较大的搜寻空间，第二步即可在此空间内把惩罚因子C以及核函数参数δ的数值替换成可以被遗传算法接受的染色体；②明确适应度函数，本文中的目标函数为3折交叉验证的准确率，根据交叉验证的思想能够有效地选取惩罚因子以及核函数的相关参数；③使初始的种群产生出来，对各个个体的适应度进行计算分析，明确适应度的标准准则；④依次进行一系列的操作—选择、交叉及变异，对适应度的数值进行更新；⑤判定其是否达到计算停止的条件，如果适应度的值和设定的标准值几乎没有差别时，则可以输出最佳解；相反，不符合时返回到第四步继续操作直到符合要求；⑥根据最佳C与δ建立遗传优化算法支持向量机的预测模型，其流程图如图2所示。

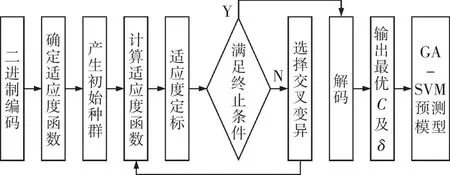
图2 GA-SVM流程图

1.2 预测模型

PSO-SVM预测模型：基于Matlab并且结合SVM工具箱，编写出矿井内煤与瓦斯突出的PSO-SVM程序，最后优化处理惩罚因子C以及核函数参数δ。①对PSO-SVM模型的初始参数进行设定：惩罚因子C的搜寻范围在0.1～100；参数δ的搜寻范围在0.1～1 000；粒子规模是20，循环迭代次数是200；②利用3折交叉验证的思想，把其准确率看作适应度函数，进行计算并读取样本基础参数；③如果程序运行到满足停止的条件时即可终止，其粒子的最佳以及平均适应度如图3所示。

图3 粒子种群适应度

由图3可以看出，3折交叉验证的准确率约为83.333%，得到的最优参数惩罚因子C=0.1，核函数参数δ=750.062 8。

GA-SVM预测模型：基于Matlab并且结合SVM工具箱，编写出矿井内煤与瓦斯突出的GA-SVM程序，最后优化处理惩罚因子C以及核函数参数δ。对初始参数进行设定：①二进制编码，其惩罚因子C的搜寻范围在0.1～100；参数δ的搜寻范围在0.1～1 000；粒子规模为20；轮盘法代沟以及重组率分别设定为0.9与0.7，循环迭代次数是200；②使程序自动运行，把样本的相关参数读入且计算到迭代终止，其粒子的最佳以及平均适应度如图4所示。

图4 遗传进化过程

根据图4可知，3折交叉验证的准确率约为91.667%，得到的最优参数惩罚因子C=12.016 1，核函数参数δ=0.110 34。

2 SVM在煤与瓦斯突出预测中的应用

2.1 影响因素分析

造成矿井内部煤与瓦斯突出的因素很多，例如矿井地质情况、瓦斯的影响以及煤体内部构造等[13-14]。本文根据不同的因素在煤与瓦斯突出中所占比重的大小以及是否便于检测，选用以下几个指标当作样本属性，分别为：瓦斯放散初速度X1(mL·s-1)及其压力X2(MPa)、煤体内部破坏类型X3、煤的坚固性系数X4、开采深度X5(m)。其中，煤体内部的破坏类型分别有以下几种情况：无破坏煤体；有一定的破坏煤体；煤体破坏严重；煤体粉碎；全粉煤。

2.2 危险等级的选择

通过收集整理，可以得到最初的训练样本，其中取前11个样本作为训练样本，后3个样本看作是验证样本。根据煤与瓦斯突出时的煤体的重量将其分为4个类别：没有突出危险时标记为无(1)，小于50 t的突出标记为小(2)，50～100 t标记为中(3)，大于100 t记为大(4)，其原始数据见表1。

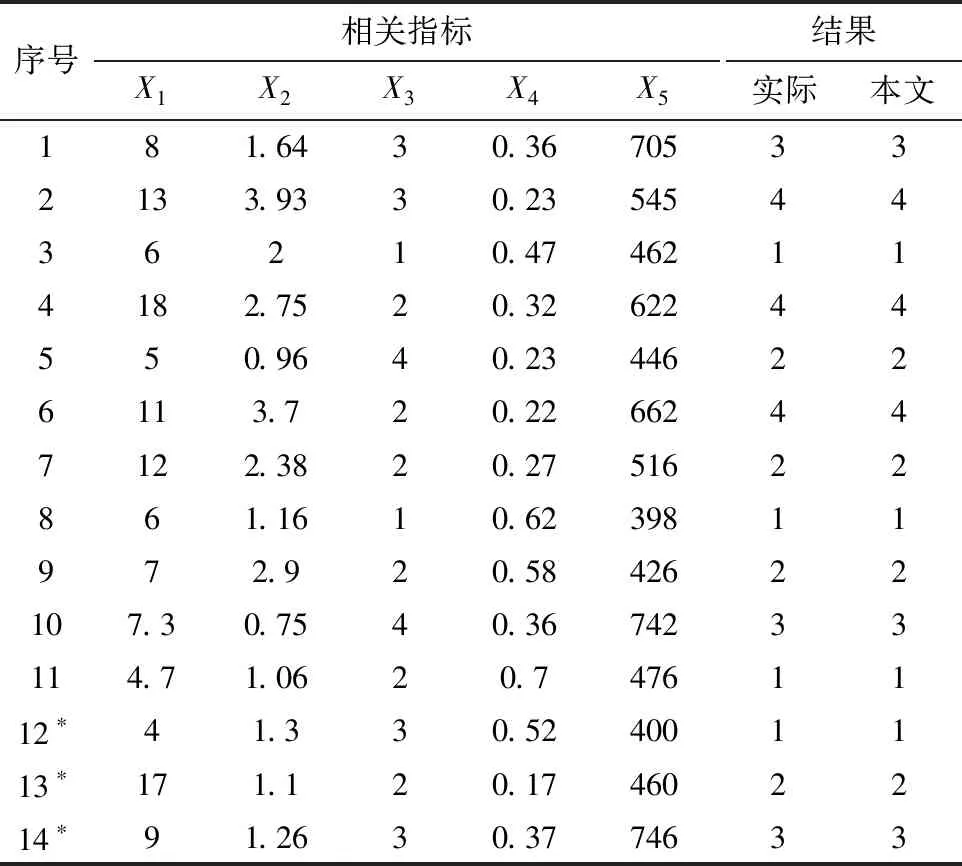
表1 训练与验证样本原始数据

2.3 预测结果分析

PSO-SVM模型：根据最优参数构建出PSO-SVM模型，从而对后3组的测试样本进行预测分析，其预测结果如图5所示，从图中可以看出实际和预测结果基本相同。

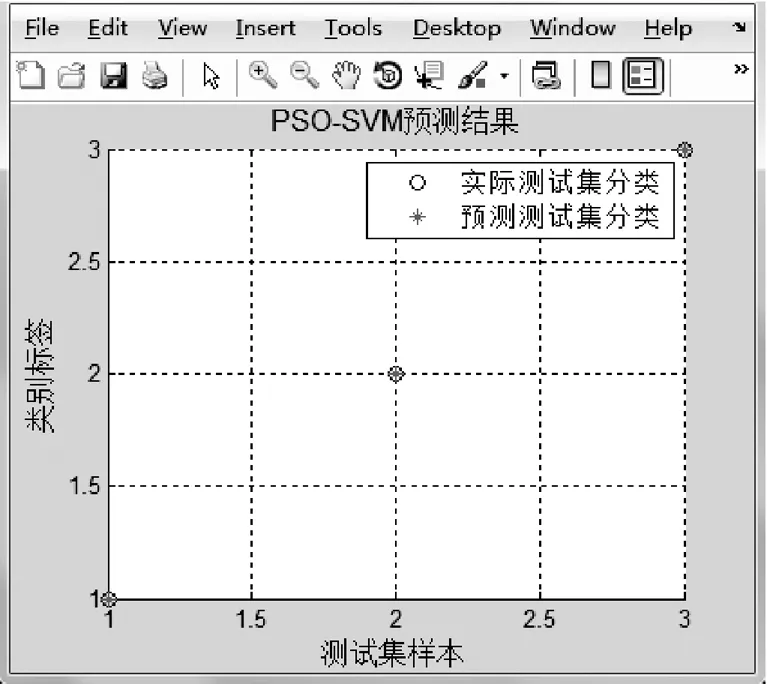
图5 PSO-SVM仿真结果

GA-SVM模型：根据最优参数构建出GA-SVM模型，并且对后3组测试样本进行预测分析，其仿真预测结果如图6所示，由图可知仿真结果有1处误判，把煤与瓦斯突出危险程度小误判为大。

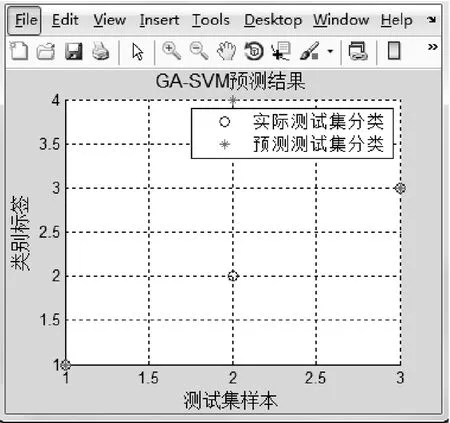
图6 GA-SVM仿真结果

根据构建的PSO-SVM以及GA-SVM的突出分类预测模型，并且结合实际矿井进行实验，可知这两种算法在矿井的瓦斯突出预测中效果明显。而由最终的仿真结果得出的粒子群优化算法相对于遗传算法而言，综合预测结果更加准确，显示出其强大的通用性能，运行方便简单，具有一定的推广价值。

3 工程应用

根据实际地质勘查，寺河煤矿二号井煤层具有煤与瓦斯突出的危险性。以寺河煤矿二号井中的8个突出严重的区域为研究对象，将几个突出的相关参数当作预测的样本进行预测分析，并且根据构建的PSO-SVM和GA-SVM模型对该矿二号井中瓦斯突出区域进行预测，其结果如图7、8所示。根据表2，可以看出在BP网络预测下的单项以及综合指标的预测结果。

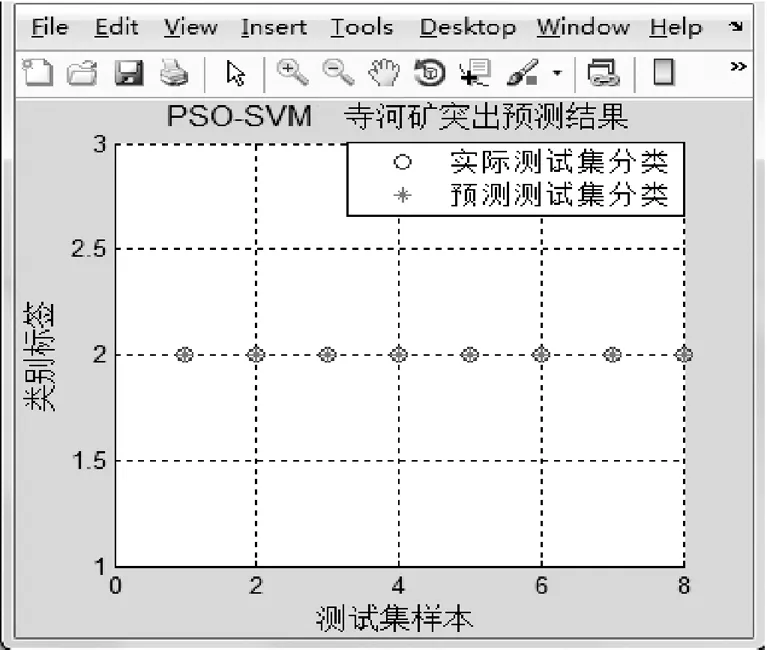
图7 PSO-SVM仿真预测结果

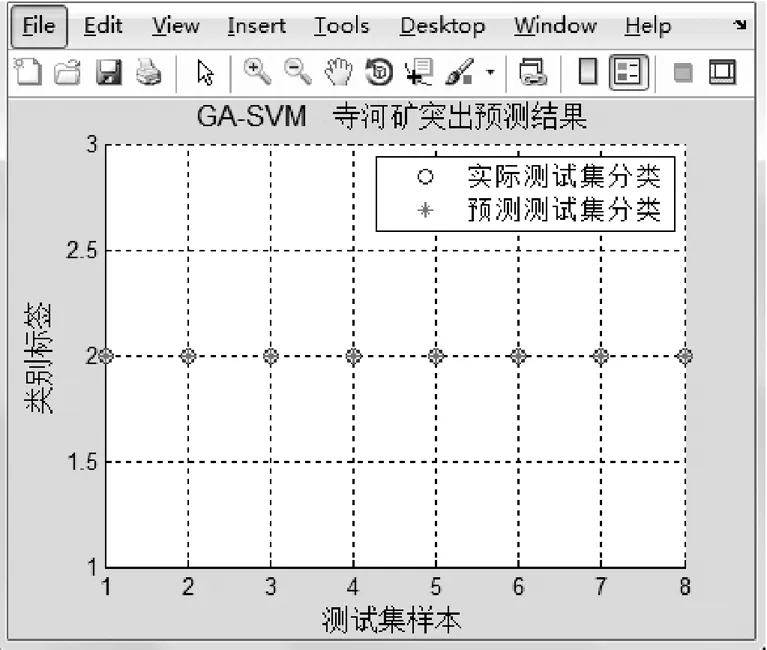
图8 GA-SVM仿真预测结果

表2 模型预测结果

由表2可以看出，单项以及综合指标的预测结果和实际矿井的突出情况有些差异，其准确度较低，并且体现不出矿井瓦斯突出危险程度的大小。利用20个具有代表性的样本对BP神经网络进行训练，可知预测的突出情况和实际情况相符合，然而把样本的个数降到11个时，其预测结果有5处误差。因此，可以说明在预测矿井内煤与瓦斯突出时，BP神经网络在处理小样本数据时并不准确。而同样在小样本的情况下，采用PSO-SVM模型对寺河煤矿二号井的突出类型进行预测，其结果与实际相符合，进一步验证了PSO-SVM模型在处理小样本的过程中有很强的泛化能力，可以及时解决矿井内煤与瓦斯突出中样本较少的情况。