重力资料处理中的坐标转换问题研究
2020-03-31郑庆敏
郑庆敏
(海南省海洋地质调查研究院,海南 海口 570100)
在地球外部重力场的相关研究领域,如大地水准面的精化、外部重力场的逼近等都需要处理大量的重力观测资料以得到具有重要使用价值的重力场元素[1-3]。地球外部重力场的大量计算均需要重力点精确地心坐标,即地心经纬度和地心距,由于各种重力资料的来源、时期等的差异,致使已有重力测点的坐标信息良莠不齐。根据相关知识,只有测点具备了的全部精确大地坐标,即大地经纬度和大地高的情况下才能转换得到其精确地心坐标[3-5],而目前我国大部分物理大地测量试验区的大量重力点的坐标是大地经纬度和水准高程,并不具备完整的三维空间坐标,显然,重力资料的现实情况和实际要求是矛盾的。
上述问题产生的原因是我国的重力网建设和三维坐标控制网的建设不同步造成的。我国重力网的建设,从1957国家重力基本网(简称“57网”)到1985国家重力基本网(简称“85网”),再到最新的“2000国家重力基本网”(简称“2000网”),基准点、基本点和引点的数量、点位分布合理度、覆盖面和精度都有了很大的进步[6-7]。相较之下,我国的三维坐标基准的建设则是始于上世纪90年代初,如国家GPS A级网于1992年布测,GPS B级网于1991~1995年布测,全国GPS一、二级网则是于1991~1997年布测,中国地壳运动观测网络则是从1998年开始布测。直到2008年7月1日我国正式启用2000国家大地坐标系,才标志着实际测量工作进入了具备三维空间坐标的时期。然而,在此之前所完成的多数重力测量工作因为种种原因而与三维空间坐标的关系没有那么密切。在我国的重力控制网中,除了高等级的基准点、基本点、引点及其他重要重力控制点具备完整的三维空间坐标信息,甚至具备高等级的天文坐标信息,其他大多数的低等级重力点的高程坐标多是通过导线测量、水准测量、三角高程导线等确定的,只有少数的重力点具备较可靠的GPS测量成果。再考虑到目前相对重力测量中使用的精度最高的CG-5相对重力仪,其测点的GPS坐标也只是依靠一个粗定位的单天线而获得的结果[8-9],坐标精度可想而知。
显然,对我国重力网中坐标信息不完备的大量低等级重力点进行三维空间坐标的补测是不现实的,因此需要寻找其它途径来改善这一问题。本文针对具有大地经纬度和水准高信息的重力点,研究采用何种方法才能获得比较精确的地心坐标,其核心则是地心纬度的计算[10]。目的是在重力点位坐标的确定过程中,将坐标转换导致的误差控制在较低的程度,从而可靠地用于地球外部重力场的各种计算过程中。
1 具备大地高条件下的严密转换过程
如图1所示,在大地坐标系O-XYZ中,已知P点大地坐标(L,B,H),要获得其精密地心坐标(相对于大地坐标系参考椭球的质心),一般需要按照如下两个步骤来实现[6,10]
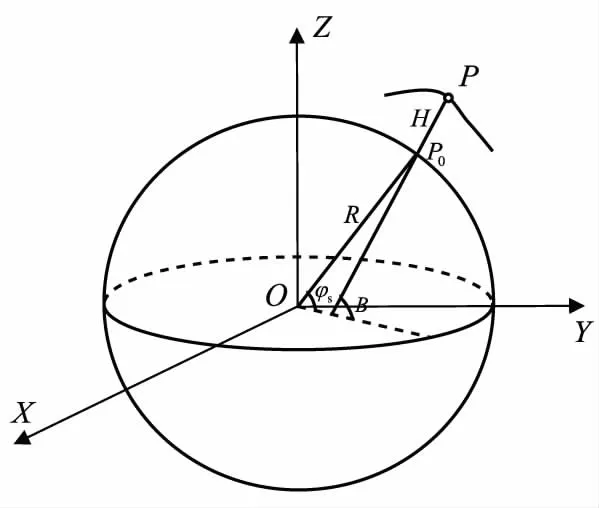
图1 大地坐标与地心坐标
1.1 根据大地坐标(L,B,H)计算地心直角坐标(X,Y,Z)如式(1)所示:
X=(N+H)cosBcosL
Y=(N+H)cosBsinL
Z=(N(1-e2)+H)sinB
(1)
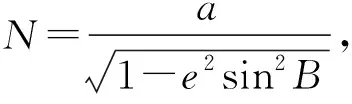
1.2 由地心直角坐标(X,Y,Z)计算地心球坐标(λ,φ,r)如式(2)所示。
(2)
式(2)中的地心经纬度的公式还可以表示为:
λ=L
(3)
(4)
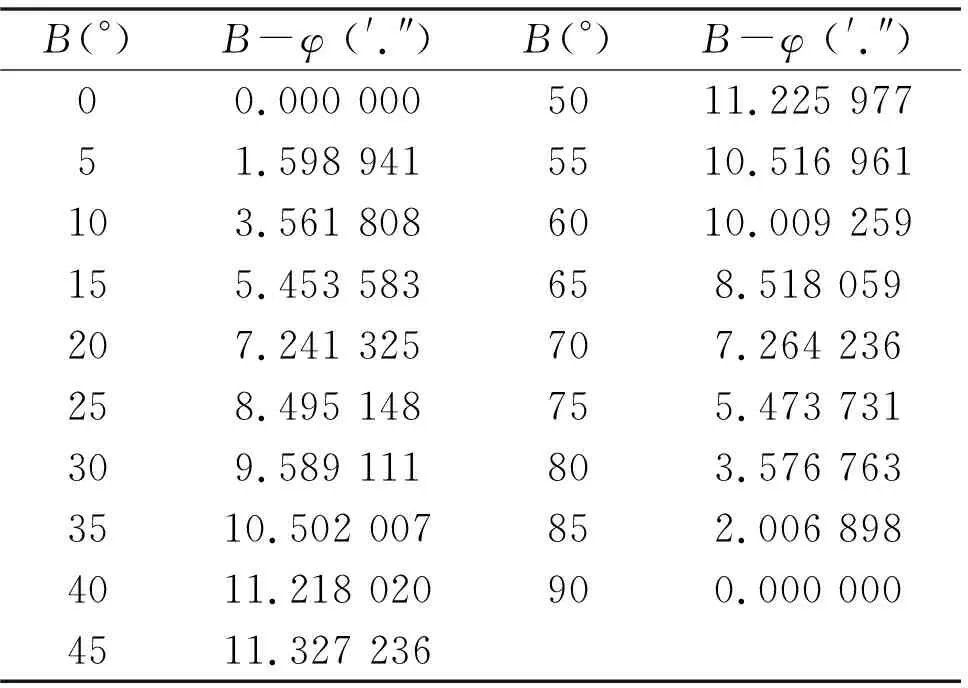
显然,经度在转换前后是不变的,而地心纬度φ则是大地纬度和大地高的函数,φ和B之间存在着明显的差异,这里给出B-φ在B∈[0,90]区间的变化趋势(取大地高为0),如图2和表1所示,此差值在大地纬度为45°时达到最大值11′32″.723 6,而在赤道和两极时均为0。这也意味着在我国范围内进行的重力场计算中,是不能使用大地纬度来代替地心纬度的。
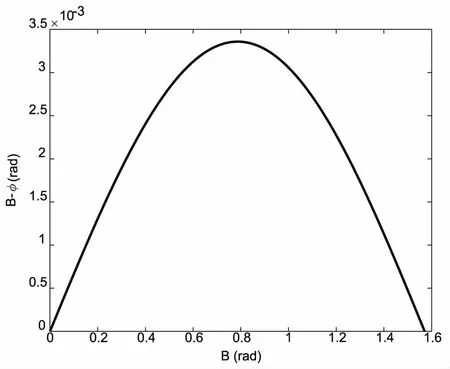
图2 B-φ在B[0, 90]区间的变化趋势(H=0)
表1B-φ在B[0, 90]区间的变化趋势(H=0)
B(°)B-φ ('.″)B(°)B-φ ('.″)00.000 0005011.225 97751.598 9415510.516 961103.561 8086010.009 259155.453 583658.518 059207.241 325707.264 236258.495 148755.473 731309.589 111803.576 7633510.502 007852.006 8984011.218 020900.000 0004511.327 236
图3表示的是在B=45°处,B-φ在H[0, 3 000]m区间的变化趋势,随着大地高的增加,大地纬度与地心纬度之差呈现出线性衰减的特点,对应的地心纬度从44°48′27″.2 764(H=0)增加至44°48′27″.6 026(H=3 000)。

图3 B-φ在H[0, 3 000]m区间的变化趋势(B=45°)
在涉及重力资料处理的背景下,大地纬度是已知量,而大地高则是含有一定的误差的,进一步得到地心纬度对大地高的偏导数如下式:
(5)
从式(5)可知:地心纬度、大地高、大地纬度之间的关系比较复杂,因此对缺乏精确大地高信息的重力资料而言,若要获得重力资料的精密地心纬度是比较困难的。另外,由于无法获得精确的地心坐标,亦无法直接利用下式计算大地水准面高Ng,
(6)
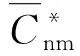
2 不具备大地高情况下的近似转换过程
大地高的定义如图所示,H=Ng+h。式中,Ng为大地水准面高,h为水准高程。亦可根据似大地水准面来定义大地高,H=Hγ+ξ,式中,Hγ为正常高,ξ为高程异常。
为解决不具备大地高情况下获取地心纬度的突出问题,本文提出如下的几种近似方法来获得重力资料的地心纬度。
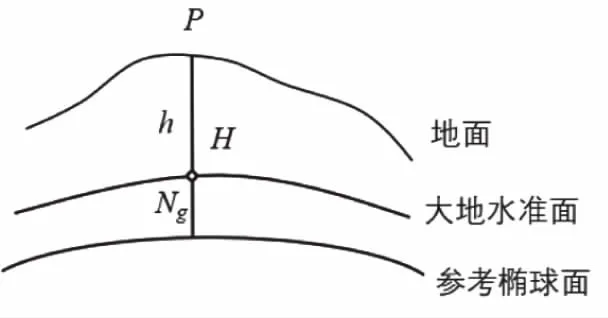
图4 大地高构成图
2.1 借助于已知大地水准面数值模型的转换
根据前述,已知重力测点的高程和大地经纬度信息,并同时能获得测点所在区域的(似)大地水准面数值模型,为计算点位的地心经纬度,可以利用数值内插方法计算出测点的正常高或大地水准面高,再进一步计算出测点的大地高信息,然后利用第1节的严密转换过程计算出测点的地心纬度。
2.2 一步法
参考图1,由于P点的高程与地球半径相比较为一小量,忽略P点的高程,即认为P点位于参考椭球面上,直接利用公式
φ=arctan((1-f)2tanB)
(7)
将大地纬度转换为地心纬度。其中,f为参考椭球的扁率。这种做法对于位于参考椭球面上的测点来说非常简便,然而根据前述的条件,要确定测点是否位于参考椭球面上则是非常困难的,如果测点并不位于参考椭球面上,那么这种做法会带来较大的误差。
2.3 两步法
根据图1,P0点为P点沿参考椭球面法线在椭球面上的投影点,由于大地水准面高相对于地球半径来说是一小量,认为P点的水准高程即P点的大地高,
h≈H
首先借助于上述一步法的公式计算出P0点的地心纬度
φS=arctan((1-f)2tanB)
(8)
即将地球视为半径为R的球体时对应地面点的地心纬度,接着用下式计算出地心纬度
(9)
式中,h为海拔高(到平均海平面的距离),f为参考椭球的扁率,R为地球的平均半径,可取6 371 km。
显然,与一步法相比较,两步法的优点就是顾及了测点的海拔高。
3 数值分析与讨论
3.1 特征区域检查点的计算
为了检验上述三种坐标转换方法的精度,选取了中国范围内五个特征地区的已知重力点共计71点,分别位于西南、东南、中部、西北和东北等地。这些重力点的坐标和其它成果齐全,不仅具有CGCS2000系统的大地坐标,而且具有1985国家高程基准的水准高程信息,其重力系统为2000国家重力基本网系统。其统计信息如表2、表3所示。
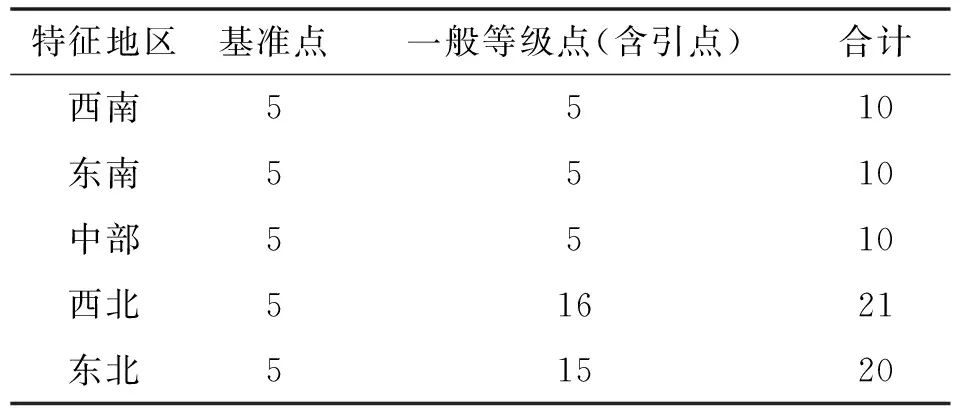
表2 已知重力点数量

表3 区域内重力点的高程特点
在分析过程中,首先利用上述测点的CGCS2000大地坐标计算出其地心纬度的真实值,然后在假设缺乏点位大地高信息的情况下,分别利用上述的两种方法计算出测点的地心纬度,分别与真实值作差比较,并进一步将比较结果转化为对应的地面距离,结果如图5、图6和表4所示。
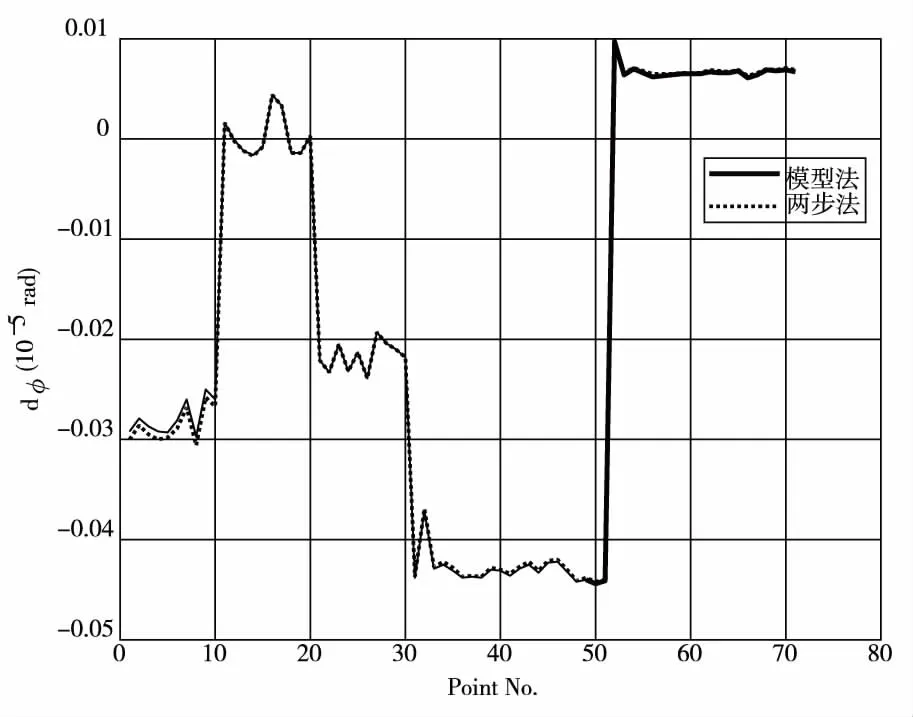
图5 模型法和两步法结果与真实值之差
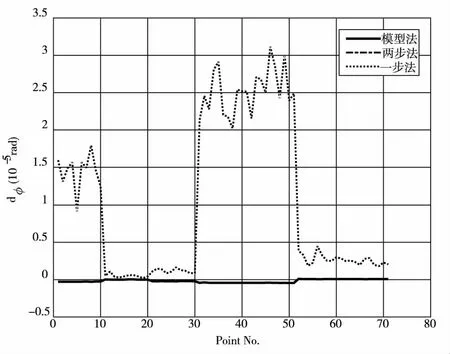
图6 三种方法结果与真实值之差
表4三种方法引起的坐标误差统计/m
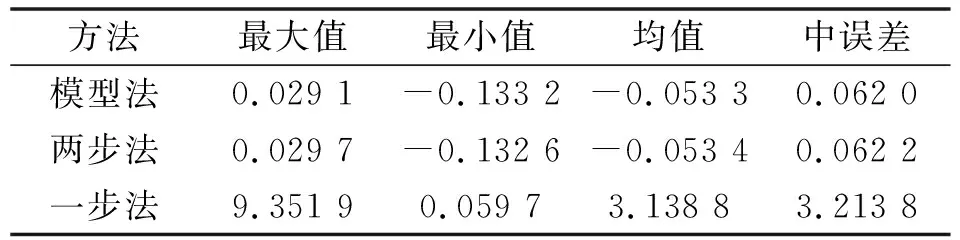
方法最大值最小值均值中误差模型法0.029 1-0.133 2-0.053 30.062 0两步法0.029 7-0.132 6-0.053 40.062 2一步法9.351 90.059 73.138 83.213 8
综合分析图5、图6及表4可知:在不具备测点大地高信息的情况下,利用大地水准面模型法转换得到的地心纬度与真实值的差别最小、其次是两步法的结果、一步法的转换结果与真实值的差别最大;两步法与模型法在转换得到地心纬度的精度上非常接近,因此建议在无法获得可用的大地水准面数值模型的情况下,可用两步法或模型法求取测点的地心纬度。
3.2 重力点的重力值、高程和坐标的精度要求分析
测定重力点的目的在于得到测点的空间异常值。空间异常Δg按下式计算
Δg=g-γ0+0.308 6h
(10)
式(10)中,g为地面上的重力值,h为该点的高程,γ0为正常椭球面上相应点的正常重力值,它可由该点的纬度由正常重力公式算得:
γ0=γα(1+βsin2φ-β1sin22φ)
(11)
由式(10)可以导出空间异常的中误差为:
(12)
由式(11)得:
mγ0=γαβsin2φmφ
(13)
以γα=978 030 mGal和β=0.005 302代入,取sin2φ=1,得:
mγ0=0.025mφ
(14)
式中,mφ为重力点纬度的误差,单位S,算得的mγ0的单位为mGal。将式(14)代入式(12)得到
(15)
式(15)给出了重力点空间异常中误差与观测重力值、点位和高程这三个量的测定误差之间的关系。根据对空间异常的精度要求,按式(15)可对上面三个量的中误差做出一定的安排。考虑到点位误差不能过大,因为点位误差大了必然影响异常值的质量,并顾及到测定重力值、点位和高程各自的困难程度,如在要求空间异常中误差为0.1 mGal时,可按表5进行合理的安排限差。

表5 空间异常误差对坐标限差的要求
结合前一小节及这里得到的限差要求,可知即使在目前对空间异常误差要求严格的情况下,前面三种坐标转换所致误差仍在表5中坐标限差的范围内。这就意味着,即使我们使用转换误差较大的一步法获得测点的地心纬度,仍然不会对最终的空间异常造成较大的影响。然而,随着未来测量手段的进步,空间异常的精度将进一步提高,对坐标误差的限差要求也会更加严格,在此情况下,精度较高而又便利的两步法将是更好的选择。另外,综合表4与表5的结果可知,大地水准面模型法和两步法的转换误差在坐标误差限差中所占比例非常小,而一步法的转换误差在坐标误差限差中所占比例稍大。
4 结 语
本文提出利用已有信息获得地心纬度的几种方法,并通过数值试验对转换方法进行了分析比较,综合分析结果可以得到如下结论:
(1)在大地水准面模型法、两步法和一步法这三种方法中,大地水准面模型法的转换精度最高,其前提是需要转换区域的大地水准面数值模型。两步法的转换精度稍低,但与大地水准面模型法的转换精度非常接近,并且此方法非常直接便利。一步法的精度最低。
(2)在某些对空间异常精度要求严格的情况下,三种方法的转换误差都在坐标误差限差的范围内。其中大地水准面模型法和两步法的转换误差在坐标误差限差中所占比例非常小,而一步法的转换误差在坐标误差限差中所占比例稍大。
(3)在重力资料的处理中若遇到坐标转换问题,我们推荐使用两步法。另外,在计算出地心纬度后,可进一步利用式(6)算出大地水准面高,可得到更加精确的大地高,以及更加精确的地心距,从而使基于地心坐标的重力场计算更加便利。
