InSAR相位解缠质量对比评价分析

刘昱彤，陈星彤，韩 松

(华北理工大学矿业工程学院，河北 唐山 063210)

在摄影测量和现代信息等相关技术飞速发展的基础上，合成孔径雷达干涉测量(InSAR)技术逐渐发展成熟应用起来。InSAR技术突破了SAR成像的局限性，创新性的结合了传统SAR技术和干涉的原理，拓宽了遥感等许多领域的应用前景，具有全天候、全天时优点的同时，还具有高精度的优点，InSAR通过获得相位信息得到更高精度的地面数字高程模型[1]。

InSAR数据的处理过程由于其应用领域的增多变得越来越重要。相位解缠作为处理InSAR数据中的重要步骤，主要兼顾精确性和一致性[2-3]，一直都是专家、学者的重点研究对象。近50年，国内外学者做了大量的分析研究。

1972年第一个求解最小费用算法是Edmonds提出的多项式的时间算法，后来有很多类似方法被提出来，但是仍然没有解决此类问题的强多项式时间算法。Andrea Raith关于求解最小费用流问题，提出了关于双目标整数的两阶段算法,并实现了算法。[4]JIANG Ting-chen基于最小费用流解缠效率低的问题对算法进行了改进。改进思路首先是把干涉相位图划分出的小区域分别进行相位解缠处理；之后再做融合处理，该算法具有可行性[5]。网络流中最为基本的是最小费用流模型，在网络优化中也是最重要的。随着很多基于费用的新函数的提出，该法的发展潜力与日递增。毛志杰等研究了相干系数，在最小费用流算法的基础上进行了算法的改进，改进算法新定义了加权的矩阵。为了减小加权矩阵受幅度的影响，定义了一种新的加权矩阵，从而降低了干涉图相位解缠时由于相干系数较小而影响到的解缠结果。经过处理实验的数据该算法的有效性得到了验证[6]。

目前最小费用流算法已基本成熟。但是最小费用流法相位解缠在确定相干系数等方面有所缺陷，还需要进一步优化其算法。

1 相位解缠的相关理论

1.1 最小费用流法

网络规划的解缠算法最早在90年代末由外国学者提出。基本原理是先寻找缠绕相位与解缠相位差值的全局最优值，使误差达到最小化，再将最小化问题转换成最小费用流问题。使用这种算法处理相关问题，可以得到全局最优的结果，而且相位误差不会在低质量区域范围和高质量区域范围之间流动[7]。在网络规划的最小费用流算法的基础上，缠绕相位与解缠相位之间的关系可表示为

Φ(i,j)=φ(i,j)+2πn

(1)

式中，φ(i,j)∈[-π,π]；n为整数。相位解缠的过程就是从φ(i,j)到Φ(i,j)的过程。

1.2 改进的最小费用流法

怎样才能有效准确的得到加权矩阵一直是在最小费用流算法中困扰众多学者的一个难题。为了减小相干系数较小时对解缠结果的影响，确定新的加权矩阵。改进的最小费用流法相位解缠重点确定了一种不随幅度大小改变的加权矩阵。改进的最小费用流法的相位解缠就是在新的加权矩阵的基础上对相关数据做最小费用流法的相位解缠。

1993年，相干系数这个概念被Prati等提出，它被定义为用来衡量干涉图质量的一种标准[8]。应用时，相干系数中的几何统计由空间统计代替后，这种方法的缺点是空间统计不是常数，随着地面特征的变化而改变，相干系数也会随着变化。针对相干系数的这个缺点，引入噪声模型[9]。随着相干系数大小的变化，噪声模型由不同因素决定着。加性噪声和乘性噪声分别决定着相关系数较小和较大时的噪声模型。而相位展开的效果会在相干系数不是很大时受到干扰。当如果预测的结果出现一定的偏差可能就是源于加性噪声的方差很大。为了减小这种影响，定义加权矩阵为

(2)

式中，μ为功率因子；|ρ|为幅度。

在相位解缠的过程中，首先利用加权矩阵计算出残差值，再通过已成熟的方法计算最小费用流的弧流量，得到相位梯度，进而计算出解缠相位。因此改进的最小费用流法里计算出新的加权矩阵，把乘性噪声源看做相干系数的归一化因子，得到新的加权矩阵，与改进前相比，减少了相干系数对解缠相位的影响。

2 实验数据

本文采用的实验数据是位于陕西省某个矿区的ALOS/PALSAR影像数据，数据类型为JAXA-FBD Level1.1，即经过距离向和方位向压缩的单视复数数据。波束选择L波段因为这个波段不容易被遮挡，可以监测地表的变化。极化方式选择HH。实验范围为110°04′～110°09′E，39°26′～39°31′N的煤矿区。实验选取此项目区的两幅ALOS/PALSAR数据。实验数据原始影像图像灰度值偏低，呈现出颗粒状的斑点噪声，隐藏了影像的细节变化，使影像看起来不清楚，给解译带来了一定的困难。图像的左上角地势起伏较明显，适合做相位解缠的研究。

3 相位解缠实验

InSAR可以对同一地区的单视复数影像进行数据处理，生成该地区数字高程模型(DEM)[10]。由于试验区地表沉降比较复杂，在做InSAR预处理之前要对图像的基线进行简单的估算，分析数据是不是可以做干涉处理。实验区数据两幅图像时间的基线是46 d，空间的基线-291.485 m，临界基线为-6 163.242～6 163.242 m，符合进行InSAR数据处理的条件。从InSAR数据提取DEM的预处理步骤包括4个：复图像配准、干涉图生成、去平地效应、干涉图滤波。数据预处理后得到相应干涉图，再进行相位解缠。

最小费用流法相位解缠结果如图1所示，相位的展开结果基本上可以看出地势的起伏，但是局部展开结果不理想。图上的一些小斑块是相干性差而没有展开相位值的地方。改进最小费用流法相位解缠，解缠结果如图2所示。总的来说，经过改进之后最小费用流法相位解缠结果和之前大致相同，还是存在没有经过解缠处理的图斑。左下角变形较大的区域，可以看出改进的最小费用流法相位解缠比改进之前的解缠效果要好，说明改进是有效果的。

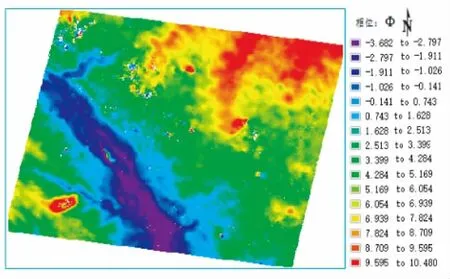
图1 最小费用流法相位解缠图

图2 改进最小费用流法相位展开结果图

4 相位解缠质量评价

本文通过两方面评价指标对比这两种解缠算法解缠效果进行对比分析。

(1)定量统计比较及运算时间对比

对以上两种算法得到的展开结果进行了统计的比较及运算时间对比，如表1所示。

表1 三种相位解缠算法统计分析比较

由表1可知，最小费用流法相位解缠结果的相位差最大为10.480，改进最小费用流法相位解缠结果的相位差最大为8.800。标准差大说明幅值波动大，标准差小说明幅值波动小，因此标准差小说明稳定性好。改进之后的最小费用流法相位解缠结果的标准差为1.483，和改进之前的标准差大小一样，说明改进之后算法解缠的稳定性得到了保持。同样可知，同一运行条件下改进后的展开速度要明显慢于第一种改进前，效率降低。

(2)重建DEM

将两种算法相位解缠之后的结果重建DEM，然后和参考DEM进行对比。参考DEM如图3所示高程值最小为1 138 m，最大为1 381 m，差值为234 m。西北、东南的对角线方向地势最低，两边地势越来越高。

图4为最小费用流法相位解缠重建的DEM，与参考DEM相比，整体地势起伏一致，局部解缠效果不好，存在小斑块。图5为改进最小费用流法相位解缠结果重建的DEM，与参考DEM相比，地势走向大致一致，高程值差值变大。与改进前重建DEM相比，高程值差值变小。

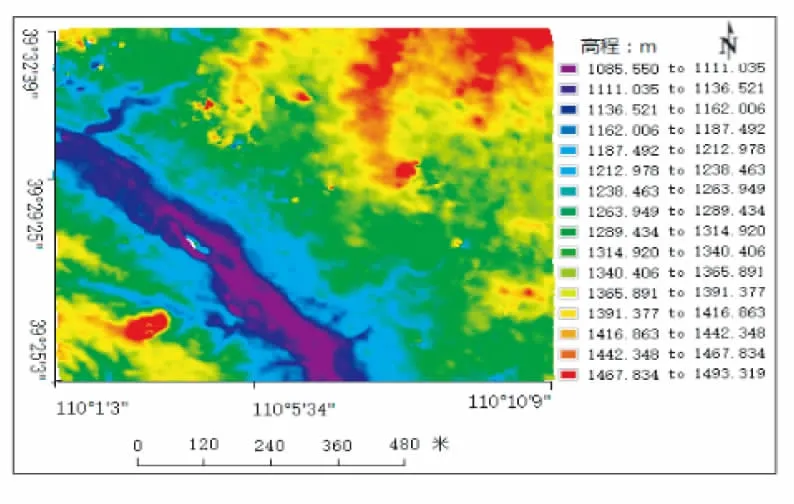
图4 最小费用流法相位解缠重建DEM

图5 改进最小费用流法相位解缠重建DEM

为了精确的比较三种解缠算法重建DEM的结果，选择实测控制点的高程值和对应两种算法解缠结果重建DEM的点的高程值进行对比分析。选取该地区11个水准测量的控制点，得到选取的控制点的高程，如表2所示。

表3为两种算法相位解缠结果重建DEM的高程误差。参考DEM分辨率为90 m，因此重建的DEM的高程差小于90即为合格。两种算法高程误差都小于90，在误差允许范围内。改进最小费用流法相位解缠重建DEM的高程误差比改进之前小，说明改进之后的精度得到了提高。为了直观的对比分析将这三种高程值放在同一幅折线图中，如图6所示。

表2 水准测量控制点的高程值

表3 两种算法相位解缠重建DEM高程误差

图6 三种高程值折线图

由图6可看出，最小费用流法解缠结果重建DEM的高程精度<改进最小费用流法解缠结果重建DEM的高程精度。

综上所述，最小费用流算法的解缠精度不如改进算法后的解缠精度，但解缠的效率要优于改进算法；同时稳定性得到了保持，但解缠的效率慢。所以，精度方面对于改进的方法具有一定的有效性。

5 结 论

相位解缠在整个的InSAR数据处理中是关键一步，相位展开的结果直接影响最后提取DEM的精度。为了精确获得地表细节信息，要研究合适的方法进行相位解缠。针对最小费用流法相位解缠存在的问题，新确定了一个加权矩阵对最小费用流法相位解缠进行了改进，并评价了质量。最终得出结论，改进最小费用流法相位解缠的精度较高，稳定性较好，但是解缠时效较低。因此，解缠时效方面有待进一步改进。