干扰探测一体化信号波形设计与性能仿真

李其虎，王 颖，商开拴

(中国电子科学研究院，北京 100041)

0 引言

随着现代战争的信息化、网络化和智能化水平越来越先进，作战平台工作的电磁环境日益复杂，面临的战场威胁日益增多。为了乙方生存和摧毁敌方威胁目标的需要，未来体系化作战对武器装备的发展越来越呈现出一机多能趋势。目前单一功能、相互独立的机载任务电子系统已越来越难以满足信息化、网络化和智能化战争需要。当前集侦察、干扰、识别、探测于一身，同时结合导航、雷达、通信、对抗于一体的综合任务电子系统备受关注，其中集干扰和探测于一体的共享信号波形可以做到利用强干扰信号进行隐蔽探测，让敌方平台误认为只是在发射单纯的雷达干扰信号而受到广泛研究。文献[1]提出利用单向耦合映象格子构造时空混沌二相序列调制一体化时空混沌二相编码信号波形作为一体化信号。文献[2]基于伪随机信号特点，采用时空混沌系统构造伪随机二相序列实现一体化波形设计。文献[3]针对梳状谱信号的正交特性，分别对探测信号和干扰信息进行调制，得到雷达干扰探测一体化信号波形。文献[4]设计了基于混沌理论的二相编码共享信号，并给出了共享信号的设计思路和优化原则。文献[5]开展了利用噪声跳频、调相信号作为雷达信号的理论推导与仿真。上述信号波形作为雷达信号虽然具有良好的探测性能，但是由于受到发射机的发射脉冲带宽限制，作为干扰信号时，干扰频谱带宽有限，干扰性能较差。因此具有较好探测性能又具备较宽的频谱的共享信号波形是干扰探测一体化信号波形的关键[6-10]。

多载频伪随机相位编码信号波形，因其具有良好的探测性能，而受到广泛研究。但多载频伪随机相位编码信号由于实现的复杂度较高，限制了其在实际工程中的应用。本文通过综合考虑工程实现的复杂性和干扰与探测性能的优良性，采用双载频伪随机二相编码信号作为探测干扰一体化共享信号。由于信号采用相位编码可以使其频谱拓展，使其具备噪声信号特点，而采用两个单一的载频信号，更有利于对回波信号进行处理分析。同时，两个经过伪随机编码调制的双载频信号，可以通过调整载频之间频率间隔实现频带拼接，从而覆盖更宽的频谱范围，噪声信号特性更加明显,且不易被截获。

1 信号特征分析

1.1 探测信号特征

探测信号波形重点关注能否从回波信号通过处理分析获取准确的目标运动信息，包括目标的测量精度和测量分辨力。探测信号的频谱结构决定了该信号测距精度和测距分辨力，因此，为提高对目标作用距离和距离分辨力的探测精度，探测信号应具备较大的频率带宽。探测信号的时域结构决定该信号的测速精度和速度分辨力。因此，为获取较高的测速精度和速度分辨力，要求探测信号具备大的时域宽度。综上可得大的时宽、带宽积是探测信号波形获得高精度测量精度和测量分辨力的前提。因此，为了保证探测系统的测距精度和距离分辨力以及测速精度和速度分辨力，可以独立设计选择探测信号的时宽和频宽等波形参数。

1.2 干扰信号特征

干扰信号根据其使用的方式不同可以分为压制式干扰和欺骗式干扰两大类。压制式干扰主要通过发射大功率宽频的干扰信号，使得对方雷达接收机信干比降低，无法从回波信号中解调检测出目标运动参数。欺骗式干扰是在已知对方雷达的工作频段和具体方位前提下，通过采用模拟发射或转发虚假目标信号方式，包括速度欺骗、距离欺骗、角度欺骗等，增大对方雷达对目标检测的虚警率。压制式干扰相对于欺骗式干扰最大的优点是可以不需要知道对方雷达的具体工作频率和位置，通过选用宽频带的干扰信号，采用大功率发射，对目标实施压制式干扰。

1.3 伪随机二相编码信号特征

伪随机相位编码是采用相位调制编码方式作为探测信号，解决雷达探测能力和距离分辨力之间矛盾，获取较大的时宽、带宽积。伪随机相位编码信号按相位取值数目分类，如果相位只取0和π两个数值，即为二相编码信号。伪随机二相编码信号特征表明该信号呈现出良好的距离分辨力和速度分辨力特性，不存在距离和多普勒耦合问题。此外，相对于线性调频信号，由于相位编码的随机性，该信号具有良好的抗干扰性和低截获性。同时，由于伪随机二相编码的特征主要取决于所采用的二元伪随机序列，因此采用合适二元伪随机编码信号，如巴克序列码、M序列码、L序列码是影响伪随机二相编码信号性能的重要因素。

2 干扰探测一体化波形设计

2.1 信号模型

双载频伪随机二相编码信号区别于伪随机二相编码信号的特点是该信号具有两个载频信号。在信号调制过程时，对每个信号分别进行伪随机编码调制，不同载频所采用的伪随机序列可以相同，也可以不同。根据双载频伪随机二相编码信号的数学定义，其函数表达式可描述为：

s(t)=c1(t)ejα1(t)ej2πf1t+c2(t)ejα2(t)ej2πf2t=
r1(t)ej2πf1t+r2(t)ej2πf2t

(1)

式(9)中，f1和f2为调制载波频率，α1(t)和α2(t)为相位调制信号，c1(t)和c2(t)为实信号调制包络，r1(t)=c1(t)ejφ(t)为复调制包络。为便于数理计算推导，且不失一般性，本文中双载频采用相同的信号包络进行调制，即c1(t)=c2(t)。此时复调制包络r(t)取值可表述为：

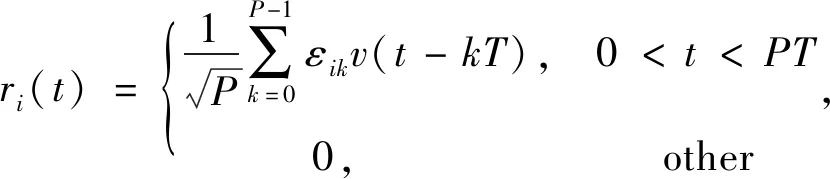
(2)

(3)

式中，εik为产生的伪随机序列，取值为-1或+1，v(t)为子脉冲信号复包络，T为码元宽度,P为双载频的码元数目，则双载频二相编码信号的持续时间为TP。

2.2 模糊函数

模糊函数是对雷达信号特性分析的重要手段，当干扰目标和观测目标之间存在距离和速度的差别时，模糊函数可以定量地表示出干扰目标对观测目标的干扰能力。由于一种信号波形对探测目标的距离分辨力和速度模糊度可以通过该信号的模糊函数表示，因此可以通过模糊函数描述某一信号的探测性能[11]。

基于在上一章节中构建的双载频伪随机二相编码信号模型，信号s(t)的模糊函数χ(τ,ξ)可推导如下：

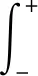
(4)

式(4)中，χao(τ,ξ)和χcs(τ,ξ)表达式分别如式(5)和式(6)所示。

χao(τ,ξ)=[exp(-j2πf1τ)+exp(-j2πf2τ)]·
χ1(τ,ξ)

(5)

χcs(τ,ξ)=exp(-j2πf1τ)χ1(τ,f2-f1+ξ)+
exp(-j2πf2τ)χ1(τ,f1-f2+ξ)

(6)

其中：

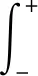
(7)

由二相编码信号模糊函数性质可知：

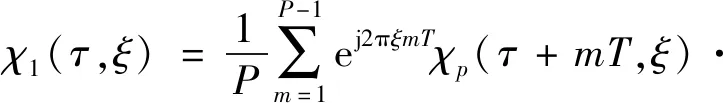
(8)

式(8)中，χp(τ,ξ)表达式如下：

(9)

联合式(4)—式(9)，不难求得双载频伪随机二相编码信号模糊函数χ(τ,ξ)。

2.3 频域特性

当前新体制的抗干扰能力装备都是基于先进的抗干扰算法实现[12-14]。噪声压制干扰是应对先进抗干扰算法的最有效措施，然而完全与噪声特性相符的干扰信号并不存在。干扰信号要有足够的干扰带宽，才能使得更多的干扰信号进入干扰目标的接收机，达到干扰压制效果，因此信号的频谱特征是衡量某一信号的干扰性能的重要指标。根据δ函数的性质，将式(1)改写为：

(10)

根据傅里叶变换性质可得式(11)和式(12)。

根据傅里叶变换性质对式(3)进行频域变换可得：

(11)

同理：

(12)

根据卷积定理，可将式(10)改写为：

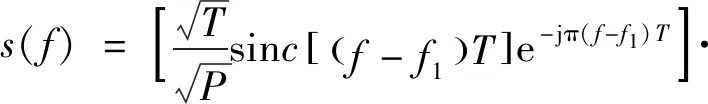
(13)

为便于计算推导，由式(12)可得：

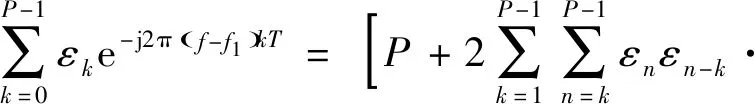
(14)

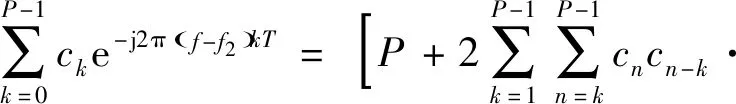
(15)

将式(14)、式(15)带入式(13)可得双载频伪随机相位编码信号频域表达式：

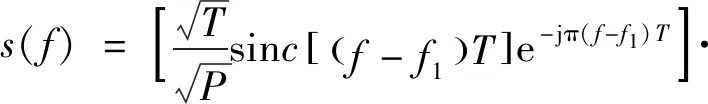
(16)

3 性能仿真与分析

为对基于双载频伪随机二相编码信号波形的探测性能进行验证，对其模糊函数特性进行实验仿真分析，利用31位M序列伪随机码对两个载频进行相位编码，两个载频之间的频率间隔取10 MHz，码元宽度设为0.05 μs进行仿真，结果如图2所示。

从图2中可以看出，模糊函数在时延轴上主峰呈现出良好的尖锐性，主峰附近旁瓣都较低，模糊函数距离分辨力仿真结果表明该信号具有良好的测距能力。模糊函数在多普勒频率轴上的主峰两边出现有两个较高的旁峰，两个旁峰的频率间距为两个载频之间的间隔，幅度为主峰的一半。模糊函数速度分辨力理论仿真结果表明该信号对单目标进行探测时，不会出现速度模糊；在多目标进行探测时，可以通过选择合适的两个载频之间的频率间隔范围，对速度模糊问题进行规避。

为对基于双载频伪随机二相编码信号的干扰性能进行仿真分析。实验分别取码元宽度T在0.4 μs，0.2 μs和0.1 μs时，对信号频谱特性进行仿真。图3为在不同码元宽度下信号的频谱特性图。

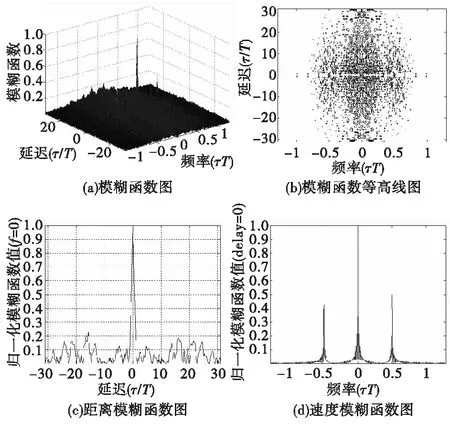
图2 双载频伪随机二相编码信号模糊函数Fig.2 Ambiguity function of dual carrier frequency pseudo-random two-phase coding signal

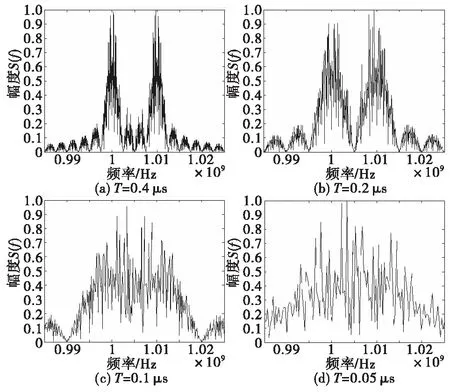
图3 不同码片宽度的信号频谱图Fig.3 Signal spectrum to different chip interval

根据对双载频伪随机二相编码信号频率特性仿真所得的结果，在两个载频频率间隔宽度一定情况下，通过改变码元宽度大小，双载频伪随机二相编码信号呈现出不同的频谱宽度和频谱特性。当码元宽度逐渐减少时，频谱宽度逐渐拓展；当码元宽度减少到0.05 μs时，双载频伪随机二相编码信号覆盖范围内的频率频谱范围将会全部连接上，此时该信号频谱特性与噪声特性趋于一致。上述仿真结果表明双载频伪随机二相编码信号作为干扰信号具有良好的似噪声特性和低截获性能。

4 结论

本文以信息化战争对电子战装备发展趋势为牵引，在综合考虑理论工程实现的复杂性和干扰探测性能的优良性基础上，提出了一种干扰探测一体化信号波形。该波形通过构建基于双载频伪随机二相编码型号模型，理论推导了信号的模糊函数和频谱函数，并对波形特性进行了仿真与分析。实验仿真结果表明，本文所提出的基于双载频伪随机二相编码方式的干扰探测一体化信号波形，不仅在频域上呈现明显的噪声特性，而且在时延轴和多普勒频率轴上还具有较好的距离和速度分辨能力。此外，由于本文所构建的双载频伪随机二相编码信号波形是通过采用两个单独的载频进行调制，因此更便于对回波信号进行分析处理。同时，通过调整信号码元宽度，可使得信号频谱覆盖更宽的频带范围，使得信号噪声特性更加明显。因此，本文所提的干扰探测一体化信号波形理论和仿真分析结果可为干扰探测一体化信号波形的工程化应用提供理论参考。