基于DS理论的遥测定位数据有效性实时判别方法

马方远，杜剑英，申继志，李鹏勃

(中国兵器工业试验测试研究院，陕西 华阴 714200)

0 引言

现阶段，在常规兵器靶场，使用遥测定位数据引导其他外测设备跟踪测试已成常态，由于遥测数据的质量易受弹体姿态、空间电磁环境以及地形地貌变化的影响，遥测数据中往往有些误码，因此，使用遥测定位数据作为其他测试设备的引导源时，需要对遥测定位数据的有效性进行实时判断[1-2]。

目前，遥测定位数据有效性实时判别的通常做法是直接使用包校验技术[3]。对遥测定位数据所在的数据包进行包校验检查，包校验检查通过则认为遥测定位数据有效，否则无效。但由于遥测定位数据所在包的数据长度远大于遥测定位数据的长度，直接使用包校验技术判别遥测定位数据的有效性虽然可以滤除绝大多数的无效数据，但也会带来两个问题：一是过度滤除问题，即遥测定位数据有效，却因其所在数据包其他数据误码导致包校验失败被滤除；二是滤除不干净问题，即遥测定位数据无效，却因包校验规则漏洞包校验通过而未被滤除。

DS证据理论[4-5]是在贝叶斯基础上发展起来的，是对概率论的扩展，证据理论是处理集合的不确定问题，所以使用证据理论时，需将假设的命题与构建的集合之间建立一一对应关系，从而将命题的不确定问题转换为集合的不确定问题来处理。DS理论引入了信任函数，因此可以将遥测定位信息的测试值与理论预测值的误差用信任区间来描述，当误差落在信任区间内时，判断遥测定位数据有效[6]。

1 DS证据理论的基本概念

假设A和B是某一个集合里的两个元素，若A∩B≠∅(∅表示空集)，就称A和B是相容的，假设X的所有可能取值用一个集合U来表示，并且在U内的所有元素之间是互不相容的，就称U是X的识别框架。设U为一个识别框架，函数m:2U→[0,1]并且在满足下列条件时

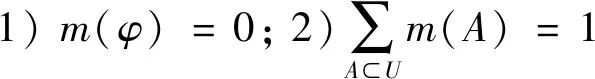
就称m(A)是A的基本概率赋值，即对命题A的基本信任程度可以用m(A)表示。DS证据理论对于任一命题集合还提出了信任函数

A中每个子集的基本信任度之和就是A的信任函数，表示为BEL(A)，它可以表示对A的总信任度。假设把命题A当做识别框架U的一个元素，当m(A)>0时，就称A是信任函数BEL的焦元。

2 遥测定位数据有效性判别方法

设x1(n),x2(n),x3(n)为n时刻飞行器的遥测定位数据中位置、速度、加速度的测试值；y1(n)，y2(n)，y3(n)为n时刻飞行器的理论弹道位置、速度、加速度的数值;z1(n),z2(n),z3(n)为n时刻飞行器的预测位置、速度、加速度值[7]。假设飞行器在时间段[n,n+1]内是匀加速运动，则飞行器的n时刻飞行器的预测位置、速度、加速度[8]可以表示为：

式中，当Δt为遥测定位数据的时间间隔，n=0表示起飞零点，则根据工程实践得知，n≤0时，xi(n)，yi(n)，zi(n)(i=1，2，3)其值都为初始状态值，且此时的值可以认为就是真值，即m(xi(n))，m(yi(n))，m(zi(n))在n≤0时其值都为1，m(A)为A的基本概率赋值。

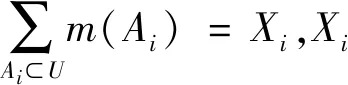
当ai(n)⊄U时，则认为测试值不在合理的范围内，此时的测试值是由遥测误码造成的，应当舍弃，在进行下一时刻预测时，测试值可以按下面公式进行取值：

在这里，位置信息x1(n)使用了x1(n-1)进行预估，而不像速度信息x2(n)与加速度信息x3(n)直接使用了理论值y2(n)，y3(n)代替，主要是考虑到弹箭实际飞行中，飞行轨迹与理论弹道可能有较大的差别，但是速度与加速度差别较小，为了减少迭代计算次数，方便计算效率。

因此，只要确定了一个识别框架U，使得测试值与理论值的误差在识别框架内的概率赋值X合适，就可以使用上述方法对遥测定位数据的有效性进行判断。当ai(n)⊂U时，可以判定此时刻测试值有效，当ai(n)⊄U， 判定此时刻测试值无效。

在实际工程中，识别框架U范围以及概率赋值X的确定，可以通过实时动态的估计测试值与理论值的误差范围与概率[9]，具体实现方法如下：

1) 取一定长度N与一赋值概率X，统计遥测定位信息的测试值与预测值的误差ai(n)，…,ai(n+N)的均方差σ；

2) 设bi=sσ,(s>0)，当满足ai(n)在区间[0,bi]内的概率不小于给定的概率赋值X时，如果s≤3，则令s=3，则区间[0,bi]为判断遥测定位数据有效性的识别框架。

值得注意的是，识别框架[0,bi]的最小上限为测试值与预测值均方差的3σ，是对有效数据的一种保护，即认为误差在3σ以内都是有效数据。另外，X的取值越接近于1，本方法滤除无效遥测定位数据的能力越弱；X的取值过小，本方法将产生很多误滤除，正常的遥测定位数据也很难通过有效性判别；N的取值越大，本方法滤除无效遥测定位数据的能力越强，但是延时输出就越长。在实际工程应用中，X可取0.8～0.95之间，N可以根据遥测定位数据的周期，统筹均衡样本量的数量与延时输出，保证不影响需要引导跟踪的设备跟踪测试[10]。

3 试验验证

为了充分验证算法的效率，本文的试验验证数据来自于某型号靶场试验的遥测数据中导航计算机导航数据发射坐标系下的射程X，其数据周期为12 ms，最大射程为495 km，飞行过程386.64 s，共有3 223个点的数据，由图1可以看出，且遥测数据的质量较差，误码较高。

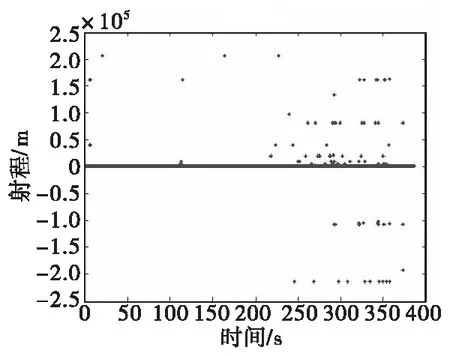
图1 某试验遥测数据中射程-时间数据曲线Fig.1 Range-time data curve in a test telemetry data

直接采用包校验技术对遥测定位数据有效性进行判别(此数据的包校验为8位校验和)，判别结果如图2所示。绝大部分的遥测误码已经滤除干净，但仍有两个无效遥测定位数据未被滤除，所剩共计2 988个有效数据。

图2 包校验后剩余的数据曲线Fig.2 Data curve remaining after package verification

采用连续200个点(2.4 s延时输出)的测试值与预测值进行动态误差统计，统计并计算概率X为90%时的最小识别框架U的上下限。采用本文方法对下一个测试值进行有效性判断，判断结果如图3所示。遥测误码造成的不正常数据已经滤除干净，所剩共计3 029个点的有效数据，与图2比较可以看出使用数据包包校验技术，多滤除了41个有效遥测定位数据。

图3 经过有效性判别后剩余数据曲线Fig.3 Residual data curve after validity discrimination

采用连续200个点(2.4 s延时输出)的测试值与预测值进行动态误差统计，统计并计算概率X为90%时的最小识别框架U的上下限。采用本文方法对下一个测试值进行有效性判断，并使用预测值代替被剔除的无效遥测定位数据，补全引导数据后的数据如图4。

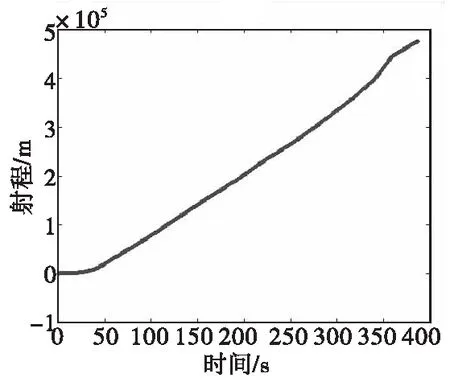
图4 补全后的引导数据Fig.4 Guidance data after completion

4 结论

本文提出了基于DS证据理论的遥测定位数据有效性实时判别方法，该方法利用了遥测数据中的定位数据的位置、速度、加速度信息和理论弹道位置、速度、加速度信息，预测遥测定位数据的合理范围，使用DS证据理论原理，直接判断遥测定位数据的有效性，因此避免了常规使用数据包包校验技术带来的遥测定位数据过度滤除问题。试验验证表明，基于DS证据理论的遥测定位数据有效性判别方法，可以更有效地滤除遥测定位数据中的无效数据。