一种用于引导的遥测定位信息外推算法*

2020-09-01马方远杜剑英李鹏勃申晓敏

弹箭与制导学报 2020年2期

马方远,杜剑英,李鹏勃,申晓敏

(中国兵器工业试验测试研究院, 陕西华阴 714200)

0 引言

在常规武器试验靶场,雷达/光电经纬仪等外测设备在没有靶场网络覆盖的试验弹道航落区进行试验测试时,往往不能独立完成测试,需要其他设备对其进行引导测试。弹载遥测定位信息具有精度高、误差稳定,不受天气影响等特点[1],使用该信息引导并进行试验测试,不失为一种有效的方法。但是传统的遥测测量是一种准实时的测试过程,遥测定位数据到达被引导设备时有一定的时间滞后,直接使用遥测定位信息进行引导,引导数据误差大,不能满足雷达/光电经纬仪近距离跟踪目标,因此这就需要对遥测测试数据链路的时延进行估计,用一种有效的定位数据外推方法,提高引导数据的精度。

1 遥测定位数据外推算法

首先假设遥测定位信息为真值,即遥测测试值为真值,其次假设遥测定位信息在局部时间范围内为线性关系,则遥测定位数据的外推方法可按图1设计,通过估计遥测数据处理链路延时t,对于Tn时刻的遥测定位数据进行时间补偿与权值补偿后外推Tn+t时刻的位置,当Tn+k时刻到来时,使Tn+t时刻在区间[Tn,Tn+k]内,使用Tn+k时刻与Tn时刻的遥测定位信息求出Tn+t时刻的理论真值,对Tn时刻的外推值进行精度评估,修正外推系统的外推权值,从而消除外推模型的系统误差。

图1 遥测定位数据外推算法设计

1.1 外推模型建立

遥测定位信息包括时间、位置、速度等信息,因此可以通过对遥测数据链路的延时进行估计,使用速度信息来对定位信息进行外推。假设X(k)为k时刻遥测定位数据测试值,遥测数据链路延时为Δt,经处理后引导数据在t时刻到达被引导设备,X(t)为t时刻遥测定位信息的预测理论值,Z(t)为t时刻外推位置,则外推模型为：

(1)

式中:V(k)为k时刻遥测定位信息速度测试值;H(t)为t时刻外推系统权值,在实际工程中,一般可以取H(0)=1;W(t)为t时刻外推系统噪声，取W(t)=0。

由式(1)可知,只要确定遥测数据通信链路延时的估计与外推系统权值的确定,就可以完成遥测定位信息的外推。

1.2 遥测数据链路延时估计

遥测数据链路[2]主要是指遥测定位信息从遥测采编器采集到最终转换为引导数据到达引导设备之间的通信链路。整个数据网络的延时主要由定位数据包采集耗时、遥测信号的空间耗时、遥测数据的解帧耗时、遥测数据的发包耗时、遥测数据的数据处理耗时以及引导数据网络传输耗时组成。遥测数据的解帧耗时、遥测数据处理耗时、引导数据网络传输耗时都在1 ms以内,可以忽略其影响,则遥测数据链路延时可以按照式(2)进行计算:

Δt=T1+T2+T3

(2)

式中:Δt为整个引导链路的数据延时;T1为遥测定位信息数据包采集耗时;T2为遥测数据的空间传输耗时;T3为遥测数据的发包耗时。

遥测定位信息数据包一般都采用422串口进行传输,遥测采编器实时或准实时采集422串口上的数据,其传输耗时可用式(3)计算。

T1=s1×b/m

(3)

式中:s1为GPS/BD数据包包长,单位:Byte;b为串口输出一个字的占位,单位:bit;m为串口输出波特率,单位:bit/s。

遥测数据的空间传输耗时,与目标距离遥测地面站的距离有关[3],计算公式为:

T2=s2/c

(4)

式中:s2为目标距离遥测地面站的距离,单位:m;c为电磁波在空气中的传播速度,单位:m/s。

遥测数据发包耗时主要是指遥测地面站实时解调遥测信号,使用UDP协议网内发送遥测数据包的时间间隔。它与遥测数据码速率与遥测解调器发包大小有关,可按下面公式计算。

T3=s3×8/m

(5)

式中:s3为遥测解调器的发包内存大小,单位:Byte;m为遥测数据的码速率,单位:bit/s。

1.3 权值的确定

进行权值修正时,首先假设定位数据的测试值为理论真值,则按照上述方法得到的外推值可以用后面测试值进行精度评估,修正外推算法中权值,具体计算过程为：

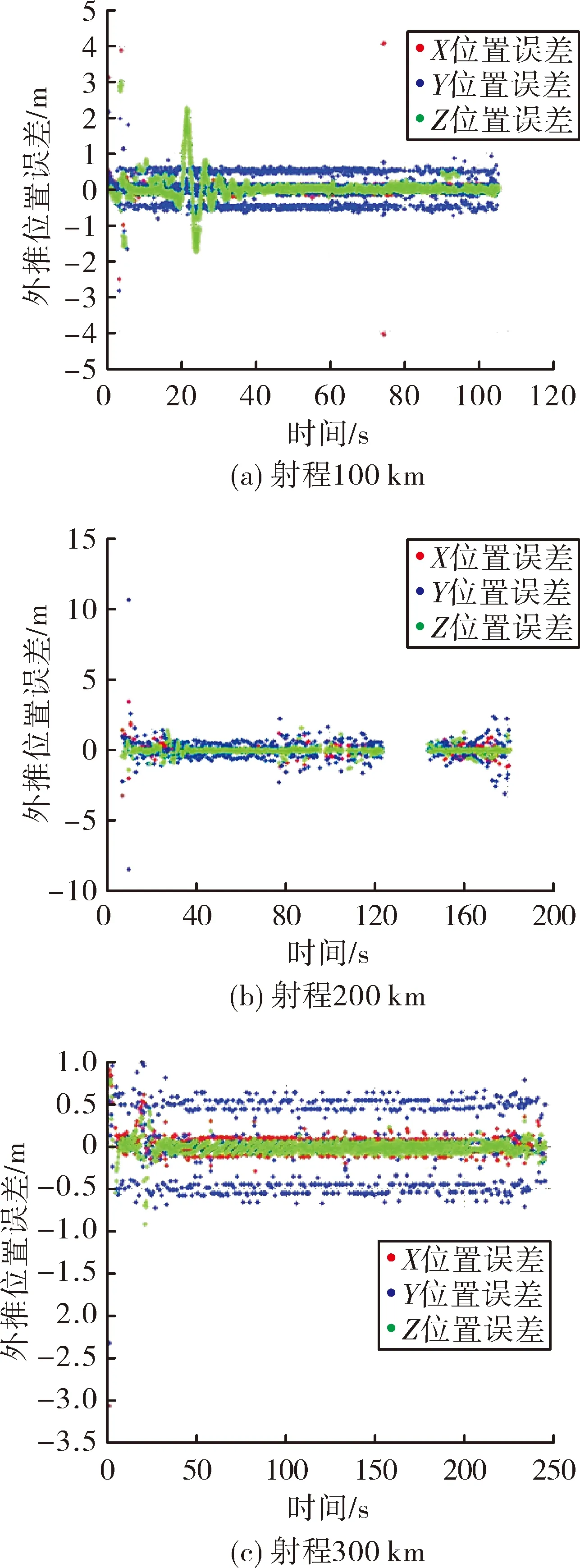
H(t)=((X(k+m)-X(k))×Δt/m+
X(k))/X(k)+V(k)×Δt,k<Δt

(6)

式中:m为从k时刻到t时刻后最接近t时刻的GPS/BD数据道路时间间隔,单位:s;X(k+m)为k+m时刻GPS/BD数据的测试值,单位:m;由于X(k+m)是未来的遥测定位数据测试值,所以假设H(t)在一段时间内稳定,则将式(6)改写为:

H(t)=((X(k)-X(k-m))×Δt/m+
X(k-m))/X(k-m)+V(k-m)×Δt
k<Δt

(7)

2 外推算法理论精度验证

遥测定位信息外推算法理论精度的验证,可以通过将试验项目中的遥测定位数据与按文中方法得到的引导数据按照GPS绝对时间对齐,换算到发射坐标系下[4]进行三轴向数据的精度对比进行,下面通过对靶场某100 km、200 km、300 km试验项目遥测数据进行分析,验证文中外推算法精度。

如图2所示，当遥测数据稳定后,遥测定位数据的外推值与遥测定位数据的测试值之间的三轴最大误差绝大时候都小于1 m。经过误差分析[5]可以得到,100 km试验中遥测定位信息的外推数据与遥测定位信息的平均误差为:E(ΔX)=0.007 m,E(ΔY)=0.002 m,E(ΔZ)=0.011 m,误差均方差为:σX=0.158 m,σY=0.222 m,σZ=0.364 m;200 km试验中遥测定位信息的外推数据与遥测定位信息的平均误差为:E(ΔX)=0.036 m,E(ΔY)=0.021,E(ΔZ)=-0.028 m,误差均方差:σX=0.125 m,σY=0.271 m,σZ=0.041 m;300 km试验中遥测定位信息的外推数据与遥测定位信息的平均误差为:E(ΔX)=0.010 m,E(ΔY)=0.007 m,E(ΔZ)=-0.011 m,误差均方差：σX=0.157 m,σY=0.430 m,σZ=0.106 m。

图2 某试验遥测定位信息外推算法误差分析

3 外推算法精度靶场试验验证

遥测定位信息外推算法精度的靶场试验验证,可以通过对比试验项目中布设在同一位置的两台雷达的天线跟踪角度,一台雷达使用自主跟踪模式,一台雷达使用遥测定位信息引导模式。下面通过对靶场某100 km、200 km、300 km试验项目雷达天线跟踪角度信息进行分析,验证文中外推方法精度。

如图3所示试验雷达作用距离为100 km，当飞行试验稳定后,雷达天线自跟踪角度与遥测定位信息引导雷达天线跟踪角度误差绝大部分不超过0.1°。经过误差分析可以得到,100 km试验中雷达天线自跟踪角度与遥测定位信息引导雷达天线跟踪角度平均误差为:方位E(Δθ)=-0.03°,俯仰E(Δγ)=0.051°,误差均方差为:方位σθ=-0.091°,俯仰σγ=0.028°;200 km试验中遥测定位信息的外推数据与遥测定位信息的平均误差为:方位E(Δθ)=-0.03°,俯仰E(Δγ)=0.051°,误差均方差为:方位σθ=-0.052°,俯仰σγ=0.028°;300 km试验中遥测定位信息的外推数据与遥测定位信息的平均误差为:方位E(Δθ)=-0.006°,俯仰E(Δγ)=0.025°,误差均方差为:方位σθ=-0.008°,俯仰σγ=0.005°。