夯实基础 建构体系

潘正刚

[摘要]尺规作图是几何教学的重要组成部分，是作图能力的集中体现，是理性思维的重要代表。设计以夯实基础、建构体系为目标的尺规作图专题复习课，能让学生在问题解决中熟悉五种基本作图方法，能发展学生的数学学科核心素养。

[关键词]尺规作图;理性思维;教学设计

[中图分类号]G633.6[文献标识码]A [文章编号]1674-6058（2020）08-0008-03

数学学科核心素养是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现。教师为未来而教，学生为未来而学。数学教学也要跟随时代的进展而变化，其方法便是“精中求简”。精选必备知识、培养关键能力。尺规作图是平面几何的核心内容。但是其内容众多，部分作图难度较大。《义务教育数学课程标准（2011年版）》一方面保持了尺规作图在平面几何中的重要地位;另一方面精选了内容，保留其精华。北师大版教材，以探索基本图形的性质和定理为主线编排几何的内容，尺规作图的内容分散于各章节之中。教学中，教师普遍重视性质和定理的推理论证，对尺规作图存在不同程度的忽视情况。因此，有必要在七年级下册，以整体视角设计以尺规作图为主题的复习课，以兴趣为引领、问题为驱动，让学生形成对相关内容的新理解，建构尺规作图的体系。

一、教材分析

在北师大版教材中，学生分别在七年级上册第四章《基本平面图形》中学习用尺规作线段，在七年级下册第二章《相交线与平行线》中学习用尺规作角，在第四章《三角形》中學习用尺规作三角形，在第五章《生活中的轴对称》中学习作已知线段的垂直平分线和作已知角的平分线。

二、学情分析

学生掌握了四种基本作图的方法，了解作图的原理，并初步应用基本尺规作图。但由于知识比较分散，学生普遍还未将这部分知识纳入自己的知识体系，欠缺综合运用知识的能力。

三、教学目标

1.复习四种基本尺规作图的方法和原理，应用探索第五种基本作图——过一点作已知直线的垂线，初步建构尺规作图知识体系;

2.在问题解决中，联系已有几何知识，灵活运用基本作图方法构造图形，积累操作经验，发展理性思维。

四、教学设计

（一）创设情境，赏尺规之美

《几何原本》是由2000多年前的古希腊数学家欧几里得所著的不朽之作，书中公理化的思想方法成为后世建立知识体系的典范。书中收录了天文学家、数学家伊诺皮迪斯所提出的两个命题：给定直线外一点求作直线的垂线;求作一角等于已知角。明确提出只准使用直尺和圆规两种工具。从此尺规作图逐渐成为一种公约。在古代，数学家利用尺规作图解决了各种难题。如图1，高斯证明了尺规作图可以作出正十七边形;在现代，人们借鉴尺规作图进行平面设计，如图2为苹果公司的Logo。

[设计意图]聆听数学故事，欣赏平面设计，让学生感受尺规作图之关，体会尺规作图所蕴藏的数学文化。此环节既展现数学现实化的特点，又发挥数学教育化的功能，学生从感性的角度再度认识尺规作图，激发学习兴趣。

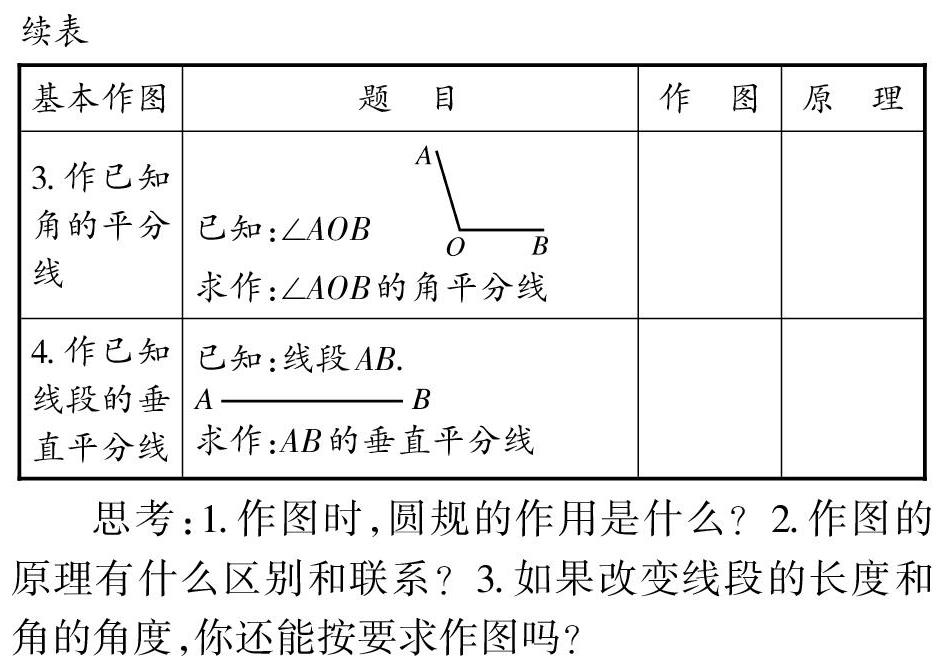
（二）实践操作，悟尺规之理

思考：1.作图时，圆规的作用是什么？2.作图的原理有什么区别和联系？3.如果改变线段的长度和角的角度，你还能按要求作图吗？

[设计意图]由于学习时间跨度较长，不少学生对于尺规作图的记忆是模糊的、零散的。故设计从基础开始，有序回顾四种基本作图，在作图中复习方法，在说理中训练逻辑推理的能力，在操作中体会圆规的作用是截取相等的线段，在对比、反思中发现以其作图原理都可以用全等三角形的判定定理“SSS”来解释，从而建立起四种基本作图的內在联系。在操作性教学活动中，教师的现场示范更有利于学生熟练掌握作图步骤。因此建议教师采用亲自作图演示为主、几何画板动态演示为辅的教学方式。部分学生对于尺规作图不能使用刻度尺和量角器难以理解，这成为学习道路上的拦路石。设计此教学环节的目的正是为了让学生了解尺规作图的应用价值，体会尺规作图的理性思维。笔者还希望帮助学生解开一个困惑：为什么在作图中不能测量长度和角度？如果仅仅说这是尺规作图的规则，很难让学生释怀。经历充分操作、深入交流，从全等三角形的证明过程回到尺规作图的每一个步骤，引导学生思考严谨的演绎推理可以解决由操作、测量误差等导致的不确定性。

（三）问题驱动，促尺规之用

[设计意图]过一点作已知直线的垂线是第五个基本作图。对学生而言，这是一个具有应用意义的新问题。该作图以例题形式出现，作为基本作图的应用，学生在操作中进一步体会直尺和圆规的功能性作用，在说理中体会类比、转化的思想，促进应用基本作图的意识的形成。

[设计意图]这道开放性题目让学生继续积累将复杂作图转化为基本作图的经验。较多学生采用作角的平分线和线段的垂直平分线的方法来完成作图，不少学生欠缺作等线段和等角来解决问题的直觉。本题提出一题三解的要求，旨在拓展学生思维广度，让学生展开丰富联想，进一步促进学生应用各种基本作图的意识。教师在讲解申要提高要求，引导学生联系等腰三角形来陈述作图原理，帮助学生找到思维起点，培养逻辑推理能力。

[例3]用尺规作一个30°的角（保留作图痕迹，不写作法）。

[设计意图]本题旨在挖掘思维的深度，展现学生的知识层次和能力水平。若学生无法联想到熟悉的几何模型，便难以建立与30°相关的图形联系。复杂作图，不是基本知识的简单堆砌，需要相关几何图形和定理的衔接，综合运用几何知识，模块化建立几何模型，再以基本作图为工具解决问题。教学申，教师要力图让学生呈现出思维过程的不同层面：一是从数的层

（四）总结归纳，悟尺规之道

师生共同小结：（1）基本作图有哪些？（2）课堂中所作的图形有什么特点？（3）请举例说明，在作图过程中体会到什么数学思想方法？

[设计意图]平行线是七年级下册的重要內容，本题将平行线的判定和基本尺规作图联系在一起。此题有多种巧妙的作图法。直接法：作內错角相等、同位角相等;间接法：作垂直于同一条直线的两直线、作全等三角形、先做角平分线后作等腰三角形、作正方形和作菱形。学生要找到思维起点，即回到平行线的判定定理，联想几何模型，再转化为基本作图来解决问题。

五、教学反思

尺规作图是初中数学难得的操作性教学内容，其源于操作，植根于结合图形性质的逻辑推理。即是联系、重构、内化几何知识的教学素材，发展学生应用意识、促进学生体悟数学思想方法、培育学生核心素养的教学载体。本课设计基于基本作图的内在关联、复杂作图的分析建构，力图夯实基础并建立与尺规作图相关的知识结构，并将其融合于平面几何的知识体系之中。本课例设计指向“问题解决”，选取基础但能一题多解的例题。在教学中充分发挥学生的主观能动性，关注基础知识的应用，启迪学生的发散性思维，促进学生领悟类比、化归、数形结合等数学思想方法，提升学生应用数学知识解决实际问题的能力。