赣南花岗岩残积土路基变形规律的数值仿真

2020-03-30费伦林纪更占

公路交通科技 2020年3期

费伦林，纪更占，林盛

(1.江西省高速公路投资集团有限责任公司，江西南昌 330025； 2.同济大学道路与交通工程教育部重点实验室，上海 201804)

0 引言

花岗岩在我国分布广泛，约占国土面积的9%，尤其在东南沿海地区分布更为广泛[1]。因花岗岩节理发育，风化作用可沿节理向内部蔓延，形成厚层、巨厚层的红色风化壳，从而构成了赣南乃至我国东南部的特色花岗岩地貌[2]。花岗岩红色风化壳的上部土层就是花岗岩残积土，是花岗岩经物理风化和化学风化后残留在原地的碎屑物，是一种结构性很强的特殊土，具卸荷崩解、遇水软化、液限高等特性，在南方多雨地区表现尤为突出。按照路基设计标准，花岗岩残积土并不是一种理想的路基填料。但随着经济发展，人们出行的交通需求日益增长，各省公路建设逐步向山区推进，由于道路线型要求，高填深挖现象难以避免，土石方工程浩大。基于工程进度、经济成本和环境保护等因素考虑，必须充分利用沿线花岗岩残积土。

花岗岩残积土天然含水率高，在潮湿多雨的南方地区，很难通过晾晒降低至最佳含水率附近。实际施工过程中，填料往往在天然含水率下直接进行压实填筑，路基压实度难以达到规范要求。填筑后，路基工后变形可能较大，容易引起路基路面开裂，不利于车辆安全稳定的运行。周德泉通过室内压缩试验和模型槽载荷试验，研究花岗岩残积土的压缩变形和湿化变形特性[3]。李志勇[4]和周援衡[5]分别采用动三轴试验、数值模拟来探究风化花岗岩的动力变形特性。姚裕春[6]和鲍晓东[7]则通过路基离心模型试验研究风化花岗岩的固结变形特性。同时，也有学者通过修筑现场试验段，并进行长期沉降观测以分析花岗岩残积土的变形特性[8-9]。但总体来说，路基填料压实状态对花岗岩残积土路基变形的影响仍不明确。此外，饱和土路基的沉降计算与预估已经形成比较系统的计算理论和方法[10-12]，但路基填料一般属于非饱和土，应当考虑利用非饱和土力学理论对花岗岩残积土路基的变形规律进行分析。

鉴于此，本研究采用Geostudio岩土有限元分析软件，基于非饱和土流固耦合理论，考虑路基填筑过程中由于不同的含水率和压实度构成的压实状态，以及不同的填筑高度和施工工序对花岗岩残积土路基变形的影响。

1 非饱和土流固耦合理论

耦合是指考虑不同流体流动与土结构平衡的相互作用，即连续方程与平衡方程的解[13]，本研究具体指渗流场与应力场方程的解。通过对平衡方程和连续方程及其对应初始和边界条件的求解，即可得到耦合方程的解。

1.1 平衡方程

非饱和土的应力应变增量关系可表示为：

(1)

(2)

(3)

(4)

(5)

(6)

式中，εx，εy，εz为x，y，z方向的正应变；γ为剪应变；σx，σy，σz为x，y，z方向的总法向应力；τxy，τxz，τzy为x，y，z方向的总法向应力；μa为孔隙气压力；μw为孔隙水压力；E，G为土体结构的弹性模量和剪切模量；H为由基质吸力(μa-μw)引起的非饱和土结构的模量；μ为泊松比。

在二维问题中，其应力应变方式可表示为：

(7)

非饱和土的应力应变增量关系也可表示为：

Δσ=KΔε-KmH(μa-μw)+{Δμa},

(8)

式中Δε为应变增量。

根据虚功原理，建立有限元平衡方程，当只有外部点荷载F被施加时，虚功方程可表示为：

(9)

式中，δ*为虚位移；ε*为虚应变；σ为内应力；F为外部点荷载。

求解可得：

∑BTDBΔδ+∑BTD·mH〈N〉Δuw=∑F，

(10)

式中，N为形函数行矢量；B为刚度矩阵；D为排水本构矩阵。

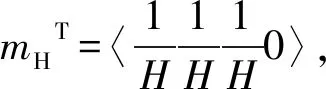
KΔδ+LdΔuw=ΔF，

(11)

式中，K为刚度矩阵；Ld为耦合矩阵；Δδ为增量位移矢量；Δuw为增量孔隙水压力矢量。

1.2 渗流方程

Darcy定律同样适用于非饱和土中水的流动[13]，也即：

(12)

(13)

式中，vx，vy为x和y方向的渗流速度；h为总水头；kx，ky为土体在x，y方向的渗透系数。

假设土骨架不变形，水为不可压缩流体，不考虑生物化学作用对渗流的影响，根据质量守恒原理，非饱和土二维非稳定流情况下，流入流出单元的水量变化率等于该单元内水量随时间的变化率，由此可以得到的连续方程为：

(14)

可以得出非饱和土渗流的基本微分方程：

(15)

式中，θω为土的体积含水率；t为时间。

(16)

使用有限元近似法，则方程变为：

(17)

(18)

式中，B为梯度矩阵；Kw为渗透系数矩阵；Kf为单元刚度矩阵；N为形函数行矢量；MN为质量矩阵；Lf为渗流耦合矩阵；mT为各向同性单元张量〈1110〉；δ为节点位移；Q为边界节点的渗流。

2 数值模型构建

2.1 模型尺寸及边界条件

模型几何形状和网格划分如图1所示，地基网格尺寸为2 m × 2 m；路堤网格尺寸为宽×高=0.5 m×1 m。路基顶面宽为22 m。填筑高度分别设定为5，10，15，21 m和25 m。根据高度变化设置3级边坡：路基顶面以下8 m范围内，坡率为1∶1.5，台阶宽度为2 m；路基顶面以下8～16 m范围内，坡率为1∶1.75，台阶宽度为2 m；路基顶面16 m以下，坡率为1∶2。地基设定为均质，计算宽度取80 m、深度取20 m，起始地下水位设在地基顶面以下8 m处。路堤填料为压实花岗岩残积土，路床填料为水泥改良花岗岩残积土。路基顶部由于覆盖了沥青混凝土路面，假定为不透水，仅在坡面排水。

图1 数值分析模型(单位:m)Fig.1 Numerical analysis model(unit:m)

2.2 材料参数

土样取自江西赣州某高速公路沿线。路面结构设置面层、基层、底基层，各层厚度及材料参数参考卢正[14]等人的研究结果；地基土视为各向同性的线弹性材料，重度18.5 kN/m3，变形模量18 MPa，泊松比0.3；水泥改良花岗岩残积土，视为各向同性的线弹性材料，压实度96%，重度17.3 kN/m3,变形模量70 MPa，泊松比0.3；花岗岩残积土采用弹塑性模型，变形模量通过常规固结试验中压缩模量转换得到[15]。考虑不同压实度和初始含水率的影响，室内试验在3种压实度和3种初始含水率共9种工况下进行。其中，初始含水率的取值分别对应击实最佳含水率(14.8%)、最大承载比含水率(16.6%)和天然含水率(20.2%)。试验得到不同压实状态的花岗岩残积土材料参数如表1和表2所示。试验过程严格遵照《公路土工试验规程(JTG E40—2007)》[16]的有关规定，其中，压缩模量通过T 0137单轴固结仪法得到，进而计算变形模量；黏聚力和内摩擦角通过T 0142直剪试验得到；基质吸力根据ASTM滤纸法[17]测得。

表1 不同压实状态花岗岩残积土的计算参数Tab.1 Calculation parameters of granite residual soil in different compaction states

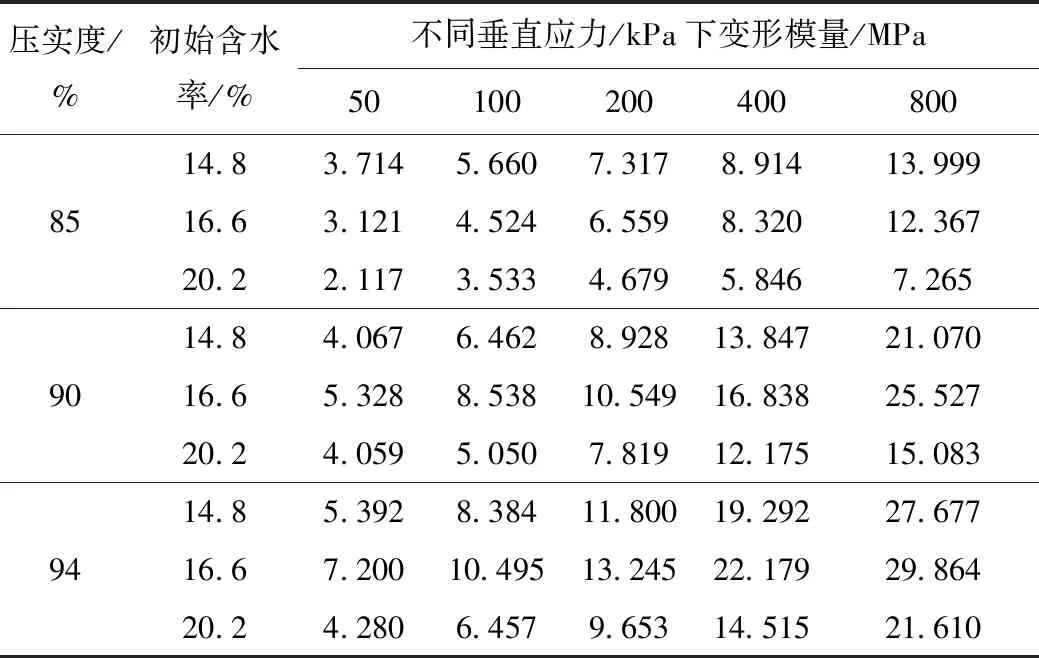
表2 不同压实状态花岗岩残积土的变形模量Tab.2 Deformation moduli of granite residual soil in different compaction states

图2 不同压实度下花岗岩残积土土水特征曲线与渗透系数Fig.2 Soil-water characteristic curves and penetrating parameters of granite residual soil with different compactnesses

3种不同压实度下花岗岩残积土的土水特征曲线如图2(a)所示，曲线根据ASTM滤纸法[17]测得数据点，并利用Van Genuchten模型[18]拟合得到。土样压实度为85%,90%和94%时，根据《公路土工试验规程(JTG E40—2007)》[16]T 0130规定的变水头渗透试验，确定其饱和渗透系数分别为1.251×10-3，6.797×10-4,1.411×10-4m/d。采用Fredlund & Xing模型[19]对花岗岩残积土的非饱和渗透系数进行预测，不同压实度下渗透系数随基质吸力变化曲线如图2(b)所示。

2.3 荷载条件

以填方自重作为荷载，填筑速率按以下情况进行计算：一次性填筑，填筑速率为0.5 m/d，且路基填筑完成后直接铺筑路面；分阶段填筑，填筑速率分别为0.25，0.5，1.0 m/d，且每填筑5 m 后进行20 d的施工间歇期，路基填筑完成后，经历90 d的沉降稳定期，再铺筑路面。现场实际填筑速率为0.5 m/d，同时人为假定0.25 m/d和1.0 m/d的填筑速率作为对照组，数值模拟中通过设置每层填土的施工天数来实现。施工进度如图3所示。

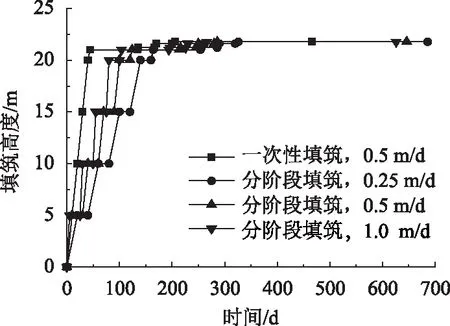
图3 路基施工进度Fig.3 Subgrade construction process

2.4 模型验证

为验证所建数值模型的可靠性，将工程实际监测数据与数值计算结果进行对比分析。依托工程为典型花岗岩残积土路基，填筑高度21 m，路基宽度22 m，在原地基顶面以下0.5 m共埋设6个智能沉降计，水平方向距离坡脚2,8,18,24,32,40 m。工后实际监测结果与模型计算结果如图4所示。

图4 地基工后变形监测值与计算值对比Fig.4 Comparison of post construction deformations of foundation between monitored value and calculated value

由图4可知，地基工后变形的数值计算结果与实际监测结果变化趋势相同，变形量随时间在初始阶段随时间曲线增长，最终趋于稳定。由于监测时间较短，地基尚未达到稳定阶段，因此地基工后实际变形量呈逐渐增大的趋势，但增长速率逐渐减小。利用双曲线模型[20]拟合实测数据，据此计算的地基工后变形最终值与数据模型计算结果较为吻合。以距路基边坡40 m处的监测点为例，数值计算工后最终变形量为8.14 cm，根据实测数据预测最终变形量为8.12 cm，相差0.02 cm。由此可以说明本研究采用的数值计算理论和参数，能够较好地反映出地基变形特性，间接表明模型计算结果能反应整个路基的变形规律。

3 路基变形影响因素分析

3.1 路基压实状态的影响

路基填筑高度为21 m，施工工序为速率0.5 m/d的分阶段填筑。路面铺筑完成后1 080 d，不同初始状态下，花岗岩残积土路基总变形如图5所示。可以看出，在压实度为85%时，路基总变形随初始含水率的增大而增大；在压实度为90%和94%时，随初始含水率的增加呈现先减小后增大的趋势，在最大承载比含水率下取得最小值。

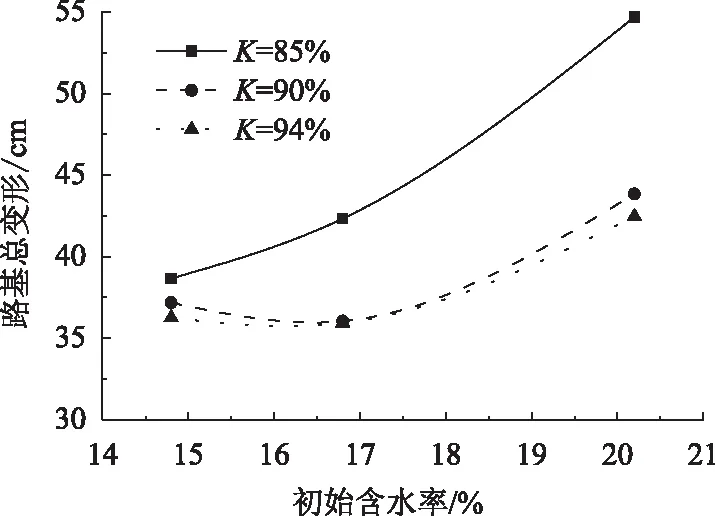
图5 不同初始状态下花岗岩残积土路基总变形Fig.5 Subgrade total deformation of granite residual soil subgrade in different initial states

路面铺筑完成后1 080 d，对不同状态下地基工后变形和路堤工后压缩变形进行分析，如图6所示。其中，地基的工后变形为地基顶面中心点的变形，路堤工后压缩变形为路基顶面中心点变形减去地基顶面中心点变形。可见，对地基而言，压实度的提高导致花岗岩残积土的重度提升，工后变形随之提高；对路堤而言，变形模量随含水率的变化亦较为显著，最大承载比含水率处进行充分压实可获得较小的压缩变形。

图6 不同初始状态下花岗岩残积土路基工后变形Fig.6 Post construction deformation of granite residual soil subgrade in different initial states

根据室内试验结果可知(见表2)，85%压实度下，土体变形模量随初始含水率的增大而减小；而90%和94%压实度下，土体变形模量随初始含水率的增大呈先增大后减小的趋势，在最大承载比含水率下取得最大值。其余条件相同情况下，土体抵抗变形的能力主要受土体骨架影响，而土颗粒压实程度和土体初始含水率是影响土体骨架结构的两个重要因素。在低压实状态(85%)下，湿侧初始含水率(不低于击实最佳含水率)对土体骨架形成有不利影响；在较高压实状态(90%,94%)下，湿侧初始含水率(不低于击实最佳含水率)存在对土体骨架形成的最佳值。

路基中线处工后变形随深度的分布如图7(a)所示，路基顶面工后变形在横断面的分布形态如图7(b)所示。可见，在低压实度(85%)、高压实含水率(20.2%)条件下，虽然地基顶面的工后沉降较小，但路基自身的压缩变形显著增大，导致路基顶面的工后变形和不均匀变形明显大于其他工况；高压实含水率(20.2%)状态下的路基顶面不均匀变形普遍较大，而在最大承载比含水率状态下压实，压实度90%和94%条件下的工后不均匀变形基本相当。因此，从减小路基工后变形和不均匀变形的角度出发，对于天然含水率较高的花岗岩残积土，可以以最大承载比含水率为施工控制含水率，并可针对现场压实困难的情况，适当降低压实度控制标准。

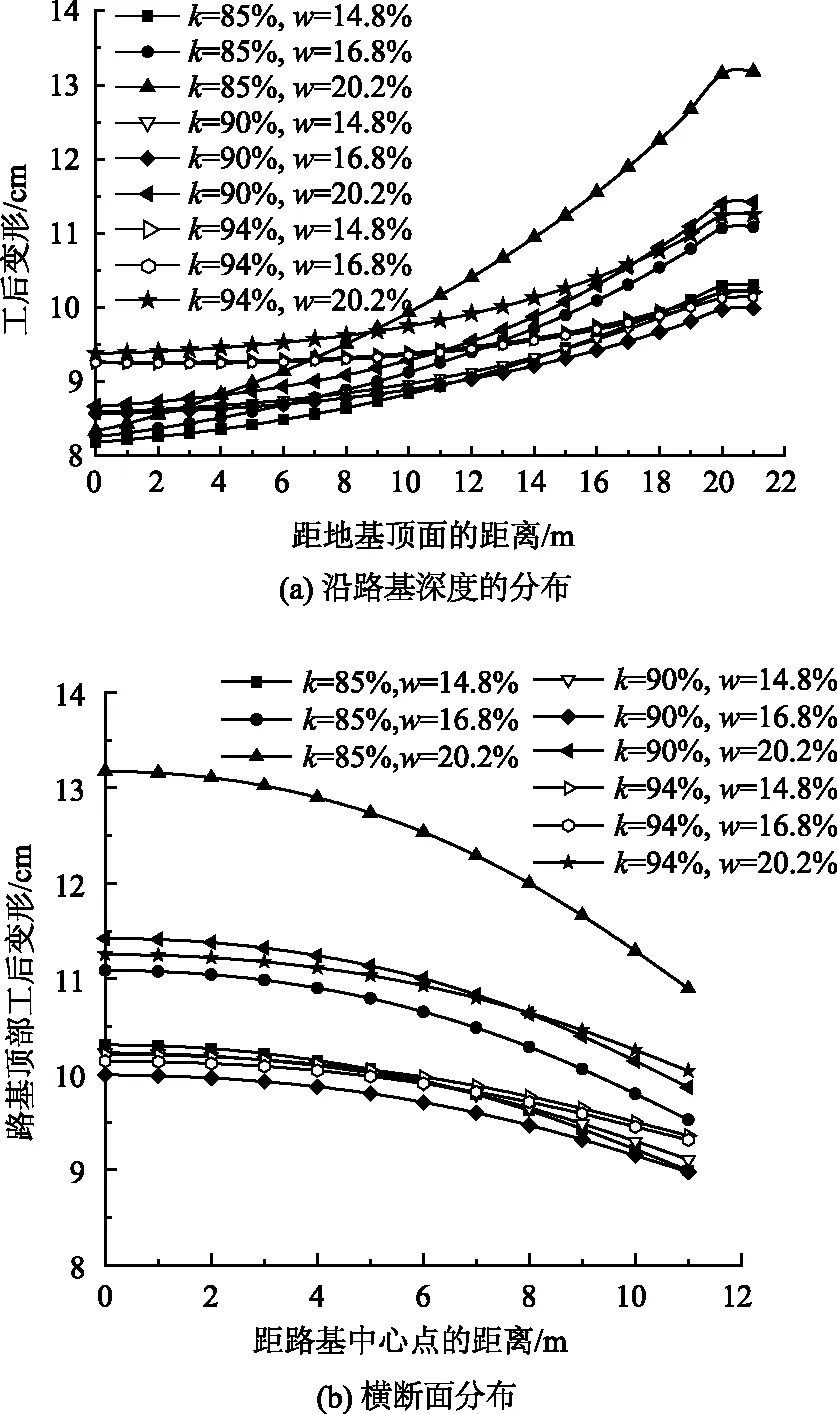
图7 不同压实状态下花岗岩残积土路基工后变形分布形态Fig.7 Distributions of post construction deformation of granite residual soil subgrade in different compaction states

3.2 填筑高度的影响

填料压实度为90%，初始含水率为20.2%，施工工序为速率0.5 m/d的分阶段填筑。对不同填筑高度下路基的工后变形(路面铺筑完成后1 080 d)进行分析，路基中线处工后变形随深度的分布如图8(a)所示，路基顶面工后变形在横断面的分布形态如图8(b)所示，工后的路基总变形、路堤压缩变形与填筑高度的关系如图9所示。可以看出，工后的路基总变形和路堤压缩变形均与填筑高度呈抛物线关系，随填筑高度的增加，路基工后变形迅速增大，差异变形量也逐步增大。由于路基工后变形包括地基工后变形和路堤压缩变形，地基变形在路基总变形中占据了很大的比重。如表3所示，在不同填筑高度下，地基的工后变形占路基工后总变形的70%以上。

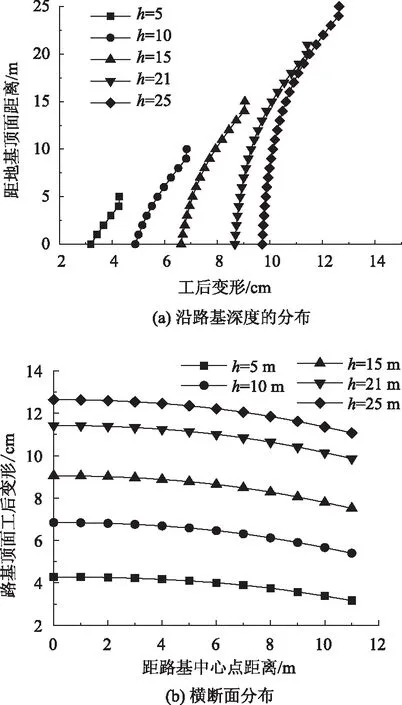
图8 不同填筑高度下花岗岩残积土路基工后变形分布形态Fig.8 Distributions of post construction deformation of granite residual soil subgrade at different filling heights

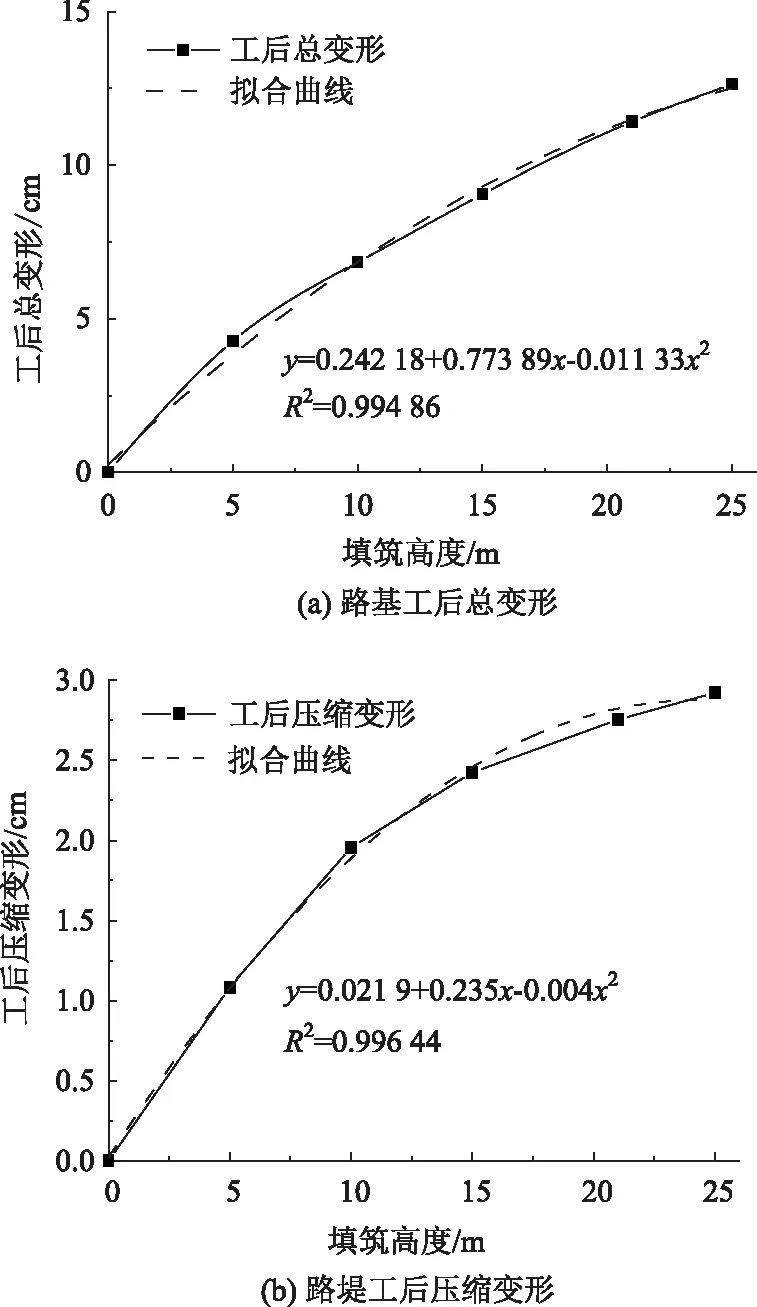
图9 填筑高度与路基工后变形的关系曲线Fig.9 Curves of filling height vs. post construction deformation of subgrade

表3 不同填筑高度下地基工后变形
Tab.3 Post construction deformation of foundation atdifferent filling heights

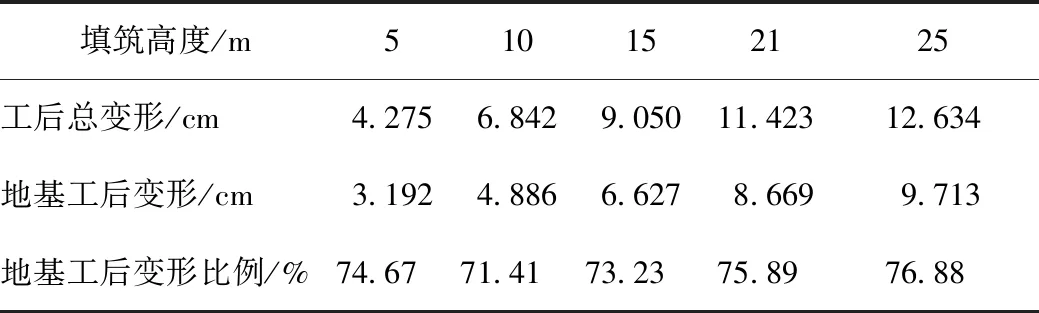
填筑高度/m510152125工后总变形/cm4.2756.8429.05011.42312.634地基工后变形/cm3.1924.8866.6278.6699.713地基工后变形比例/%74.6771.4173.2375.8976.88

3.3 施工工序的影响

对高度为21 m、填料压实度为90%和初始含水率为20.2%的花岗岩残积土路基采用不同的施工工序进行填筑。以路基顶面中心点作为特征点，分析路基沉降稳定阶段(A)、路面铺筑阶段(B)和工后固结阶段(C)的路基工后变形，如表4所示。

可知，对于不同施工工序下的花岗岩残积土路基而言，在路面铺筑阶段的路基工后变形量最大，并且随着填筑速率的增加，因路面铺筑所产生的变形量增大，但所占的比例逐渐降低。路面铺筑后路基自固结1 080 d，对于一次性填筑的路基，工后固结变形占路基工后总变形的比例约为59.39%，采用分阶段填筑的相应占比约为35%，且随着填筑速率的增加，工后固结变形所占的比例增大。这说明对于非饱和土路基而言，路基填筑速率过快，施工期固结沉降时间短，使得路基没有完全固结，因此部分变形在工后完成，工后变形及不均匀变形也相应增大。因此，在填筑路基时应当采用分阶段填筑，合理控制路基填筑速率。