粗粒盐渍土路基水热盐力耦合方程修正及试验验证

张莎莎，叶素纤，张 林,2， 杨晓华， 陈伟志

(1. 长安大学 公路学院，陕西 西安 710064；2. 山东省交通规划设计院， 山东 济南 250031； 3. 中国中铁二院工程集团有限责任公司，四川 成都 610031)

0 引言

在蒸发、降水、冻融循环等环境因素的长期影响下，盐渍土路基会产生盐胀、溶(融)陷等典型病害。盐胀、溶(融)陷与土中水盐迁移及其相变密切相关[1]。为研究盐渍土路基的水盐迁移及相变机理，国内外学者对盐渍土的盐胀影响因素[2-3]、盐(冻)胀机理及多场耦合理论[4-18]等展开了研究。

盐渍土路基的水盐迁移及相变是一个非常复杂的水-热-盐-力4场耦合问题，由于盐渍土的盐(冻)胀机理及本构模型研究进展缓慢，所以盐渍土的水-热-盐-力4场耦合理论研究有待完善。在20世纪50年代，Taylor等提出土壤溶质运移是分子扩散、机械弥散和化学反应的耦合过程。20世纪80年代,张效先指出，如果不考虑土体中的溶质和多孔介质的物理化学反应及土体中溶质自身的物理化学变化，则溶质的运移规律可用水的动力弥散方程表示[10]。目前，国内外进行了不少关于水、热、盐、力耦合的研究。黄兴法[5]在土壤物理基本定律的基础上，建立了(未)结冻、(非)饱和土壤的水热盐耦合运动通用模型；高江平等[6-9]在前人研究的基础上，建立了硫酸盐渍土水热盐力耦合数值模型；周发超[15]研究了饱和-非饱和土壤区域中的土壤水分及其中含有可溶性盐分等溶质的运动状况和积累变化；文献[16-17]采用现场试验、有限元数值模拟对硫酸盐渍土路基的温度场和水盐迁移规律进行了深入研究，并基于水动力学模型和质量守恒定律，在水分场方程和盐分场方程中分别引入修正等效含水量和等效含盐量的概念，以此为耦合因子建立水-盐-热耦合模型；王冬勇[18]以多孔介质中的溶质输运理论、水流理论和热传导理论为基础，建立了盐结晶、盐输运和水流耦合的控制微分方程。上述数值模型没有考虑溶质化学变化(水盐相变)对水分场和温度场的影响。但是，硫酸钠在降温过程中会发生化学变化生成芒硝，所以盐渍土路基盐分迁移规律不能简单地用水的动力弥散方程表示。同时，大部分数值模拟对象为室内盐渍土冻融试验，未研究多次冻融循环下盐渍土路基隔断层设置对水盐迁移的影响规律。

田亚护[11]指出水冰相变放热和芒硝结晶析出放热对温度场有较大影响；徐学祖提出水盐的迁移和相变会对土体的某些热力学参数产生作用。文献[12-18]提出水冰相变和芒硝结晶析出会造成土中液态水含量的降低。盐渍土的冻结温度一般低于非盐渍土的冻结温度，在低于冻结温度时，盐渍土中的液态水含量与含盐量、温度呈函数关系，冻结区中液态水的扩散率因固态冰阻滞作用而降低[19]。根据目前的研究现状，水盐迁移机理研究仅针对细粒盐渍土开展，对于我国西北地区、西亚及中亚等地分布较广泛的粗颗粒盐渍土而言，还缺乏相关研究内容。同时，粗粒盐渍土盐(冻)机理亦有待完善。

为建立更符合实际的粗颗粒盐渍土路基水-热-盐-力4场耦合数值模型，明确隔断层设置对粗颗粒盐渍土路基水盐迁移的影响规律，在前人研究的基础上，本研究考虑水盐相变对水、热、盐、力4场的影响，同时为满足粗颗粒盐渍土的工程特性，修正了目前已建立的水、热、盐微分方程。以非饱和土的渗流及热传导理论为基础，引入水、盐各相含量和土体温度之间的经验关系式作为联系方程，建立粗粒盐渍土路基的水-热-盐-力耦合微分方程组。同时，采用COMSOL软件的二次开发模块，实现粗粒盐渍土路基4场的全耦合数值模拟，再与砾类盐渍土室内大型冻融循环试验结果做对比，验证所建立的水-热-盐-力4场耦合模型的有效性，最后通过试验结果和前人研究成果对建立的粗颗粒硫酸盐渍土路基方程进行进一步的讨论和修正。

1 盐渍土水-热-盐-力耦合微分方程

1.1 温度场控制微分方程

对于二维的水-热-盐耦合问题，本研究基于傅里叶定律，考虑芒硝结晶相变的放热影响，将水冰相变和芒硝结晶相变的潜热作为热源处理，盐渍土热传导微分方程可修正为：

(1)

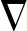
1.2 水分场控制微分方程

在负温下，由于盐渍土中一直存在液态水[13]，其迁移过程遵循达西定律。据Richard方程，同时考虑产生的孔隙冰对液态水迁移通道的阻滞[19]和水冰相变及芒硝结晶相变降低土中液态水含量的作用，非饱和盐渍土路基中的液态水迁移微分方程可修正为：

(2)

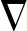
其中，盐渍土含水率由冰、液态水、芒硝结晶水3部分构成。考虑到冰、芒硝和水的密度不同，土的体积含水率定义为:

(3)

式中,θu为土中液态水的体积含量;ρI为冰的密度；ρw为水的密度。

1.3 盐分场控制微分方程

根据已有研究，如果不考虑将土体中的溶质和多孔介质的物理化学反应及溶质自身的物理化学变化，则溶质运移规律可用水的动力弥散方程表示。所以在一般情况下，溶质和水溶剂的浓度梯度方向相反，扩散方向也相反[10]。但是降温导致硫酸钠结晶生成芒硝，不仅降低了液态水的含量，同时降低了溶质的浓度，导致二者的扩散迁移方向相同。所以，盐分迁移控制方程应修正为：

(4)

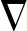
盐溶液浓度c的确定及表达：在土中盐溶液非饱和状态下，盐溶液的浓度受含盐量影响；在土中盐溶液饱和状态下，盐溶液的浓度受温度(溶解度)影响。所以，在COMSOL软件中如何准确表达盐溶液的浓度对建立盐分控制方程十分关键。

盐溶液浓度表示为：

(5)

式中，ss为在COMSOL软件中的书写形式；ssJ=[ss-rongjiedu(T)θu]×[ss>rongjiedu(T)θu]，是在COMSOL软件中的书写形式,rongjiedu(T)为硫酸钠溶解度拟合函数,ss>rongjiedu(T)θu是一个条件函数，表示溶液处于过饱和状态。所以，当溶液处于非饱和状态时，COMSOL默认ssJ=0，c=ss/θu受含盐量的控制。当盐溶液处于过饱和状态，c=rongjiedu(T)仅受温度影响。

1.4 联系方程：水冰相变和芒硝结晶过程

式(1)、式(2)、式(4)中存在5个未知变量：土体温度T、芒硝含量θc、冰含量θi、液态水含量θu、含盐率mss。所以，仍需要建立2个联系方程才能计算出5个未知变量。

根据前人研究结果做出如下假定：(1)冻结温度以上只发生盐胀；(2)冻结温度以下发生冻胀；(3)冻结温度以下不考虑盐胀作用；(4)不考虑温度对土体热胀冷缩的影响。

1.4.1冻结温度以下冰的体积含量与未相变水体积含量的经验关系

徐学祖[19]根据试验数据得到了冻土中未冻结含水率的经验关系公式：

(6)

式中，ω0为土体的初始含水率；ωu为某个温度下土体未冻水含量；T为土体温度;Tf为土体冻结温度；B为常数，可按砂土为0.61，粉土为0.47，黏土为0.56取经验值[19]。

同时，因建立理论模型，引入“冰水比”的概念，表示冻结过程中盐渍土孔隙中的冰体积含量与未相变的水体积含量之比，记为BI，表示为：

(7)

式中,θI为孔隙冰体积含量；θu为液态水含量；T为土体温度;Tf为土体冻结温度；B为常数。

1.4.2冻结温度以上未相变水含量与芒硝结晶量的关系

假定：当盐渍土中的硫酸钠溶液达到过饱和状态时，环境温度的降低会导致盐渍土中的孔隙盐溶液中部分硫酸钠吸水结晶(芒硝晶体)，孔隙盐溶液浓度降低，孔隙中的液态水减少。

根据上述假定，得到的芒硝结晶在COMSOL软件中的理论表达式：

[ss>rongjiedu(T)θu]，

(8)

式中,ρmx为芒硝密度；ρs为土粒密度。

据已有研究，在32.4 ℃时，硫酸钠的溶解度最大；当低于32.4 ℃时，硫酸钠的溶解度随环境温度的降低而迅速下降，且其受氯化钠的浓度影响显著。根据已有试验数据，发现不同温度下硫酸钠溶解度与氯化钠浓度之间存在良好的二次函数关系，即[20]：

rongjiedu(T)=(Ac2+Bc+M)/100，

(9)

1.5 应力场控制方程

根据上文假定，盐渍土体积膨胀主要由冻结温度以上的盐胀体积膨胀和冻结温度以下的冻胀体积膨胀组成，在本研究数值模拟计算中取冻结温度为0 ℃。

冻胀和盐胀的相变方程分别为水冰相变和芒硝结晶相变。

水冰相变：H2O(液态)→H2O(冰)

假定单个土孔隙为球形，半径为r，土孔隙含水率为ω，水的体积为Vω。液态水全部冻结，则水体积的变量ΔVω为：

(10)

芒硝结晶相变：

Na2SO4+10H2O=Na2SO4·10H2O

芒硝结晶相变根据硫酸钠的状态分为两种情况：(1)硫酸钠全部溶于液态水时，体积增大约0.23倍；(2)硫酸钠为固体时，体积增大约3.18倍(其中水为外来水)。本研究所模拟的盐渍土路基含盐量较低，硫酸钠全部溶于液态水中，芒硝结晶相变采取第1种相变方式。

冰的含量和芒硝结晶水的含量都可借助上文控制方程求得。水冰相变和芒硝结晶相变引起的土体积应变εv表示为：

εv=0.09θI+0.23swJ，

(11)

式中,θI为孔隙冰体积含量；s为位移；wJ为芒硝结晶含水率。

假定土体为各向同性，土的盐(冻)胀变形在各个方向上是相等的，即：

(12)

γxyv=γyzv=γzxv=0，

(13)

式中，εxv，εyv，εzv为膨胀引起的正应变分量。γxyv，γyzv，γzxv为膨胀引起的剪应变分量。

2 基于COMSOL二次开发的水-热-盐-力耦合数值模型

由于COMSOL Multi-physics有限元软件可以求解非线性微分方程组，利用其中的PDE模块进行二次开发，建立粗粒盐渍土的水-热-盐-力耦合数值模型。

软件中的偏微分方程和边界条件函数表达形式为：

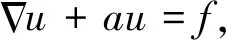
(14)

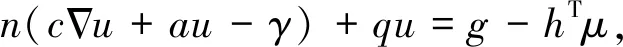
(15)

u=γ, 在Γ之上,

(16)

式中，ea为质量系数；u为拉格朗日方程表示的位移；da为阻滞系数；μ为拉格朗日乘子；g为边界上的源项；α为保守通量对流系数；γ为保守通量源项；β为对流系数；a为吸收系数；f为源项；c为扩散系数；h,γ为方程系数；q为边界上的吸收系数；Ω为计算区域；Γ为计算区域的边界；n为边界Γ的外法线方向；式(6)为求解域上的方程；式(7)为Neumann边界条件；式(8)为Dirichlet边界条件。

将水-热-盐耦合控制微分方程组转换成软件识别的方式，而应力场方程采用COMSOL的相变膨胀模块。

温度场控制方程：

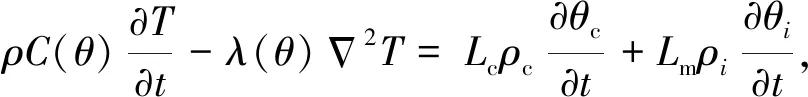
(17)

式中Lm为冰水相变潜热。

水分场控制方程：

kg(θu)]=0。

(18)

盐分场控制方程：

(19)

在非饱和土的渗流分析中，采用Van Genuchten(VG)滞水模型和Gardner渗透系数模型；同时，将相对饱和度S定义为：

(20)

式中，θr为土的残余含水率；θs为土的饱和含水率。

3 粗粒硫酸盐渍土路基水-热-盐-力耦合数值模型验证

3.1 试验方案及数值模型基本工程参数

为验证所提水-热-盐-力耦合数值模型的有效性，采用砾砂(试样参数见表1)开展冻融循环试验。试样在室温下闷料24 h，然后将其按93%压实度分层击实到高160 cm、内径30 cm的有机玻璃试筒内，最终土柱高150 cm。因为随着环境温度的降低，低温在土柱中的传递呈梯度分布特征，且根据以往研究经验，低温影响范围有限，所以温度监测点位(设置高度)为145，135，125，115，105，95，80，65，50，35，20 cm。有机玻璃筒周围包有一层厚保温材料，以隔断试样与周围环境的热量交换。在顶端制冷板上安置百分表来监测土样的变形量。顶端制冷板作为上覆荷载，约为0.7 kPa。同时，有机玻璃试筒下端连接盛有饱和盐水的马氏瓶，以模拟地下水的补给。室内开放系统下大型冻融循环试验装置的简化示意图见图1。

表1 砾砂级配表Tab.1 Gradation of gravel sand

表2 冻融循环试验中的土体性质及其边界条件Tab.2 Soil property and boundary condition in freeze-thaw cycle test

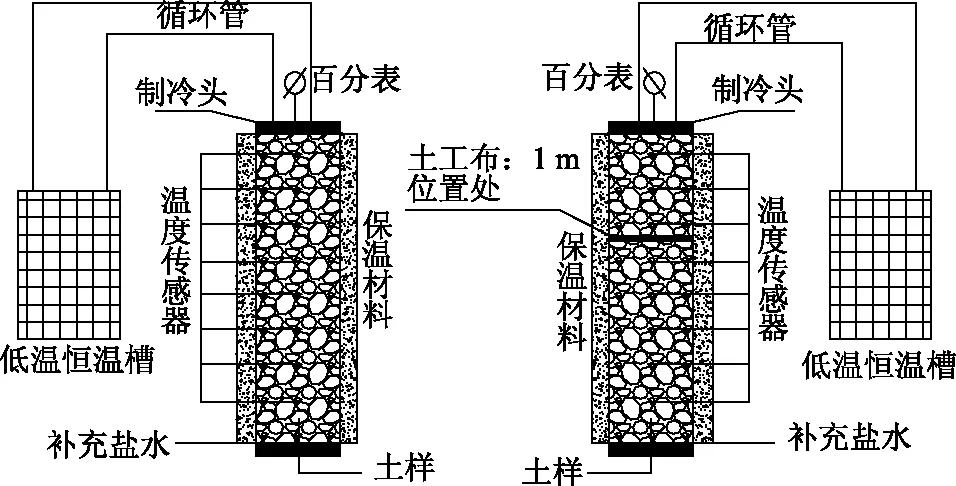
图1 大型冻融循环试验装置示意图Fig.1 Schematic diagram of large-scale freeze-thaw cycle test equipment

根据已知的砾类土毛细水上升高度的研究成果，试验分为两组，一组土样内部不设置土工布，另一组在土样高100 cm处设置1层可阻碍水盐迁移的土工布来对比观察土工布对盐胀和水盐迁移的影响。利用低温恒温槽和附有保温膜的大型有机玻璃试筒对土样进行单向降温和自然升温试验，以模拟冬季降温过程和来年春季升温过程。单向降温条件及试验边界条件见表2，其中，最低环境温度设置为-20 ℃，数模参数见表3，共7个冻融周期。试验结束后，在土柱相应位置处取土样进行含水率和含盐量试验。

表3 数值模型参数Tab.3 Numerical model parameters

鉴于COMSOL为基于有限元原理，需要在冻结锋面处建立一个过渡函数Heavide(T)对数值模型参数做连续性处理。

C=Cf+(Cu-Cf)×Heavide(T)，

(21)

m=mf+(mu-mf)×Heavide(T)，

(22)

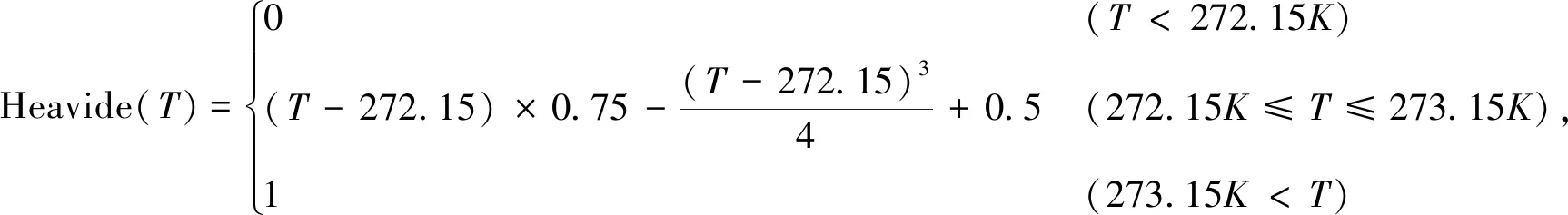
(23)

式中，C为土体热容；Cf为冻土热容；Cu为融土热容；m为土体导热系数；mf为冻土导热系数；mu为融土导热系数。

同时，在数值计算过程中，对土工布的设置和处理时，考虑了毛细作用对水盐迁移起绝对影响的作用。本研究将毛细作用按水分的自由扩散处理。土工布的作用在于完全隔断水盐迁移，故在模型中将土工布做封闭的边界处理。

3.2 数值计算结果与试验结果对比分析

将冻融循环后的试验结果和数值模拟结果进行对比，其结果见图2～图3。试验过程中的土温、氯离子和硫酸根离子含量的变化情况分别见图4、图5。

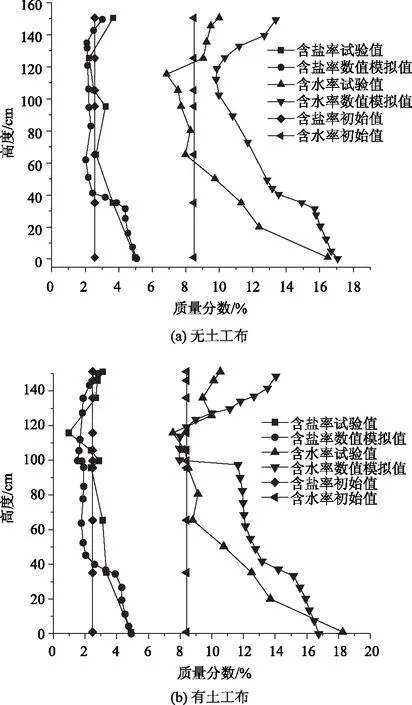
图2 七次冻融循环后水盐分布规律Fig.2 Water and salt distribution after 7 freeze-thaw cycles

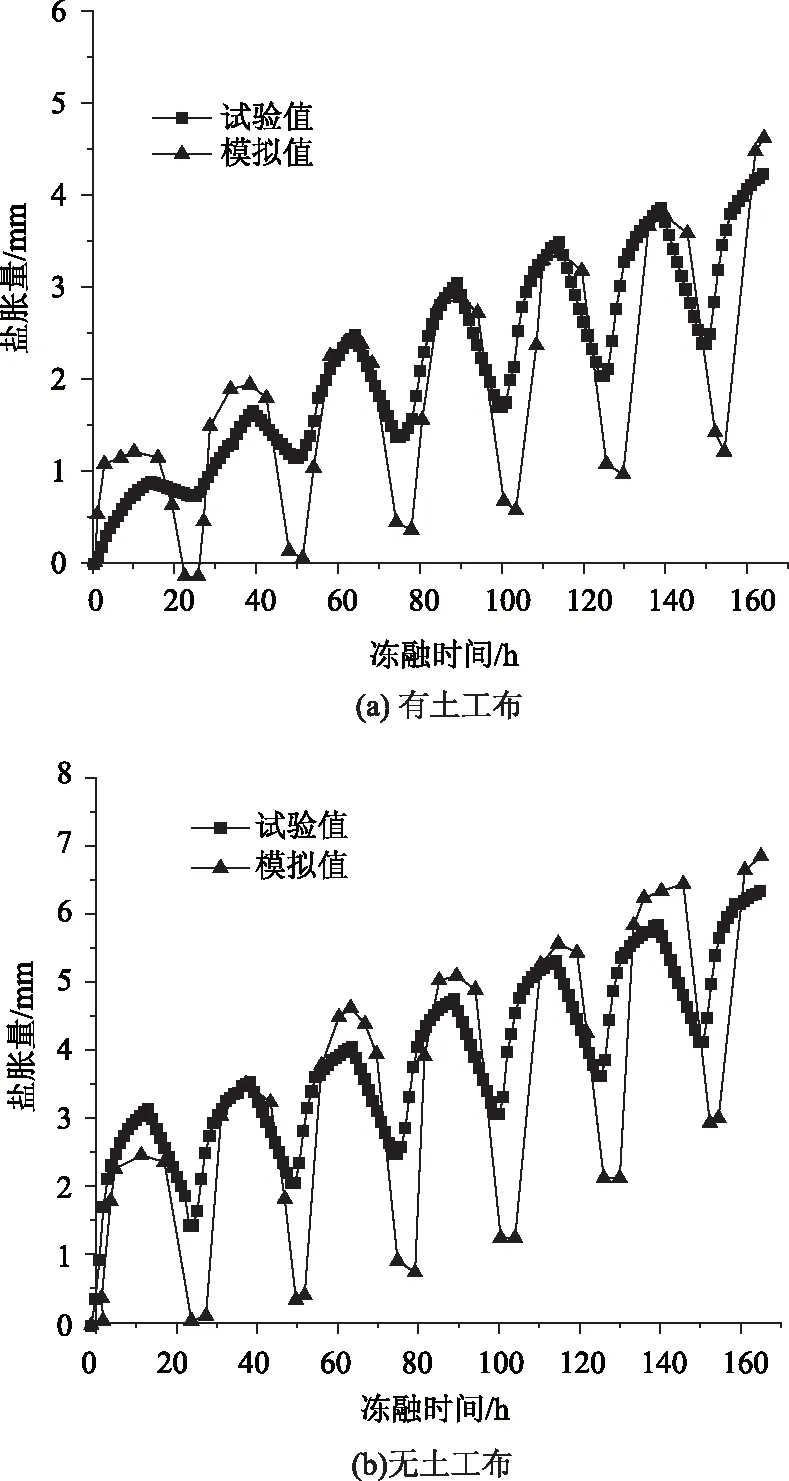
图3 盐胀量随冻融循环次数变化曲线Fig.3 Curves of salt expansion amount varying with freeze-thaw cycles

从图2～图3可知，数值模拟结果与试验结果基本吻合，说明建立的数值模型是有效的。

图4 土体各层温度变化曲线Fig.4 Temperature changes of different soil layers注：105 cm以下土层温度变化很小，基本稳定在20 ℃附近，并没有在曲线中展示，且土工布对温度传递无影响。

图5 七次冻融循环后离子分布曲线Fig.5 Curves of ion distribution after 7 freeze-thaw cycles

由温度监测结果(图4)可知，在7次冻融循环试验中主要受低温作用影响的区域为高度105～150 cm(从土柱底端算起)，即制冷端下方0～45 cm为该工况下的低温影响敏感区段。在低温影响敏感区段内，水盐均向冷端发生迁移且迁移程度不可忽视，试验结果中表层含水率从初始8.5%增加到10%(无土工布)和10.6%(有土工布)。表层含盐量从初始2.6%增加到3.69%(无土工布)和3.24%(有土工布)。之所以无土工布的土体表层含水率反而稍小，是因为土工布设置的位置为该工况土体的毛细水强烈上升高度影响范围之上，在无土工布的工况中，土体中的水受到重力向下迁移的作用强度大于毛细水上升的作用强度，导致无土工布土体受低温影响迁移上升的水量相对减小。而盐分的滞留作用相对水分更显著，所以表现出的迁移特征不一致[21]。受低温影响，在扩散作用和土体基质吸力的作用下，未降温区域的盐分和水分分别向降温区域迁移，土样中间部位的水盐含量均低于初始含量。在低温影响敏感区段内，温度是水盐迁移的主导驱动力。

土柱下半部位，即温度相对稳定区段，由于试验模拟的是有外来水源补给的工况，该区段温度作用相对弱化，毛细作用较显著，该砾砂细粒组含量高达50%，其毛细水强烈上升高度约70～90 cm。在毛细水强烈上升高度区间，水盐的迁移量远大于受低温影响区域的迁移量，说明在毛细水上升区间，毛细作用对水盐迁移的影响最主要。

由于本工况中土工布的位置高于毛细水强烈上升高度，土工布对毛细水的阻断作用并不明显。但是土工布依然阻碍了水盐迁移路径，高度115 cm处的有土工布的土柱含盐量因为不能得到下方水盐补充，其小于无土工布相应位置的含盐量，从而抑制了土工布以上填土的次生盐渍化和盐胀程度。但是土工布下方出现了一定程度的盐分富集现象。

由图3～图5可知，两个土样在冻融循环中都出现了盐胀量累积，且没有发生“体缩”，累积最大盐胀量分别为6.29 mm(无土工布)和4.24 mm(有土工布)，土工布的设置可减少盐胀量约32.6%。每个冻融循环周期，有土工布的土样盐胀量和融陷量相对较小。土工布在一定程度上起到了抑制路基土体盐胀、融陷变形的效果，其对第1周期的盐胀量抑制效果最显著。

土工布隔断水盐迁移路径后，盐胀累积性明显减弱。盐渍土盐胀的累积性主要原因是水盐向表层迁移和土体结构受盐胀力破坏后的难恢复性。所以，土工布隔断水盐迁移路径，抑制了水盐向表层迁移的程度，阻碍了部分水盐进入低温影响敏感区段，抑制了盐渍土的盐胀。

在低温影响敏感区段，氯离子与硫酸根离子均向土样表层(冷端)迁移，此类硫酸盐渍土的硫酸根离子迁移幅度相对较大。在温度变化幅度较小区域，土工布下硫酸根离子的富集程度较强。

3.3 讨论

盐渍土土样在降温过程中会出现盐(冻)胀现象。冻结温度以上，盐渍土发生盐胀。冻结温度以下，盐渍土主要发生冻胀。降温过程中，土中的水和硫酸钠会发生相变。硫酸钠结晶相变和水冰相变是造成盐渍土盐冻胀的直接因素。以下讨论与盐渍土盐冻胀机理密切相关的盐渍土中未相变水和结晶盐含量变化规律。

盐渍土含水率组成：假定建立的盐渍土路基计算模型中的孔隙均为球形，且不同半径的孔隙在盐渍土中是随机分布的，根据水在其中的存在形式，可将水分为4部分：结晶水、固态水、自由未冻水、非自由未冻水。盐分的存在形式可分为3部分：结晶盐、自由盐溶液、非自由盐溶液。

土孔隙半径对芒硝晶体和冰晶形成的影响：鉴于孔隙大小对晶体生长的影响和晶体均匀成核，土壤中的盐晶可以看作球体。基于结晶理论，总过剩自由能等于表面过剩自由能ΔGs加上体积过剩自由能ΔGv。ΔGs为正，与2r成正比(r为球半径)；在过饱和溶液中，ΔGv是负的，与r3成正比。所以有：

(24)

式中ΔG为总过剩自由能。

(25)

(26)

对于单种溶质而言，ΔGv的变化可以由化学势的变化来表示：

(27)

式中，μ为化学势；Vm为盐晶体的摩尔体积；R为理想气体常数；Ua为过饱和比。

(28)

因此可得芒硝结晶的临界半径范围为2～8.5 nm (20～-15 ℃)[22]。

在水冰相变过程中，忽略水冰的密度差，在冰液界面上的Gibbs-Duhem相平衡关系[23]为：

(29)

式中，ΔP水冰界面压力差；Pi为冰水界面上的冰压力；Pw为冰水界面上的水压力；Γ为水冰相变潜热；ΔT=Tm-Tf，Tm为常压下自由体积水的冻结温度，Tf为冻结温度。

同时，水冰界面上的压力差可由Young-Laplace方程表示：

ΔP=Pi-Pw=γiwκ，

(30)

式中，γiw为水冰界面自由能；κ为水冰界面曲率，曲率越大，表示曲线弯曲的程度越大。

结合式(29)和式(30)，可得到常压下自由体积水的冻结温度与冻结温度之差ΔT的Gibbs-Thomson公式为：

(31)

做进一步推导：

(32)

对于多孔介质而言，半径为γfp的球形孔隙，曲率为κ=2/γfp。然后将κ=2/γfp代入式(21)，则该孔隙对应的冻结温度为：

(33)

式(33)表明，当冻结温度达到Tfp时，只有半径大于rfp时,孔隙中的水会产生冻结，其余较小孔隙中的水则会保持液态。因此，对于多孔材料而言，在低温情况下，随温度的降低，内部水的冻结是从大孔隙向小孔隙发展。

当冻结温度为Tf时，冰晶形成的临界半径rf为：

(34)

可以得到rf=50 nm。

WAN等[22]研究表明，盐溶液的浓度决定了冻胀、盐胀发生的先后顺序。所以本研究依据已有研究做出如下假定：(1)盐水质量比小于1.3∶18的土样，其未相变水的变化只受冰水相变的影响，不受芒硝结晶相变的影响；(2)盐水质量比不小于1.3∶18 的土样，其未相变水的变化先受芒硝结晶相变影响，然后在冻结温度以下只受冰水相变影响。

盐结晶质量随过饱和比的变化：盐结晶在多孔介质材料内发生的初始条件是盐溶液的过饱和比大于盐结晶的初始过饱和比。一旦结晶发生后，只要溶液处于过饱和状态，结晶就不会停止直到溶液处于饱和平衡状态。

盐结晶与温度和过饱和比的关系为：

(35)

式中，ms为结晶盐的质量；Kcrystal为随温度降低而降低的参数；U0为初始过饱和比率；n为孔隙率。

由于芒硝结晶的临界半径范围为2～8.5 nm(20～-15 ℃)，且冰晶形成的临界半径rf=50 nm(计算参数取值：γiw=30 mN/m,Tf=-1 ℃)。同时，压实过后的盐渍土的土孔隙半径分布范围从几纳米到几毫米。根据经验估计，98%左右的土孔隙半径大于芒硝结晶的临界半径；大部分土孔隙半径大于50 nm。所以，几乎所有土孔隙不会对盐晶的形成造成影响，而冰晶的形成在0～-5 ℃之间几乎全部完成。由于盐结晶量比较小，且土为非饱和土，盐结晶对土孔隙的填充作用对冰晶的形成影响可以忽略不计。在冻结温度之上，如果没有发生芒硝结晶，则在降温冻结过程中可以忽略盐胀。

所以在不考虑结晶速率的情况下，结晶盐和未相变水与温度的关系[7]应修正为：

(36)

θu=θt-1.267 6ms，

(37)

式中，ms为结晶盐的质量；m为盐的总质量；ξ(T)为溶解度函数；Ua为过饱和比；w为水的总质量；θu为未相变水的质量；θt为t时刻的总水量。

4 结论

(1)基于非饱和土渗流和热传导理论，考虑水盐相变对4场的影响，分别对已建立的温度场、水分场、盐分场微分控制方程进行修正，建立了适用于粗粒盐渍土路基水-热-盐-力4场耦合微分方程组，并利用COMSOL Multi-physics软件建立了粗粒盐渍土路基4场全耦合数值模型，然后通过室内大型冻融循环试验对数值模拟结果的有效性进行了验证。

(2)在开放系统下的冻融循环工况中，砾砂类(细粒组含量50%)硫酸盐渍土的毛细水强烈上升高度约70～90 cm。在毛细作用和温度影响下，砾砂盐渍土路基中的水、盐均向冷端迁移，其会导致土工布下方出现盐分聚集现象，其中硫酸根离子富集程度较强。

(3)制冷端下方0～45 cm为该工况下的低温影响敏感区段，土工布设置应综合参考土类的毛细水上升高度和低温影响敏感区段。由于土工布阻隔了水盐向低温影响敏感区段迁移，达到了抑制盐胀的作用，盐胀量抑制程度可达到30%以上。

(4)降温导致水盐结晶相变，使土体膨胀；升温导致盐晶和冰晶融化，使土体融陷。为进一步研究粗粒盐渍土盐(冻)胀机理，可引入过饱和比解释盐渍土盐胀量与硫酸钠结晶之间的关系，建立粗粒盐渍土盐(冻)胀模型，建立符合实际的4场耦合方程。