剪切条件下单裂隙细观流动特性研究
2020-03-30李铭华
王 敏,李铭华
(1.长江勘测规划设计研究有限责任公司,湖北 武汉 430010;2.南京市长江河道管理处,江苏 南京 210011)
在大型水电和地热能源开发,石油、天然气、地下水开采及核废料深层埋置等工程问题中,均涉及裂隙岩体渗流及水力耦合机理的研究,岩石裂隙细观流动特性是上述机理研究的关键问题之一[1-4]。
岩体裂隙中的细观流动满足不可压缩流体动量守恒方程,即Navier-Stokes(N-S)方程:
(1)
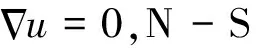
(2)
式中,Q为流体流量,e为平板裂隙开度,J为水力梯度。天然裂隙表面凹凸不平,裂隙结构之间的开度也并非定值,因此立方定律只适用于裂隙开度变化较缓或局部区域,公式(2)也被称为局部立方定律。
式(2)中的裂隙开度e为物理宽度,也称机械开度或力学开度,为考虑裂隙粗糙度的影响,常用等效水力开度eh代替裂隙机械开度,不同学者通过大量室内裂隙渗流试验提出了各自的机械开度与等效水力开度之间的换算公式[5-7]。为有效地建立机械开度与水力开度的关系,通常需要引入描述裂隙粗糙度参数,如裂隙粗糙度系数Jrc,为考虑裂隙剪切错动对裂隙等效水力开度的影响,Olsson等[8]通过实验研究提出了在剪切错动条件下,机械开度与水力开度的换算关系:
(3)
式中:ds为裂隙剪切位移,dsp为峰值剪应力时的剪切位移,Jrc 0为裂隙的初始粗糙度系数,Jrc mob为剪切错动后的粗糙度系数。
从式(3)中可以看出,剪切位移对裂隙等效水力开度影响较大,但式(3)未考虑裂隙流态的影响,且公式是根据实验数据拟合得到,未揭示剪切位移对裂隙渗流影响的机理。本文采用格子玻尔兹曼模型(Lattice Boltzmann Method,简称LBM)[9-10]模拟单裂隙细观渗流过程,研究在剪切条件下,考虑不同流速(不同雷诺数)对细观流动特性的影响,研究结果将为建立机械开度和等效水力开度的宏观规律提供基础。
1 数值模拟方法
1.1 MRT-LBM格子模型
在格子玻尔兹曼模型中,多松弛模型(Multiple-Relaxation-Time,简称MRT)由于采用多个因子控制LBM中的碰撞过程,能有效克服单松弛模型带来的数值稳定性差且存在渗透率与黏性相关等不足,并且能计算中等雷诺数条件下的流动过程[11]。在MRT-LBM格子模型中,速度分布函数f满足如下演化方程[12]:
fi(x+eiΔt,t+Δt)-fi(x,t)=-M-1SM[f(x,t)-
feq(x,t)]
(4)
fi(x+eiΔt,t+Δt)-fi(x,t)=-M-1S[m-meq]
(5)
式中:S为非负松弛参数矩阵,ei为i方向的权函数,m=Mf,M为空间转化矩阵,feq为平衡态速度分布函数。
1.2 方法验证
采用Fortran 90语言编写LBM计算程序[13],并采用圆柱绕流模型验证程序的有效性和正确性。圆柱绕流模型的进口采用速度边界,采用Zou等[14]格式实现,出口为充分发展边界,上下边壁及中间圆柱为速度无滑移边界,采用非平衡外推格式[10-11]。取雷诺数为10、20和40三个计算工况。
雷诺数Re为40时的流速分布如图1所示,由图可见,流速在x方向和y方向均具有较好的对称性,且在圆柱边壁流速为零,上述结果表明计算方法在曲面边界处理方面具有良好的计算稳定性。
圆柱绕流模型在不同雷诺数条件下的流线如图2所示。由图2可见,圆柱后方均出现稳定的涡流,且漩涡面积随着雷诺数的增大而增大。为验证本文计算程序的正确性,采用涡流的相对长度2Leddy/D和分离角度θs两个无量纲参数定量描述涡流区域的几何特性,其中Leddy为涡流区域最远点到圆柱的距离,并与Ding等[15]的计算结果进行对比,对比结果如表1所示,在不同雷诺数条件下,本文的圆柱绕流模拟结果与前人的模拟结果基本一致,表明本文模拟方法及计算程序的正确性成立。
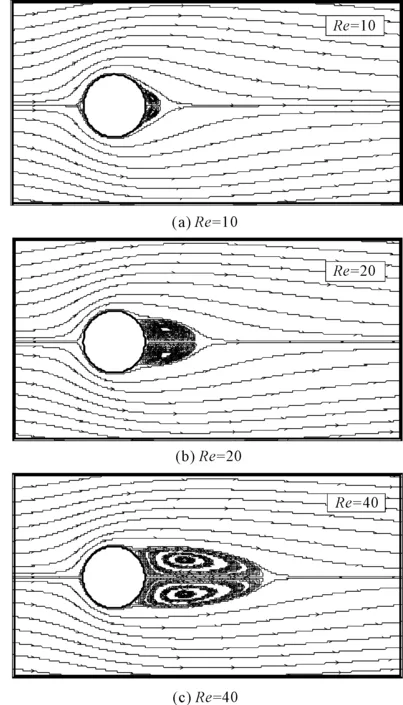
图2 不同雷诺数条件下的流线图
2 剪切条件下单裂隙流动特性分析
2.1 物理模型
为获取真实裂隙结构面模型,首先采用巴西劈裂法[16]对岩体试样进行人工劈裂,得到粗糙裂隙面,再利用三维非接触式轮廓仪扫描裂隙面,由采集的裂隙面数据生成的三维形貌如图3所示,裂隙面数据密度为0.2 mm,Z方向的数据精度为10 μm。
如图3所示,选取扫描裂隙面上的轮廓线A-A′为作为二维裂隙模型的下轮廓线,并将A-A′轮廓线竖直平移1 mm形成上轮廓线,得到二维裂隙模型,记为Model 0,如图4所示。将上轮廓线向水平方向分别平移1.0 mm、2.0 mm、3.0 mm和4.0 mm,可得到剪切位移ds分别为1.0 mm、2.0 mm、3.0 mm和4.0 mm条件下的二维裂隙几何模型,分别记为Model 1—Model 4。对裂隙模型Model 0—Model 4的力学开度进行统计分析,结果如表2所示,对于完全吻合的裂隙模型Model 0,裂隙上下两条轮廓线的相关系数为1.0,随着剪切位移的增加,吻合程度降低,相关系数逐渐减小,裂隙开度的均方差也逐渐增大,说明裂隙开度的变异性随剪切位移的增大而逐渐增大。
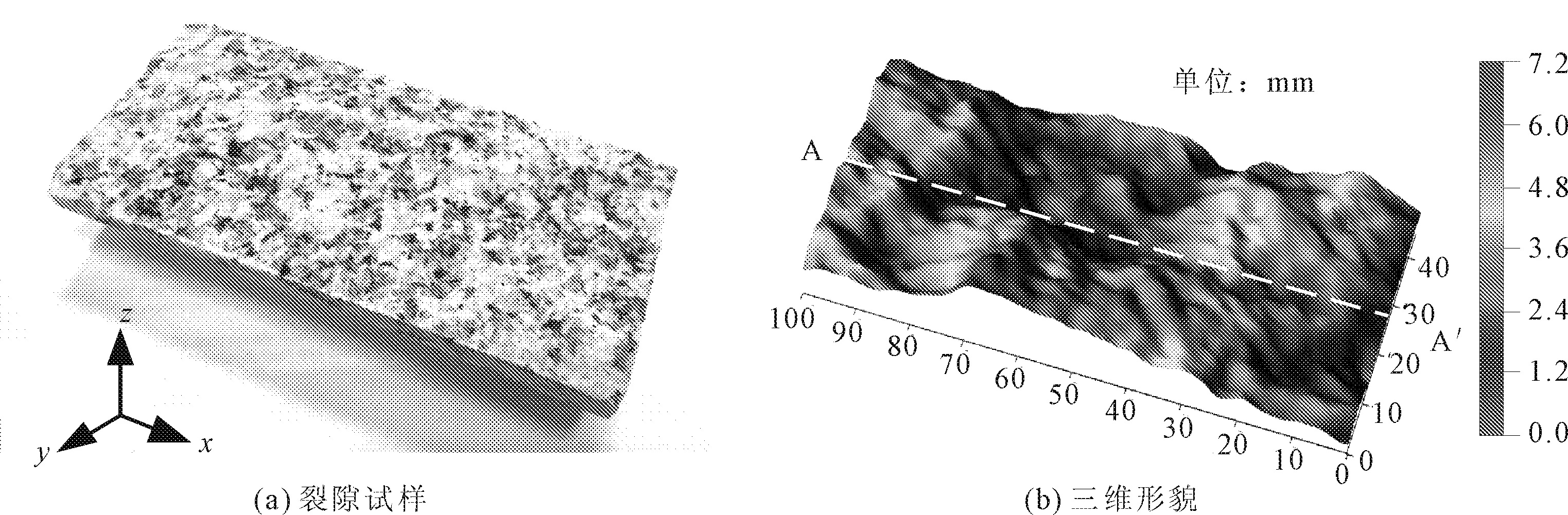
图3 裂隙试样的三维形貌
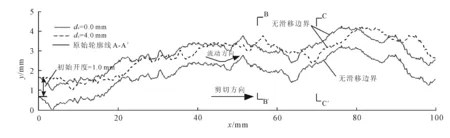
图4 单裂隙几何模型
2.2 模拟条件

表2 裂隙模型力学开度统计
2.3 流速分布
各裂隙模型B-B′截面(位置见图4)处流速随剪切位移的演化如图5所示,图5分别给出了雷诺数为1和100两个计算工况下的结果。从图5中可以看出,在不同雷诺数条件下,B-B′截面均存在一定大小的y方向流速uy,且速度大小受开度变化的影响,可能存在正负两个方向的uy速度;当Re=1时,即低雷诺数条件下,流速ux分布为典型的抛物线分布,且不同剪切位移ds条件下的ux速度分布形式基本一致,x方向的流速的最大值与截面处的裂隙开度成反比;当Re=100时,即高雷诺数条件下,ux流速在靠近裂隙边壁处的低流速区域有所增加,同时在剪切位移ds=4.0 mm的条件下,ux速度在一定宽度范围内出现负方向的流速,说明裂隙内出现明显的回流现象。
为揭示在高雷诺数条件下裂隙的细观流动特征,图6给出了不同剪切位移条件下的流线图。从图6中可见,当ds=0 mm时,裂隙内流线与流动主通道基本平行,随着剪切位移值ds逐渐增加,在裂隙内逐渐出现了大小不一的涡流,主要出现在开度变化剧烈的区域,且涡流数量随着剪切位移的增加而增加,涡流大小也逐渐增大。当ds=4.0 mm时,裂隙内的涡流增加较为明显,局部区域的涡流逐渐占据裂隙渗流的主通道,说明在高雷诺数条件下,剪切位移带来的裂隙开度变化极大地影响裂隙通道内的流动状态。
2.4 涡流的形成和演化
图7给出裂隙模型Model 4(ds=4.0 mm)在不同雷诺数条件下局部区域内(x=50 mm~60 mm)的流线图。由图7中可见,当雷诺数较小时(Re=1),裂隙内无涡流产生,随着雷诺数增大,涡流才开始出现;当Re=50~100,涡流的数量开始增多,涡流的面积也逐渐增大,导致裂隙内的有效过流区域减小;当Re=100~150,涡流面积在增大的同时,一些较大的涡流会在裂隙边壁分裂出较小的次生涡流,原来一些较小的涡流会逐渐合并形成范围更大的涡流,说明此时裂隙内的形成了较强的紊流流态。
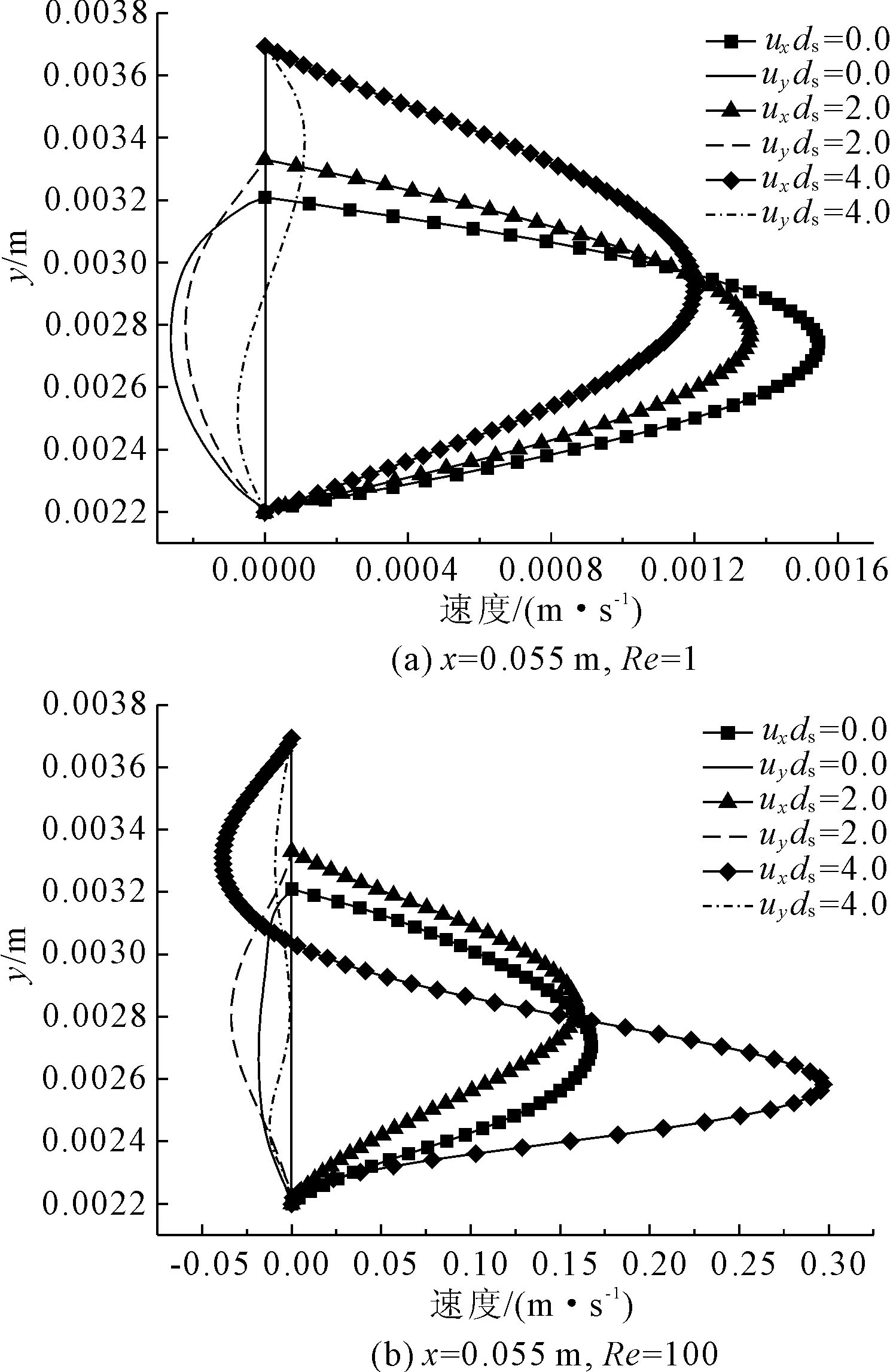
图5 速度随剪切位移的演化图(B-B′:x=55 mm)
在高雷诺数条件下(Re=100),各裂隙模型(ds=1.0 mm~4.0 mm)在局部区域内(x=50 mm~60 mm)的流线如图8所示。由图8可见,裂隙开度分布随着剪切位移的增加而变化,逐渐形成一个开度先缩小再突然扩张的流动通道,在剪切位移逐渐增加的过程中,首先在裂隙开度扩张区域的下壁面附近形成一个较小的涡流(ds=1 mm),随之涡流面积逐渐增大,同时在裂隙开度扩张区域的上壁面也形成涡流(ds=2 mm),当剪切位移进一步增加时(ds=3 mm~4 mm),上下壁面的涡流区域沿顺流方向逐渐增加扩大,并交替占据裂隙内主要流动通道。
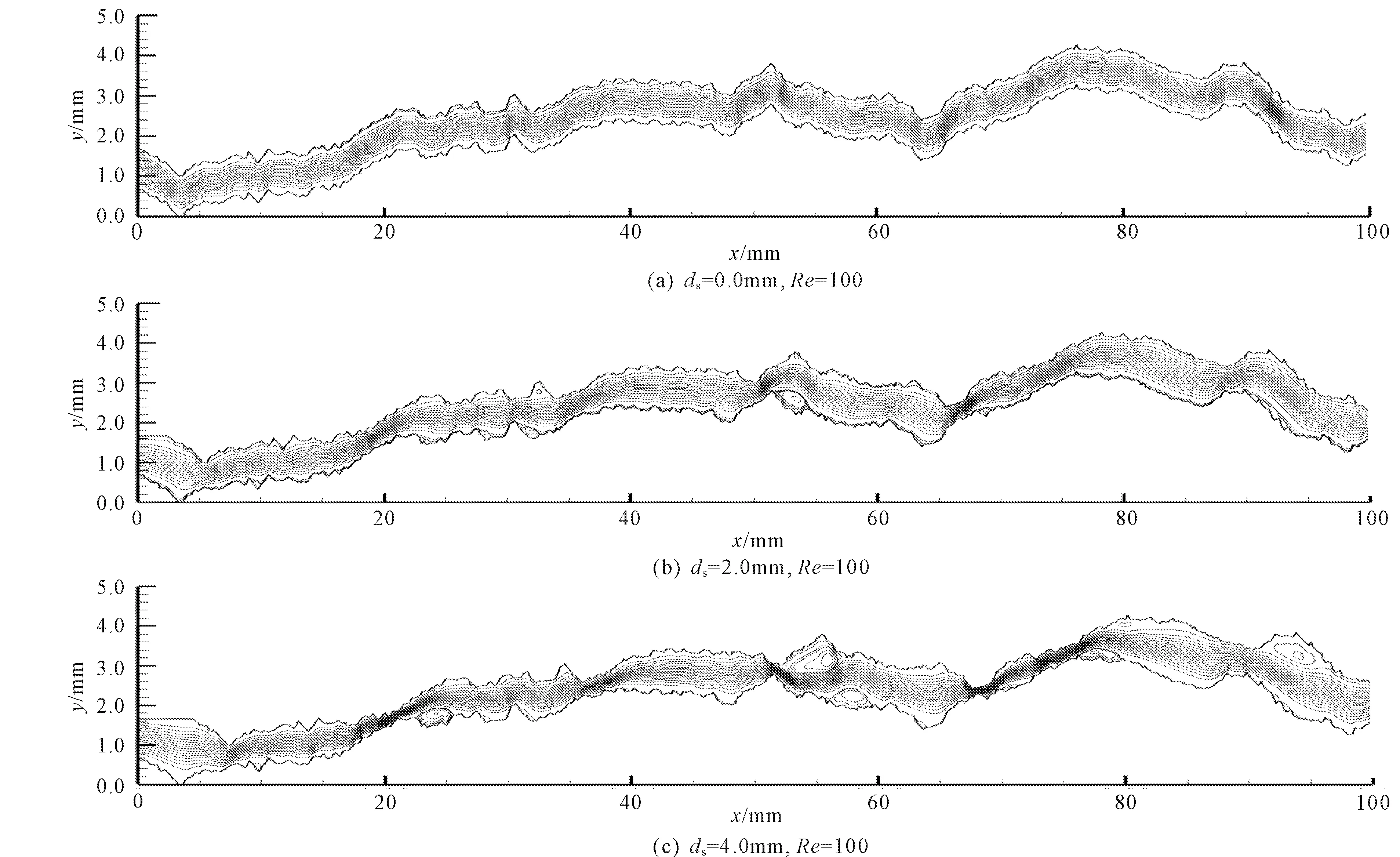
图6 不同剪切位移条件下Re=100.0时流线图
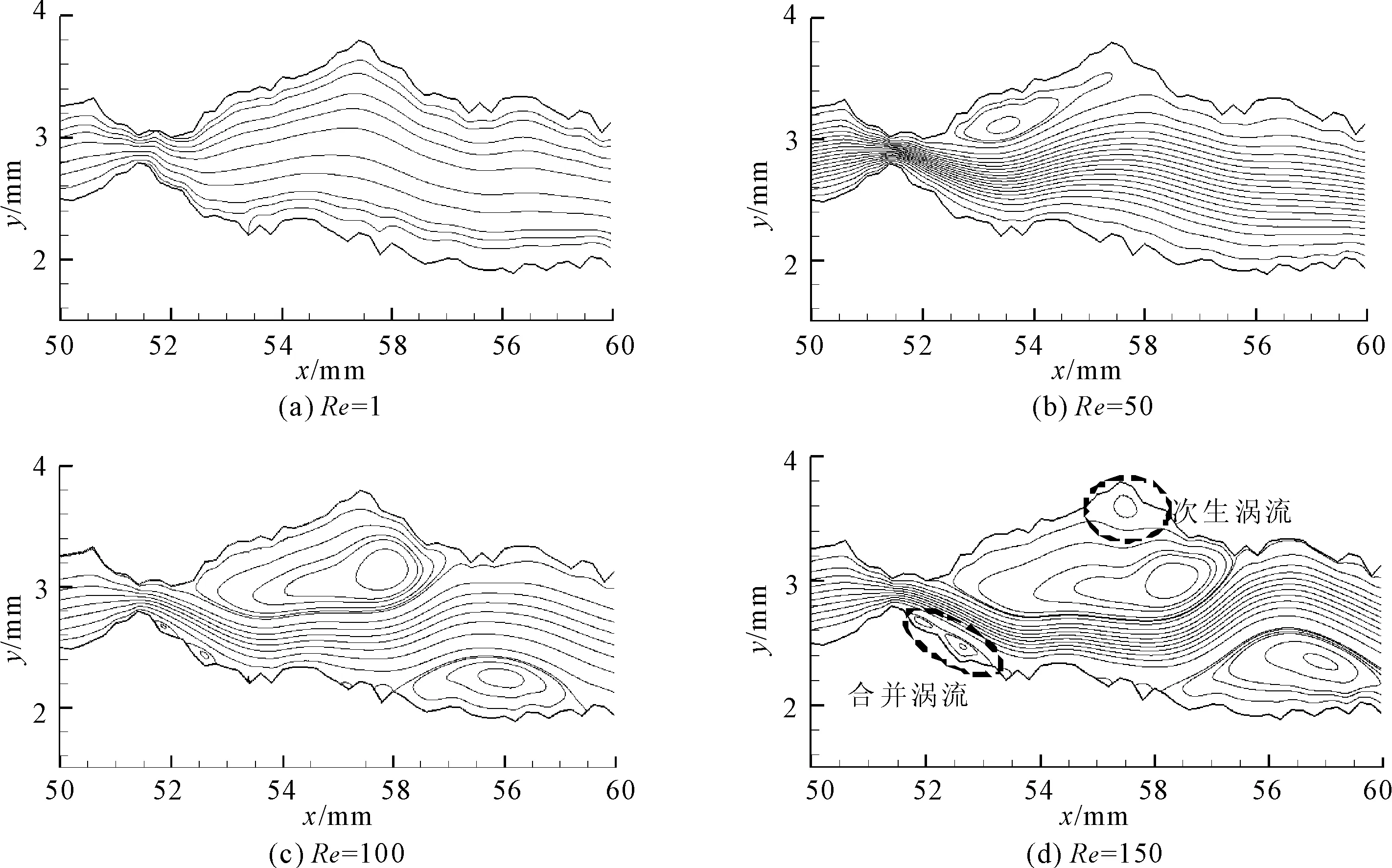
图7 涡流的形成和发展
2.5 水力开度
受涡流的的影响,裂隙内的有效过流面积减小,从而减弱裂隙的过流能力,导致裂隙的等效水力开度降低。各裂隙模型的等效水力开度与平均机械开度比值eh/e随雷诺数Re的变化如图9所示,从图中可以看出,在雷诺数较小时,即Re<1~10,裂隙的等效水力开度基本维持初始的等效水力开度不变,当雷诺数增大时,即Re>10,裂隙的等效水力开度开始逐渐变小,且减小趋势随着雷诺数的增大而增大。同时,对各剪切位移的裂隙模型,裂隙剪切位移越大,裂隙的初始水力开度越小,裂隙的等效水力开度随雷诺数的变化趋势也越明显。
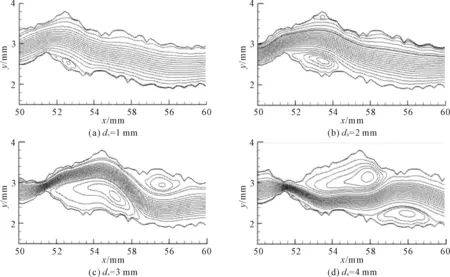
图8 涡流随剪切位移的变化
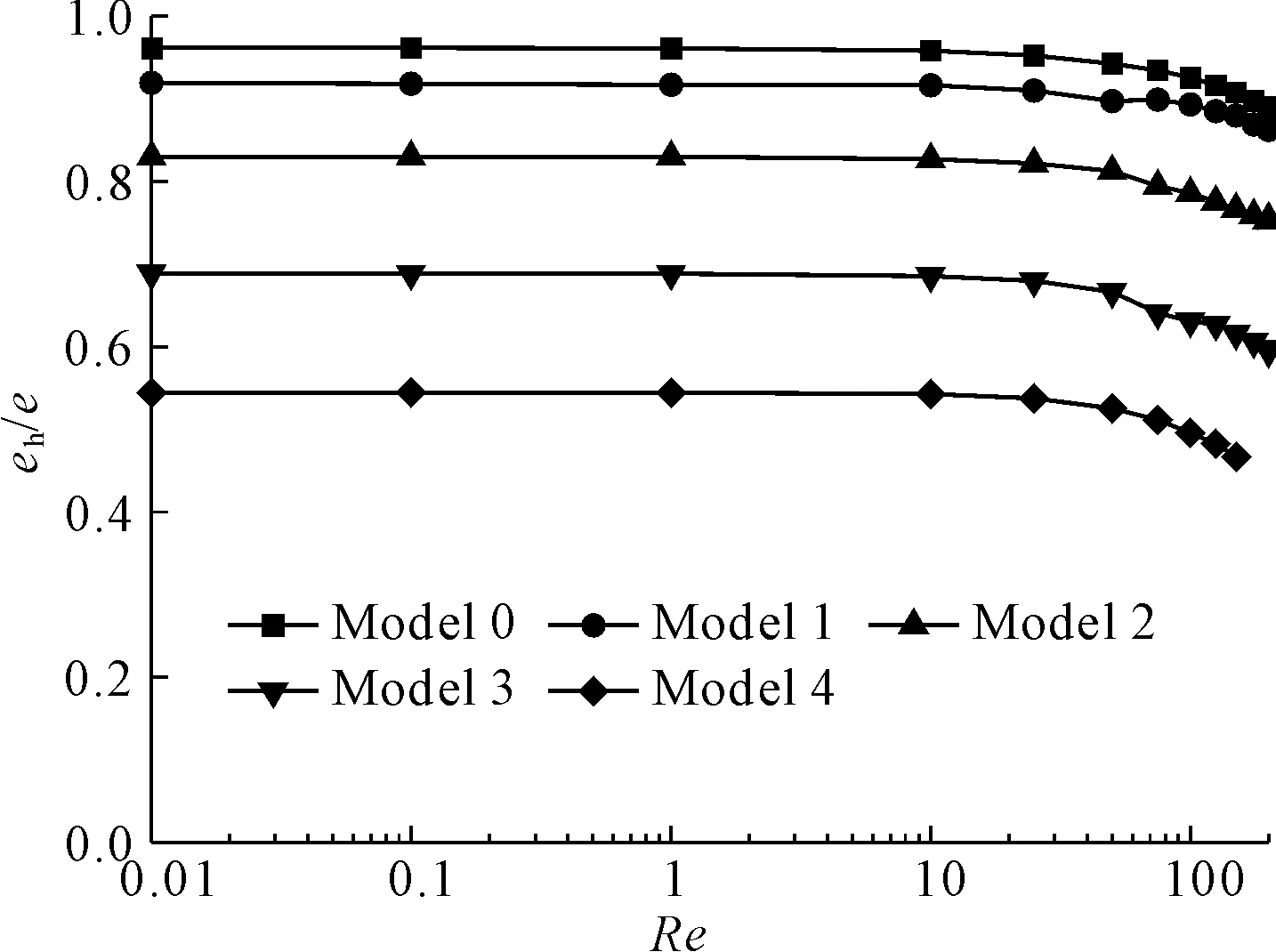
图9 水力开度与平均机械开度比值随Re的变化
3 结 论
本文采用格子玻尔兹曼方法模拟在剪切错动条件下岩石裂隙的渗流过程,考虑不同雷诺数对细观流动特性的影响,主要结论如下:
(1) 发展了裂隙细观流动特性数值模拟的格子Boltzmann方法,并采用圆柱绕流模型验证数值模拟方法的正确性和稳定性。
(2) 数值模拟结果表明剪切错动在高雷诺数条件下可导致裂隙产生明显的非线性流动现象,主要表现为随着雷诺数的增加,在靠近裂隙边壁处低流速区域有所增加,同时出现负方向的流速,说明裂隙内出现明显的涡流区域,且非线性流动随着剪切位移的增加增强。
(3) 数值模拟结果表明在剪切过程中,随着雷诺数的增大,涡流的数量逐渐变多,涡流的范围逐渐扩大,从而导致有效过流通道的减小,裂隙的水力开度减小,且减小的趋势随着雷诺数的增大而增大。
(4) 计算结果揭示了在剪切错动和流速增大条件下裂隙涡流的形成和演化过程,及涡流造成裂隙有效对流区减小、过流能力降低的细观机制,对深化岩土介质渗流和传热过程的认识具有重要意义。
