弹塑性损伤蠕变模型的有限元数值实施

2020-03-30黄文雄

水利与建筑工程学报 2020年1期

崔贤，张涛，黄文雄

(河海大学力学与材料学院，江苏南京 210098)

随着地下洞室开挖、油气储存、核废料处理等项目的增多，软岩流变特性对工程的安全性和稳定性影响已经成为国内外地下工程领域的热点问题，建立能够描述软岩流变特性的本构模型变得至关重要，对于地下工程的变形和破坏的合理预测具有重要的工程意义[1-2]。

国内外学者对软岩的非线性蠕变进行了大量研究，Cristescu等[3]主要研究了岩石的蠕变试验、损伤机理、本构关系以及断裂问题；Adachi等[4]提出了一个可以同时描述软岩硬化和软化的本构模型。Jia等[5]根据泥岩的三轴试验结果，建立了在饱和状态和非饱和状态下都能适用的弹塑性损伤本构模型。在与时间相关性方面，Borja等[6]建立了三维应力状态下湿黏性土与时间相关的本构模型。Shao等[7]提出了一个短期可以描述弹塑性行为，长期可以描述岩石蠕变的本构模型。Hunsche等[8]建立了一个弹黏塑性非线性的盐岩力学模型，该模型可以模拟盐岩的损伤、断裂和膨胀。

肖欣宏等[9]利用Burgers模型和非线性黏弹塑性模型对水环境下红层软岩蠕变进行了研究。贾善坡等[10]在修正Mohr-Coulomb准则中引入了损伤变量建立了反映泥岩软硬化的本构模型。杨春和等[11]通过对盐岩蠕变试验研究，提出了一个盐岩非线性蠕变本构方程。姜永东等[12]根据不同应力水平产生的蠕变差异，建立了砂岩的蠕变本构模型。

ABAQUS材料库中的岩土类模型都是比较经典的本构模型，不能很好地描述软岩流变特性，为了弥补这一不足，利用ABAQUS提供的用户材料二次开发接口，对Shao等[7]模型的进行了有限元数值实施。该模型数学公式简单，参数不多且容易通过基本试验确定，能够描述软岩的三轴试验和体应变特点，并且能进一步考虑软岩的流变特性。采用Fortran语言编写了UMAT子程序，将模拟的结果和试验数据进行对比，进一步验证模型和程序的可靠性。

1 本构模型

本文采用的本构模型[6]包含两部分，即弹塑性模型和考虑塑性损伤的蠕变模型，基础模型描述软岩的短期力学响应，扩展模型能反映软岩在较长时段内的蠕变变形。

1.1 弹塑性模型

基础模型假定材料在应力空间中的屈服面与破坏面相似。采用的强度条件在p-q坐标系(应力平面)的轨迹为抛物线，如图1所示。该模型屈服函数为：

q2+Apr(p-C0)=0

(1)

图1 破坏面和屈服面形态

材料在偏应力作用下的屈服条件采用与强度条件相似的数学表达：

f(p,q,γp)=q2+αp(γp)Apr(p-C0)=0

(2)

式中：αp是硬化变量，依赖于塑性应变。

(3)

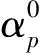
(4)

该模型采用了非关联流动法则，塑性函数采用与原始剑桥模型相似的形式：

(5)

式中：η是另外一个材料参数，该参数确定塑性势面水平切线点连线的斜率；p1是塑性势面与p轴左边交点的坐标(见图2)，与计算塑性应变增量的应力点(当前应力状态)有关。

图2 塑性势面形态

1.2 扩展的弹-黏塑性模型

上述模型经过扩展后，可考虑流变效应，用以预测软岩的长期变形。具体的做法是仿照Pitruszczak等[13]，引进一个时变损伤变量，用于描述刚度和强度随塑性变形发展而下降的规律：

E=(1-αζ)E0,A=(1-α1ζ)A0

(6)

式中：E0是初始杨氏模量，α描述刚度损伤，α1描述强度损伤。

建议的损伤变量演化规律为：

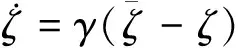
(7)

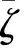
(8)

2 有限元数值实施

利用ABAQUS材料二次开发接口，可将上述模型编成UMAT子程序用于有限元数值分析。数值实施需要在一个典型的时间增量步[tn,tn+1] 上，在已知应力状态σn和应变增量Δε求出的条件下，根据本构关系求出应力增量更新应力，并且给出下一步计算的材料雅可比矩阵。具体如下。

2.1 隐式应力积分回映算法

弹塑性模型的应力积分一般在弹性预测基础上，判断加卸载。对于塑性加载步，本文采用隐式应力积分回映算法，将超出屈服面的应力调整返回到屈服面[8-9](见图3)。

图3 隐式应力积分回映算法示意图

(9)

式中： Δσe为弹性应力增量，De为弹性矩阵。

(10)

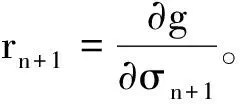
按隐式积分格式，计算塑性应变和内变量增量：

(11)

式中：

(12)

采用牛顿法对非线性方程组(11)求解，在算法的塑性修正阶段中，总应变是一个定值，线性化只有一个变量，即塑性应变因子增量Δλ。

牛顿法中应用如下标记：方程g(Δλ)=0线性化，令Δλ(0)=0：

(13)

式中：δλ(k)是在第k次迭代时Δλ的增量。

为了适应牛顿迭代法，以公式(13)的形式写出公式(11)中的塑性更新变量和屈服条件，省略公式角标n+1:

(14)

线性化后：

(15)

式中：

(16)

(17)

式中：

(18)

由公式(17)可知应力和硬化变量增量：

(19)

将结果(19)代入(15)3求解δλ(k)

(20)

式中：∂f=[fσfαp]

参数更新后：

(21)

多次使用牛顿迭代法，直到结果收敛到更新屈服表面误差范围内。

2.2 一致性切线刚度矩阵推导

应力应变关系为：

(22)

增量形式

(23)

根据流动法则，塑性应变增量

(24)

其中：

(25)

把式(24)代入式(23)得到

(26)

式中：dλ由加载的一致性条件确定

(27)

其中：dαp=(dαp/dλ)dλ依赖塑性应变，dA=(dA/dζ)dζ依赖损伤变量。

对df展开后得到：

(28)

其中：

(29)

把dλ代入式(26)

(30)

式中：

(31)

(32)

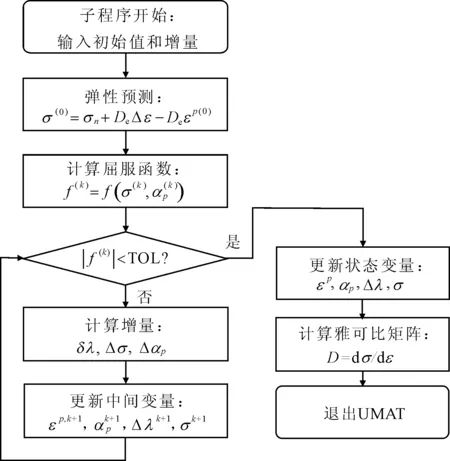
2.3 算法更新流程

第1步，设置初始值。损伤变量ζ是时间的显函数，假定损伤变量ζ=0，利用式(8)，在当前值ζ(t)已知的情况下，对给定的时间增量，利用积分中值定理

θ∈(0,1)

(33)

σ(0)=(1-αΔζ0)σn+DnΔε-Dnεp(0)

(34)

其中：Dn=(1-αζn)De。

第2步，第k次增量步后，检查屈服函数收敛性。

(35)

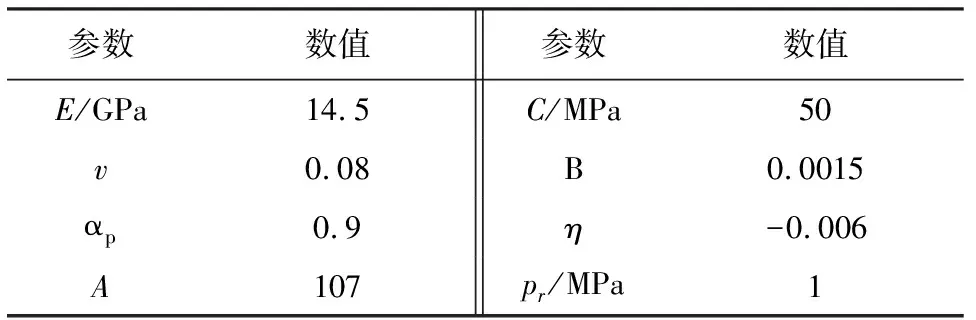
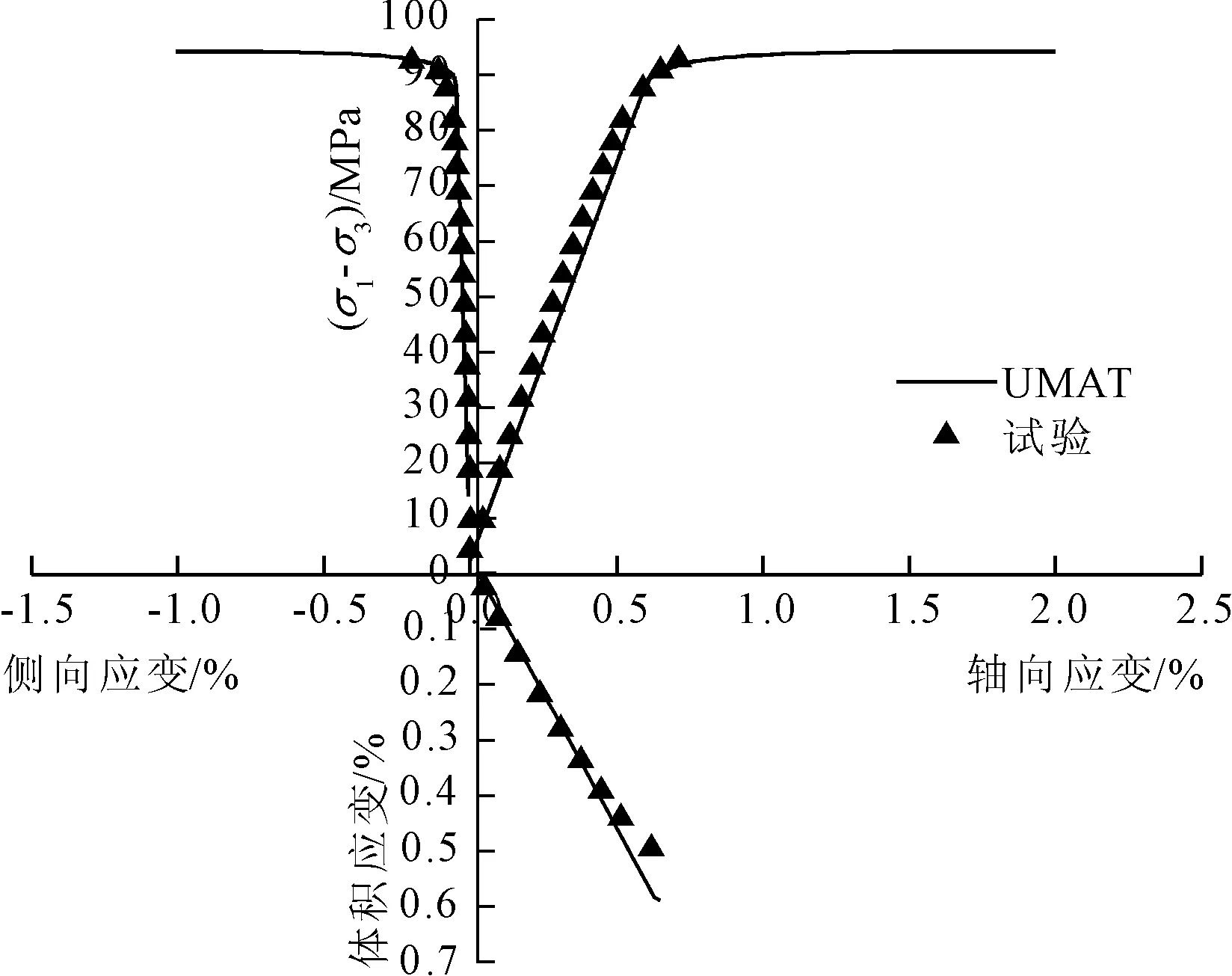
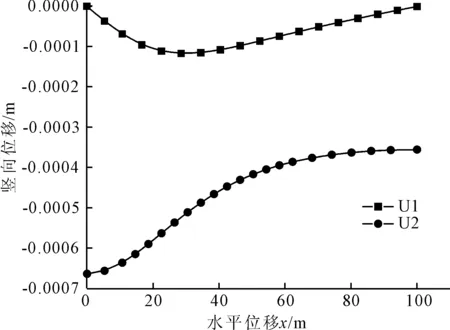
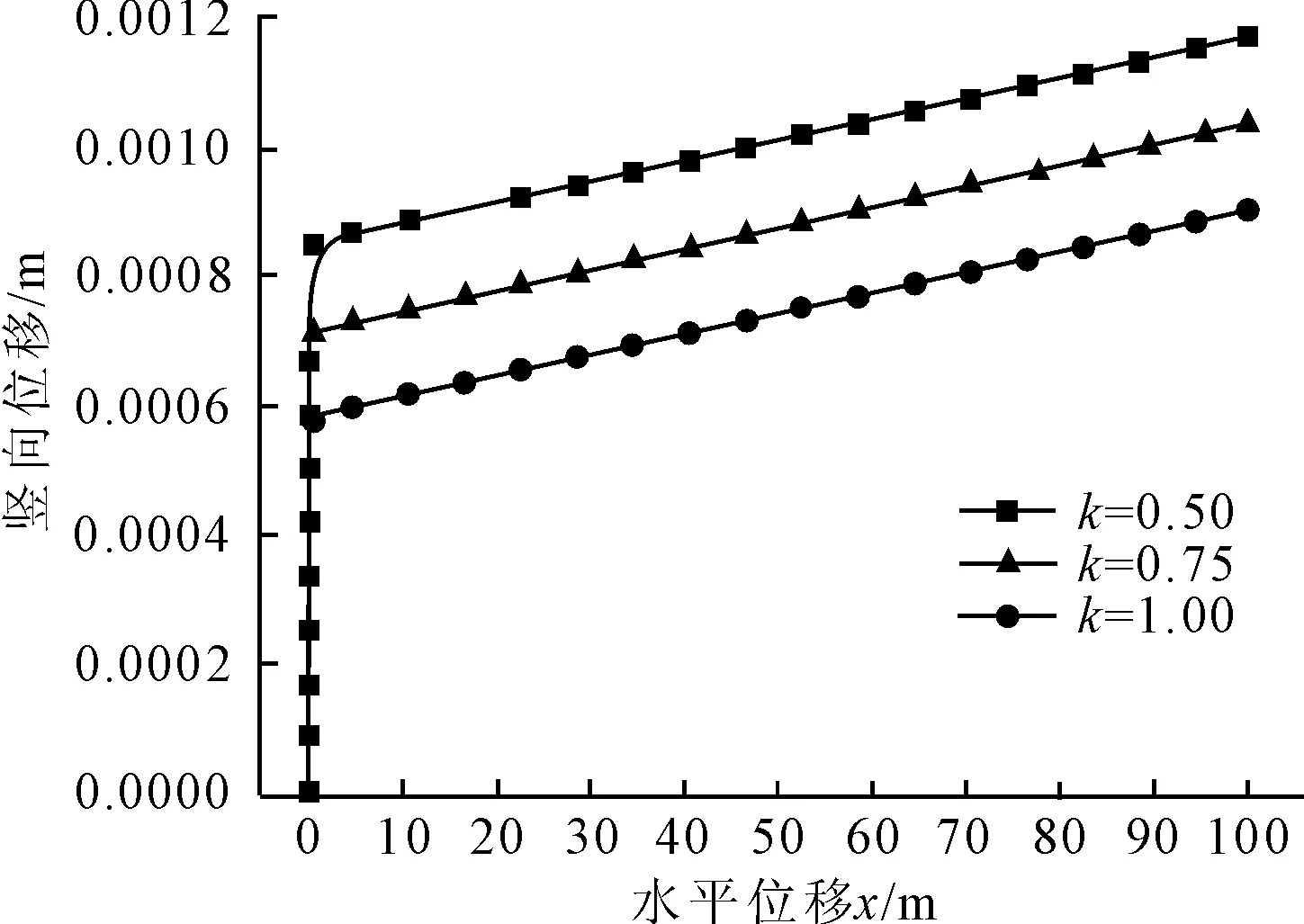
若f(k)

第3步，计算塑性参数的增量。

(36)

第4步，得到应力和硬化变量的增量。

(37)

第5步，更新变量。

(38)

令k=k+1，转到第3步。

3 UMAT二次开发

有限元商业软件ABAQUS提供了UMAT子程序接口[15]，供用户创建自定义材料模型。在增量步开始时，主程序在积分点上调用UMAT，根据传入的应变增量和状态变量，计算出雅可比矩阵(见图4)。

图4 UMAT子程序分析流程图

4 有限元程序验证

利用该本构模型在ABAQUS软件中开发了UMAT子程序，对不同围压下三轴压缩试验和单轴蠕变试验进行有限元数值模拟，将模拟结果与试验结果相比较，用以测试UMAT程序的可行性和准确性。

4.1 不同围压常规三轴压缩试验模拟

常规三轴压缩试验设置了2个围压等级，分别为2 MPa和10 MPa。试验的试样为标准试样(直径50 mm，高100 mm)(模型见图5)，试验加载采用轴向应变控制方式，对试样施加竖向位移2 mm。材料参数见表1。

表1 算例1的模型参数

图6和图7分别为围压2 MPa和10 MPa时的试样应力-应变曲线和体积应变曲线。从图6和图7可以看出，该模型的弹塑性模拟和试验结果有较好的一致性，但是10 MPa围压下的模拟结果比试验结果稍小，原因是在更高的围压条件作用下，材料的之间的孔隙受到压缩变小，使弹性模量变大，导致模拟的结果偏小。材料的体积应变曲线前期的结果与试验比较符合，后期材料进入破坏阶段，出现了小偏离。

图5 三轴压缩试验分析模型

图6 围压为2 MPa时应力-应变和体积应变曲线

图7 围压为10 MPa时应力-应变和体积应变曲线

4.2 蠕变试验模拟

试样模型不变，进行了单轴蠕变模拟，首先在试样垂直方向施加均布荷载力，其值从0 MPa逐渐增加到48.5 MPa,然后保持不变。蠕变模型新增加了三个新参数，取值如表2所示。

图8为单轴压缩蠕变试验模拟曲线，从图8中可以看出，模拟结果和蠕变的试验结果都较为相似，该模型可以表征该类泥岩的蠕变变形性能。

表2 算例2的模型参数

图8 单轴压缩蠕变试验模拟曲线

5 开挖算例

为了进一步验证模型的蠕变特性，建立一个地下无支护洞室对称二维模型，尺寸如图9所示，岩体参数选取依据为上述试验结果，岩体容重2.0×104N/m3，侧压力系数k=0.5，总时间T为100 d，固定左右边界的水平位移和底部边界的竖向位移，对其进行计算分析。

图9 地下洞室模型示意图(单位：m)

图10为开挖后的Mise云图；图11为岩体表面的水平位移和竖向位移图；图12为不同侧压力系数下洞顶位移随时间变化图。由图10可知开挖后的应力变化，右侧顶部和底部的应力比较大，应该作为重点加固区域。从图11可见，靠近中心线的岩体表面处的竖向位移最大，当离中心线距离增大时竖向位移逐渐减小，而水平位移的方向指向中心线，反映了变形方向指向开挖面。为了研究不同侧压力水平对开挖位移的影响，由图12可知，竖向位移随k的增大而减小，不同的侧向应力只对开挖完成时的变形有影响，而后期蠕变的增长趋势保持一致。