考虑渗流影响的基坑变形规律与稳定性研究
2020-03-30何应道
何 应 道
(1.中铁第四勘察设计院集团有限公司, 湖北 武汉 430071; 2.水下隧道技术国家地方联合工程研究中心, 湖北 武汉 430071)
近年来,众多的跨海大桥、深水筑港、大型地铁隧道等工程的建造使中国已经成为了举世闻名的交通大国,我国在沿江、近海等地下水丰富的地区大量修建了穿江过海的公路或地铁等战略性、基础性工程,而这些工程往往需要在高水压、强渗透地层中开挖修建深基坑,会对天然土层的应力场与渗流场造成巨大影响[1-3],使得渗流作用对基坑变形与稳定性影响的研究成为目前工程设计与施工中的难点问题。
国内外在深基坑变形方面研究较多,Ou等[4]采用有限元法进行不排水分析和排水分析研究得出,当基坑工程开挖周期较长时,排水分析较为符合实际情况。Richard等[5]采用数值模拟方法研究得出了粘性土层基坑的各项变形规律特征。刘历波等[6]在进行数值模拟分析考虑地下水的渗流作用得出的深基坑的各项变形模拟结果与监测结果较为吻合。张小伟等[7]通过有限元ABAQUS研究软土地区深基坑的变形情况,研究表明渗流对基坑变形的影响不容忽视。李体康[8]基于渗流应力耦合理论和修正剑桥模型(MCC),结合某工程算例分析了基坑周边的渗流场变化和基坑各项变形,发现没有考虑渗流作用的结果偏于不安全,而考虑渗流合作用能较为准确反映基坑渗流与变形情况。目前,我国对基坑开挖时的渗流场变化和变形情况大都依赖传统简化的经验公式[9-11],对于复杂地质下的工况很难进行更准确的计算,因而渐渐不能满足日益提高的工程要求。柳治富等[12]从土的组成和水动力条件两方面来评价武汉长江隧道工程基坑土体的渗透稳定性,且进一步提出了抵御基坑土体渗透变形的方法和应对措施。曾锃等[13]以某水库大坝反滤层的渗透稳定性研究为例尝试了一种用传统渗流理论确定工程体渗透稳定的薄弱部位,用颗粒分析方法研究其渗透稳定性的新方法。
总的来说,国内外的基坑设计规范考虑渗流影响的不多,而在强渗透地层中,渗流对基坑变形的影响[14-16]不容忽视。而我国现阶段对于强渗透地层的基坑研究还较少,对于强渗透地层中渗流作用的影响与规律还缺乏深入的研究与认识,本文以常德沅江隧道江北明挖暗埋段基坑工程为研究对象,利用流固耦合数值模拟方法,研究不同的土层渗透系数对深基坑变形和基坑底部渗流稳定的影响,得到了一些有益的结论,本研究在工程中具有重要意义和先进性。
1 工程背景及计算模型
1.1 工程背景
常德沅江隧道明挖段基坑根据结构型式的不同可分为敞开段、暗埋段及工作井3部分,基坑总长约560 m(江南明挖段总长290 m,江北总长270 m),基坑开挖深度1.3 m~21 m,基坑宽度为:敞开段约22 m,暗埋段约28 m~35 m,工作井宽34 m~36 m。其中,含水圆砾层透水性强,渗透系数最大可达6×10-4m/s,且距离沅江较近,基坑侧壁涌水量很大。沅江隧道江北里程YK0+270—YK0+370段为明挖暗埋段,考虑到基坑计算的典型性,在本次研究中选取降水开挖施工段YK0+336—YK0+370为研究对象,深度约12 m。其场地上部杂填土厚在4 m左右,粉土层厚在4 m左右,其下圆砾层厚超过80 m左右,其间粉细砂夹层厚在8 m左右。
1.2 计算模型
采用有限差分软件FLAC3D建立基坑模型,如图1所示,基坑长度(x轴)为29 m,宽(y轴)14 m,z方向为地连墙嵌入深度方向,地连墙厚度为1 m,实际计算中为简化问题,利用对称性只建立四分之一的基坑模型。地连墙和内支撑采用线弹性模型,土体采用摩尔-库仑模型,基坑各土层物理力学参数如表1所示。监测布置如图1所示,C1—C16为基坑墙后地表沉降监测点,L1—L14为基坑隆起竖向位移监测点,Y1—Y35为地连墙侧向位移监测点。土体的渗透系数是影响渗流作用大小最重要的因素之一,而基坑底板以下的深厚圆砾层属于强渗透地层,渗透系数达到6×10-4m/s,为了研究强渗透地层渗透性质对渗流作用的影响,本文以圆砾层的渗透系数为基准值,取该基准值的0.5倍(3×10-4m/s)、2倍(12×10-4m/s)分别进行对比分析。

表1 土层物理力学参数
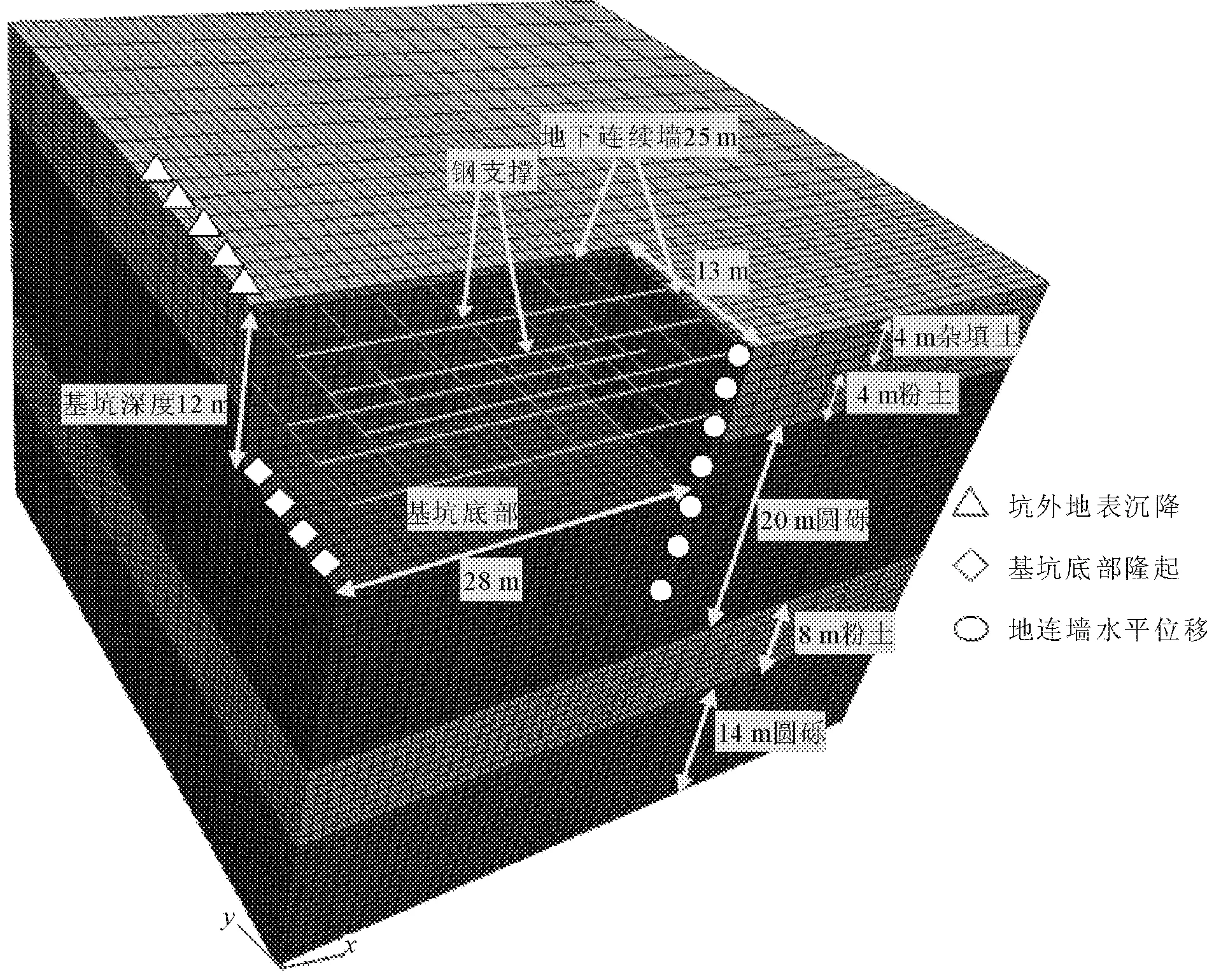
图1 监测点布置示意图
2 结果分析
本次计算结果见图2—图4、表2。图2为三种不同土体渗透系数的深基坑开挖完成后的基坑底部隆起曲线。可以发现三种情况下基坑底部隆起变形规律是基本一致的,测点在地连墙处基坑隆起量最小,距连续墙1 m处隆起量显著上升,三种不同土体渗透系数的基坑底部隆起量均在基坑中心处最大。当土体的渗透系数为12×10-4m/s时,最大值为184.08 mm,而当土体的渗透系数为6×10-4m/s和3×10-4m/s时,二者的基坑底部隆起量近乎相等,最大值分别为88.45 mm和85.34 mm,前者的基坑底部隆起量约等于后两者的2倍。说明当渗透系数减小时,基坑底部的隆起值会随之减小,且变化量较大,但当土体渗透系数继续减小到一定值时,则对基坑底部的隆起变形几乎没有影响。
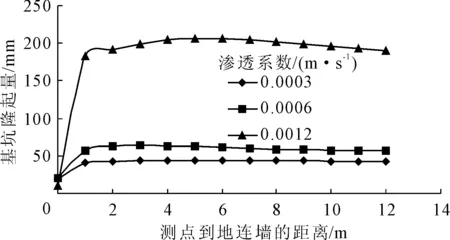
图2 土体不同渗透系数下的基坑底部隆起量
由图3可见,不同渗透系数的墙后地表沉降曲线的整体变化趋势是一致的,皆呈勺子状,最大沉降均在基坑外17 m至22 m左右,距地下连续墙约34 m后基坑开挖对墙后地表沉降几乎没有影响。随渗透系数增大,其最大沉降值约为62.25 mm、81.46 mm和85.58 mm,量值相差并不明显。
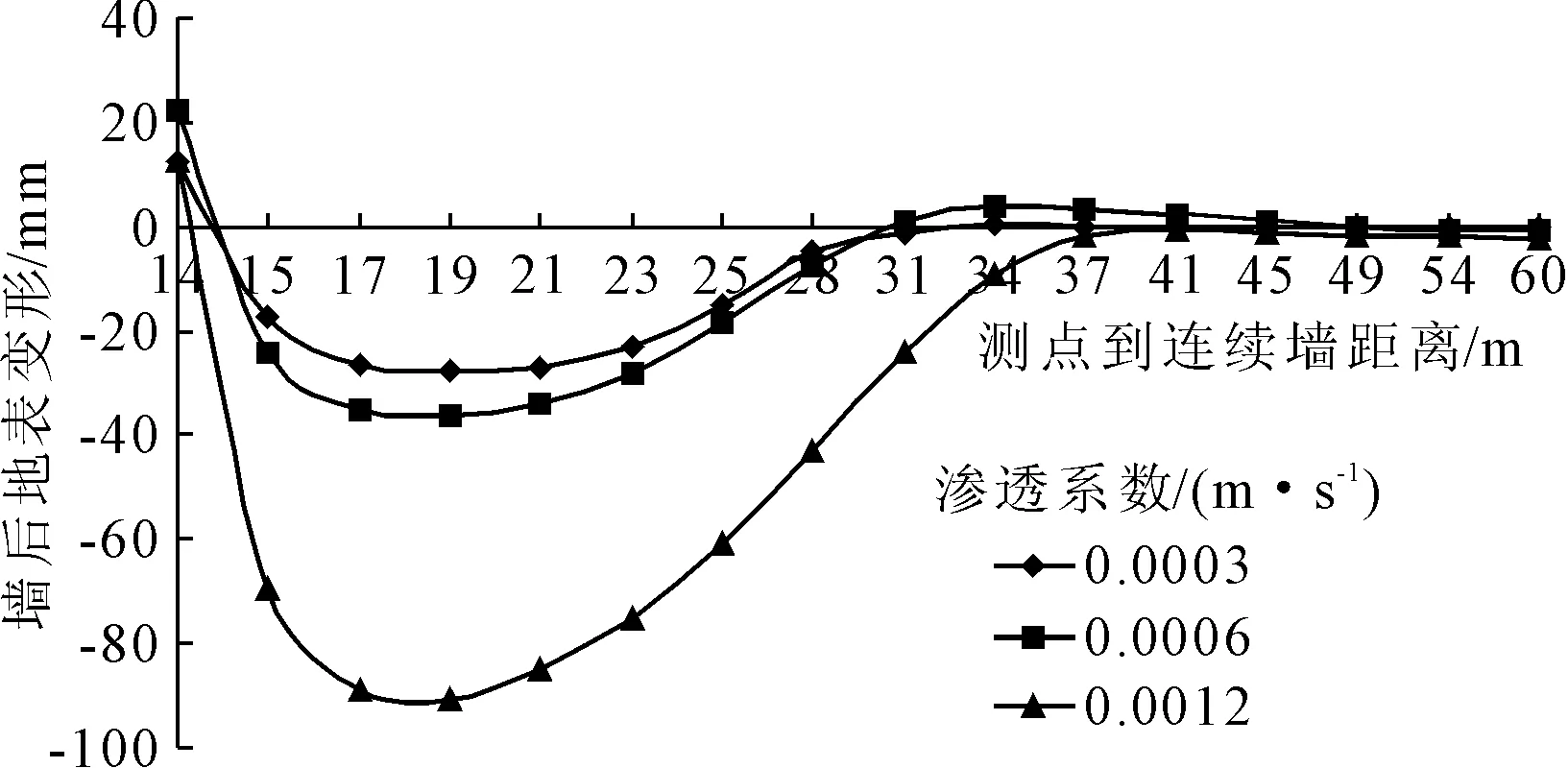
图3 土体不同渗透系数下的坑外地表沉降
图4为不同渗透系数条件下的地下连续墙水平位移变化曲线。根据图4的曲线变化趋势,可以发现当渗透系数为12×10-4m/s时,连续墙水平位移最大值为95.38 mm,而当渗透系数为6×10-4m/s时,连续墙水平位移最大值为92.23 mm,而当渗透系数为3×10-4m/s时,连续墙水平位移最大值为82.95 mm。总之,随着土体的渗透系数增大,其水平位移随之增大,但变化量不大。
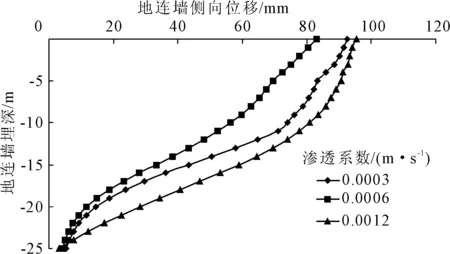
图4 土体不同渗透系数下的地连墙水平方向侧向位移
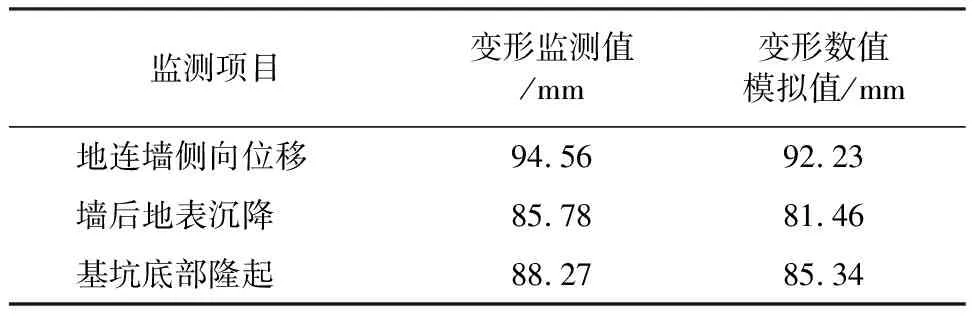
表2 数值模拟最大值和监测最大值对比
表2列出了渗透系数6×10-4m/s时基坑各项变形的数值模拟最大值和相应部位的监测值,通过对比可知,考虑渗流作用的基坑变形数值结果与实际的监测值比较吻合,说明本文建立的数值模型与采用的计算参数是基本合理的,可以适用于强渗透地层的流固耦合计算。通过对基坑变形结果的分析,可以发现随着土体渗透系数的增大,基坑降水开挖所引起的地连墙水平位移、墙后地表沉降和基坑底部隆起值均有所增加。且渗透系数的变化对基坑底部隆起的影响较大,对墙后地表沉降和地连墙水平位移的影响较小,当渗透系数达到某一阈值之后,基坑底部隆起量陡升,量值相差较大,原因可能是由于高水压直接作用于基坑底板处的强渗透圆砾地层,随渗透性增大,圆砾层发生了由稳定渗流到非稳定渗流的质变。
到现在为止,相关国家基坑规范和手册[17]大都是假定稳定渗流条件下来评价基坑底部抗渗流能力的强弱,规范中指出,基坑渗流的临界水力坡降与实际水力坡降之比应大于工程所规定的安全系数,如式(1)所示:
m≤icr/i
(1)
式中:m为基坑底部抗渗流能力的安全系数;i为实际水力坡降;icr为临界水力坡降,icr=γ′/γω,γ′为土体浮重度;γω为地下水的重度1.0×104N/m3。
根据式(1),图5给出了不同渗透系数条件下的基坑底部安全系数变化曲线。如图5所示,当考虑渗流作用时,圆砾层的渗透系数越大,基坑底部安全系数呈十分明显的下降趋势;当不考虑渗流作用时,基坑底部安全系数随渗透系数的变化趋势较为平缓。相对而言,基坑底部中心处的安全系数均大于基坑底部坑角处的安全系数,在实际工程中,基坑底部坑角处的渗流稳定问题应更加引起重视。
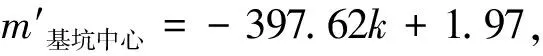
不考虑渗流作用影响时,二者之间的关系分别为:m基坑中心=-73.81k+1.94,m基坑坑角=-83.83k+1.92。
根据数学方法可拟合考虑渗流作用时基坑底部处的安全系数与规范中不考虑渗流作用时基坑底部处的安全系数之间的函数关系为:m′=5.38m-8.48。
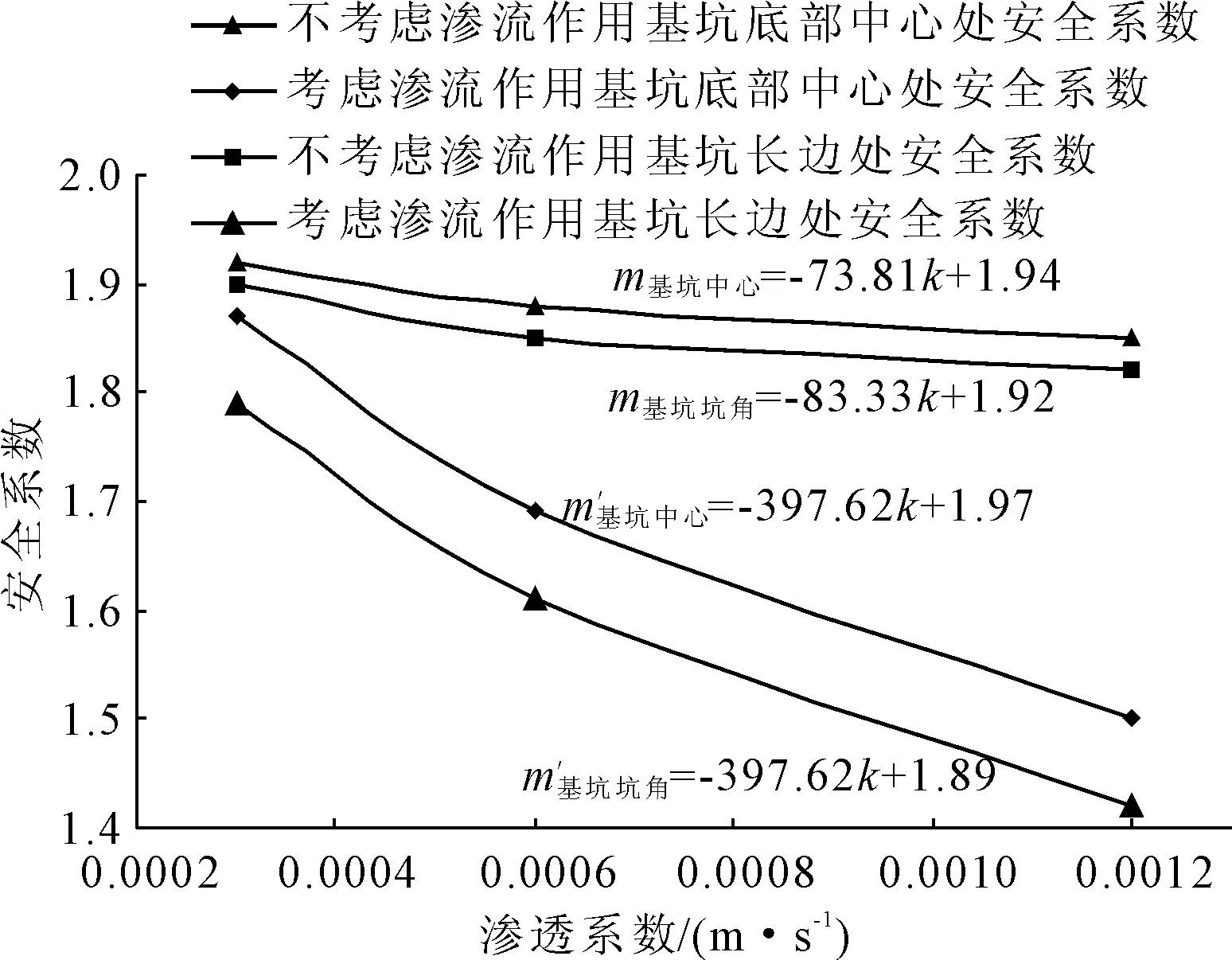
图5 土体不同渗透系数下的基坑开挖后基坑底部的安全系数
3 结 论
(1) 当考虑渗流作用时,基坑各项变形的模拟计算数值与实际工程的监测结果十分相近,说明本文建立的数值模型与采用的计算参数是基本合理的,可以适用于强渗透地层的流固耦合计算。
(2) 考虑渗流作用时,圆砾层的渗透系数越大,基坑底板安全系数呈十分明显的下降趋势;当不考虑渗流作用时,基坑底部安全系数随渗透系数的变化趋势较为平缓。
