对建筑复合地基面积置换率问题的探讨
2020-03-30宫志张龙
宫志,张龙
(安徽省交通规划设计研究总院股份有限公司公路交通节能环保技术交通运输行业研发中心,安徽 合肥230088)
0 前言
在复合地基处理中,置换率是一个非常重要的基本概念,即竖向增强体的横断面积与其所对应的复合地基面积之比,《建筑地基处理技术规范》(JGJ 79-2012)通过引入等效圆直径的概念,规定了正方形、矩形及正三角形等规则布桩时的置换率的计算公式,但是对于公式的适用条件以及非规则布桩时是否适用并没有一个明确的解释,使得工程应用上错用、乱用规范公式情况比比皆是。本文将从置换率基本概念的定义出发,介绍置换率求解的基本方法,并推导规范中单桩型复合地基三种布桩形式等效圆置换率公式及适用条件,并修正规范中多桩型复合地基置换率公式的错误,为以后的工程应用提供一定的参考。
1 复合地基置换率的计算分析
置换率定义为竖向增强体的横断面积与其所对应的复合地基面积之比;在实际工程应用中须严格遵守这一基本概念,使用置换率普遍基本公式m=A/Ae来计算。式中A为桩体面积,Ap为桩体分担的地基处理面积。
对于有限范围内(如独立基础内)布桩时,可根据置换率的定义按照有限范围内所有桩的面积除以有限范围的总面积即可得到置换率。即

式中Ap为单根桩的截面积,A为有限范围的总面积。
但对于大面积地基处理的情况,按照定义求得地基处理总面积及所有桩总面积并不现实也非必要,可以用划分单元体的方法来求解。单元体的划分原则为大面积必须全部由无限个相同的单元体组成且每个单元体内桩数必须一样。单元体内桩身面积与单元体面积之比即为置换率。单元体的划分并非唯一的,可以有多种不同的划分方式。
1.1 梅花桩布置时

按单元1划分时,此时单元体1面积内桩的截面积为两根桩+四个四分之一桩+两个二分之一桩:

按单元2划分时,此时单元体2面积内桩的截面积为两个二分之一桩:

按单元3划分时,此时单元体3面积内桩的截面积为一根桩:


式中d为单根桩的直径。
1.2 条形基础下双排布桩时
按单元1划分时,此时单元体1面积内桩的截面积为四个二分之一桩:

按单元2划分时,此时单元体2面积内桩的截面积为两根桩:

式中d为单根桩的直径,b为条形基础的宽度。
从上可知,对于大面积复合地基处理,虽然单元体的划分方式多种多样,但是每一种单元体最终计算的置换率是相同的,由此可见,对于大面积复合地基处理的情况,用划分单元体的方法计算置换率是十分方便的,但对于譬如独立基础等有限范围内的布桩时,使用划分单元体计算置换率是错误的,应按照m=nAp/A来计算。
首先,变压器的使用方面。减少变压器的无功损耗,合理选择变压器的负载率。变压器的节能体现在装设无功补偿、降低空载损耗和负载损耗几方面。提高变压器的系统功率。具体的实施方案为改进变压器的铁心制造工艺,选用低损耗的变压器;适当减少线圈数和绝缘面积,提高填充系数;当变压器使用量需求较大,需要的容量增大时,要设置静电电容器进行无功补偿。不能一味的追求变压器的容量,而忽视变压力的负载率。要根据实际需要对变压器的负载率进行合理的选择。
2 规范中等效圆面积置换率公式的推导
《建筑地基处理技术规范》(JGJ79-2012)规定桩土面积置换率按照m=d2/d2e来计算,

式中d为桩身平均直径,de为一根桩分担的处理地基面积的等效圆直径,其中等边三角形布桩时:de=1.05s;正方形布桩时:de=1.13s;矩形布桩时
2.1 等边三角形布桩时
按图示划分单元体,此时单元体面积内桩的截面积为半个桩面积:

故等边三角形布桩时de=1.05s。
2.2 正方形布桩时

按图示划分单元体,此时单元体面积内桩的截面积为一个桩面积:

故正方形布桩时de=1.13s。
2.3 矩形布桩时

按图示划分单元体,此时单元体面积内桩的截面积为一个桩面积:

置换率本质是面积的比值,规范通过人为的引入一个等效圆,用直径的平方比来计算置换率,反而使置换率概念变得复杂且不易理解,此公式只适用于大面积规则布桩形式(正三角形,正方形,矩形等),当布桩形式不是规范给出的三种形式时,而是等腰三角形、梯形或其他不规则布桩形式时,或者有限范围地基处理时,规范公式并不适用,具有一定的局限性,只能使用置换率普遍基本公式m=A/Ae来计算。
3 多桩型复合地基置换率的计算分析
多桩型复合地基面积置换率,应根据基础面积与该面积内实际布桩数量进行计算,即m=nAp/A,当基础面积较大或条形基础较长时,即大面积地基处理时可用单元面积置换率替代。
《建筑地基处理技术规范》(JGJ79-2012)给出了大面积多桩复合地基时三角形和矩形布桩的置换率公式,可按照前述单元体划分原则来推导。
3.1 矩形布桩时

取单元体为图示小正方形,一个单元体面积内有桩1两根,桩2两根,设桩1面积为Ap1,桩2面积为Ap2,正方形面积为4s1s2,桩1和桩2的面积置换率分别为:

3.2 三角形布桩且时
当时,规范给出的桩1和桩2的面积置换率分别为:

取单元体为图示小正方形,一个单元体面积内有桩1两根,桩2两根,设桩1面积为Ap1,桩2面积为Ap2,正方形面积为当 s1=s2时,桩 1和桩2的面积置换率分别为:
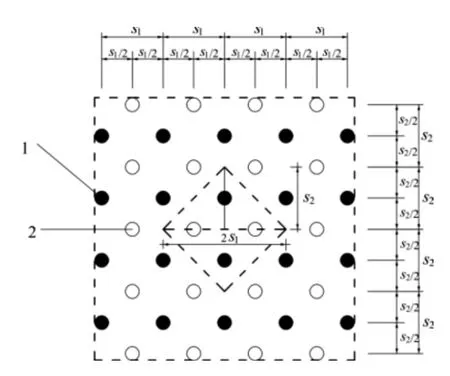

由此可见,《建筑地基处理技术规范》(JGJ79-2012)第7.9.7条第二款给出的三角形布桩的置换率公式有误。
4 结语
本文通过置换率基本概念的定义,介绍不同情况下不同布桩形式置换率求解的基本方法。
结果表明,对于有限面积内置换率的求解,只能根据基础面积与该面积内实际布桩数量进行计算,即m=nAp/A;对于大面积内置换率的求解,可以通过划分单元体的方法按照m=A/Ae来计算。而规范中引用的计算置换率的等效圆法,仅适应于大面积复合地基时且布桩形式为正三角形、正方形和矩形等三种形式。
通过对大面积多桩复合地基时三角形和矩形布桩的置换率公式的推导,更正了规范中三角形布桩时置换率公式的错误之处,为以后的工程应用提供一定的参考。
