一种固体小运载火箭弹道优化研究方法*

2020-03-30李晓晖程养民

弹箭与制导学报 2020年5期

薛杰,李晓晖,程养民

(西安航天动力技术研究所固体火箭发动机燃烧、热结构和内流场国防科技重点实验室, 西安 710025)

0 引言

近年来,随着小卫星和“空间快速响应”技术的快速发展和火箭设计、复合材料、电子技术以及固体推进技术的发展,将微小型固体运载火箭推上了航天发射的大舞台[1]。微小型固体运载火箭采用固体发动机,其具有发射成本低、反应速度快、适应能力强等突出特点[2]。因此为减小成本,需在给定入轨条件和发动机推力的条件下进行弹道优化。

文中通过对仿真模型的验证,发现模型搭建完好,接着进行弹道优化。将优化后的弹道与基本方案进行对比。从而最终获得了使卫星快速、准确入轨的弹道约束条件下,可以发射最大有效载荷的弹道。

1 某运载火箭简介

运载火箭采用三轴稳定的四级方案,由四级固体动力、控制系统、箭体结构、箭上遥测、安控等系统组成,如图1所示。

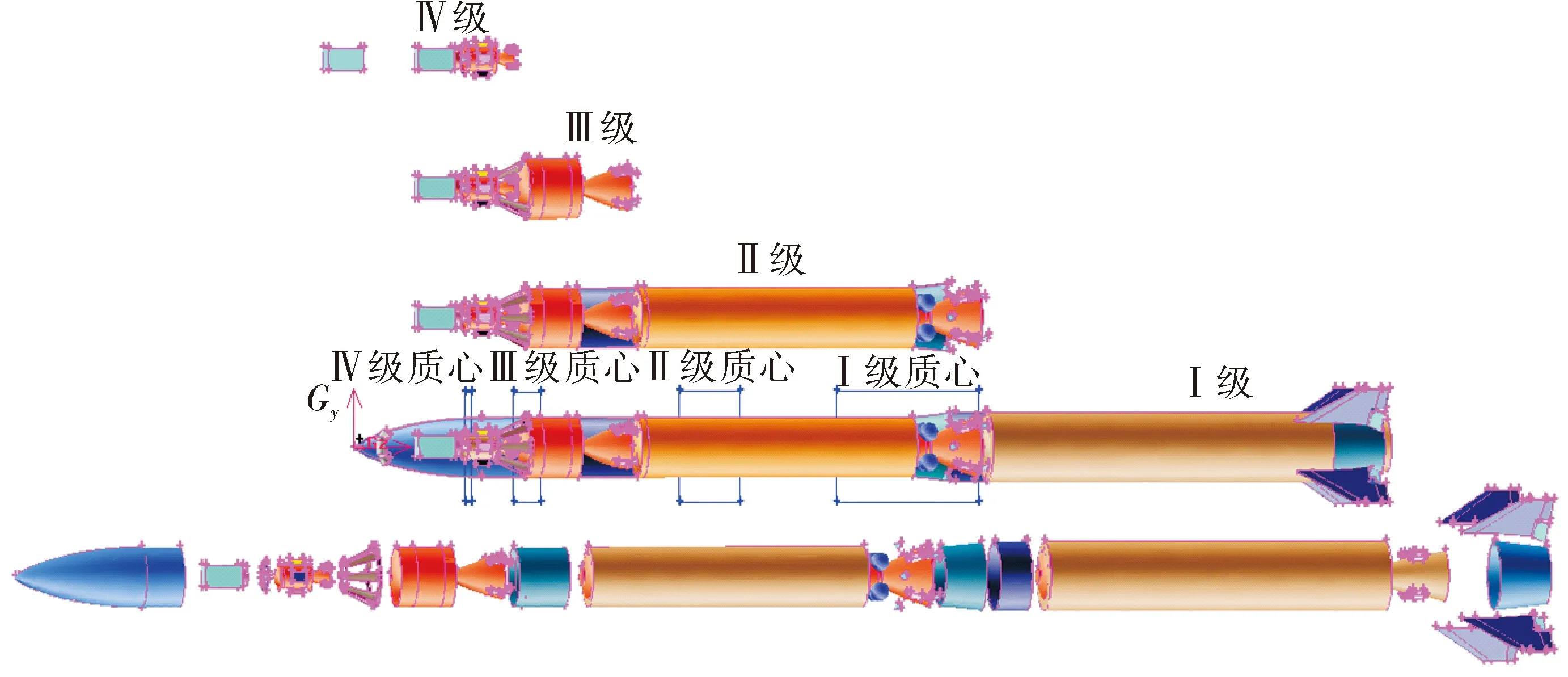
图1 运载火箭的四级示意图

利用Matlab软件的Simulink模块进行运载火箭仿真建模[3-5],所用方程参考文献[6-9]。运载火箭入轨条件:轨道高度为500 km的椭圆轨道;入轨速度大于7 700 m/s。

2 优化模型

选用伪谱法进行弹道优化,对其进行离散形式的展开,从而可进行数值优化,得到最优控制问题的解。接下来从优化参数、目标函数以及约束条件建立优化模型。

弹道优化问题可以表示为一般的最优控制问题,即寻找合适的控制变量u(t)∈Rn,使式(1)所示的Bolza型性能指标在满足动力学微分方程约束、路径约束和边界约束的条件下达到最小化,即

(1)

其中,u(t)∈Rn为控制变量;x(t)∈Rn为状态变量;t0和tf为时间初值和末值,可固定可自由。系统要满足动力学微分方程约束、边界约束以及路径约束分别如式(2)、式(3)和式(4)：

(2)

φ(x(t0),t0,x(tf),tf)=0

(3)

C(x(t),u(t),t)≤0,t∈[t0,tf]

(4)

基于在发射坐标系下建立的六自由度弹道模型对弹道进行优化。

2.1 目标函数

固体运载火箭弹道优化的目的是减小发射成本,提高火箭的运载能力,即给定条件下产生最大有效载荷。文中研究的运载火箭采用三轴稳定的四级方案,且各级固体发动机燃料都会全部耗尽,属于耗尽关机的工作模式,优化实质即为有效载荷质量mp最大。其有效载荷为星箭分离后卫星的总质量。因此,选取的目标函数为:

minJ(u)=-mp

(5)

2.2 约束条件

运载火箭的弹道优化约束条件有两种:边界条件和路径约束条件。

1)边界条件

初始位置(0,0,0)和初始速度(0)已知。终端入轨条件选取轨道高度Hf和入轨速度vf,其取值范围为：Hf≥500 km,vf≥7 700 m/s。

2)路径约束

运载火箭在运动过程中要保证结构完整性以及相关电子设备的正常使用,其要求为:最大轴向过载约束不大于20g,考虑火箭与大气间产生大量的热会给外壳带来危害,则最大动压约束不大于1 MPa。

2.3 优化参数

优化参数选取飞行时序中一些重要参数:垂直起飞时间、程序转弯时间、程序转弯角度和三级滑翔时间。取值如表1所示。

表1 飞行时序各优化参数的取值限制范围

2.4 优化算法设计

伪谱法是一种求解最优控制的工程方法,经离散后将最优控制问题转化为NLP问题,通过有效大规模稀疏NLP求解器求解。

采用基于伪谱法进行运载火箭弹道优化设计算法时,计算步骤如下:

1)网格区间初始化,确定初始迭代时区段数量K和区段插值多项式M。

2)计算全固体运载火箭各个约束条件的约束函数误差。

3)当ek，max≤εd时,说明对应区段精度满足各约束,如果所有区段的精度均满足约束条件时,则求解完成,可优化出最优弹道。

5)检查所有区段的精度是否满足精度要求εd,如果满足精度要求,则结束运算;如果不满足精度要求,则返回到步骤1)重新开始循环计算,直到满足精度εd为止。

3 优化结果分析

在优化模型中利用高斯伪谱法优化得到最优解,此时综合了各参数的影响因素,故该最优解具有全局性。

按照前述的优化模型,通过高斯伪谱法进行计算,得到最终优化后的某型全固体运载火箭的飞行弹道,与优化前的弹道进行对比分析。最终优化前后的各优化参数如表2所示。

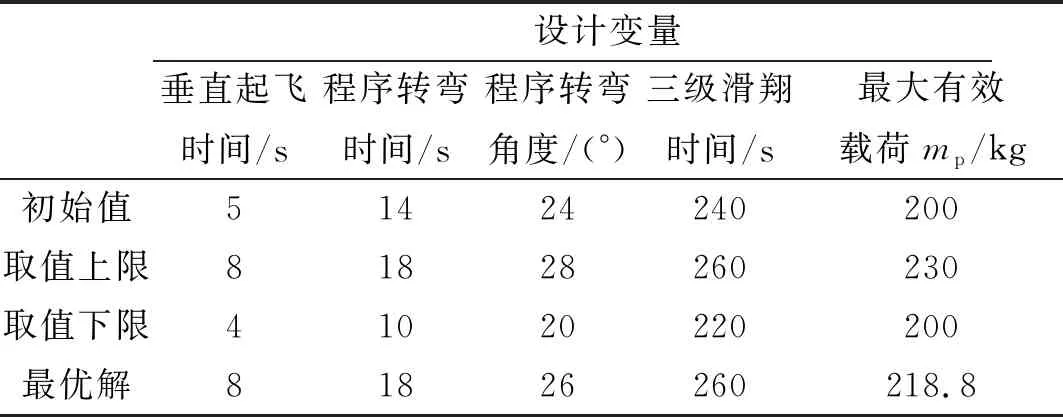
表2 最终优化设计结果

飞行高度和速度是运载火箭入轨所必需的条件之一,但这些数值并不是越大越好,满足入轨条件即可。

终端入轨条件为Hf≥500 km,vf≥7 700 m/s。

首先需要满足入轨高度和速度,这是保证小型卫星顺利送入预定轨道的基础。经过计算优化,观察火箭的高度和速度变化规律,优化前后运载火箭的高度和速度随时间的变化如图2和图3所示。

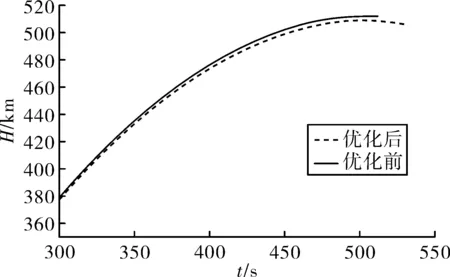
图2 优化前后火箭当地高度时间图像

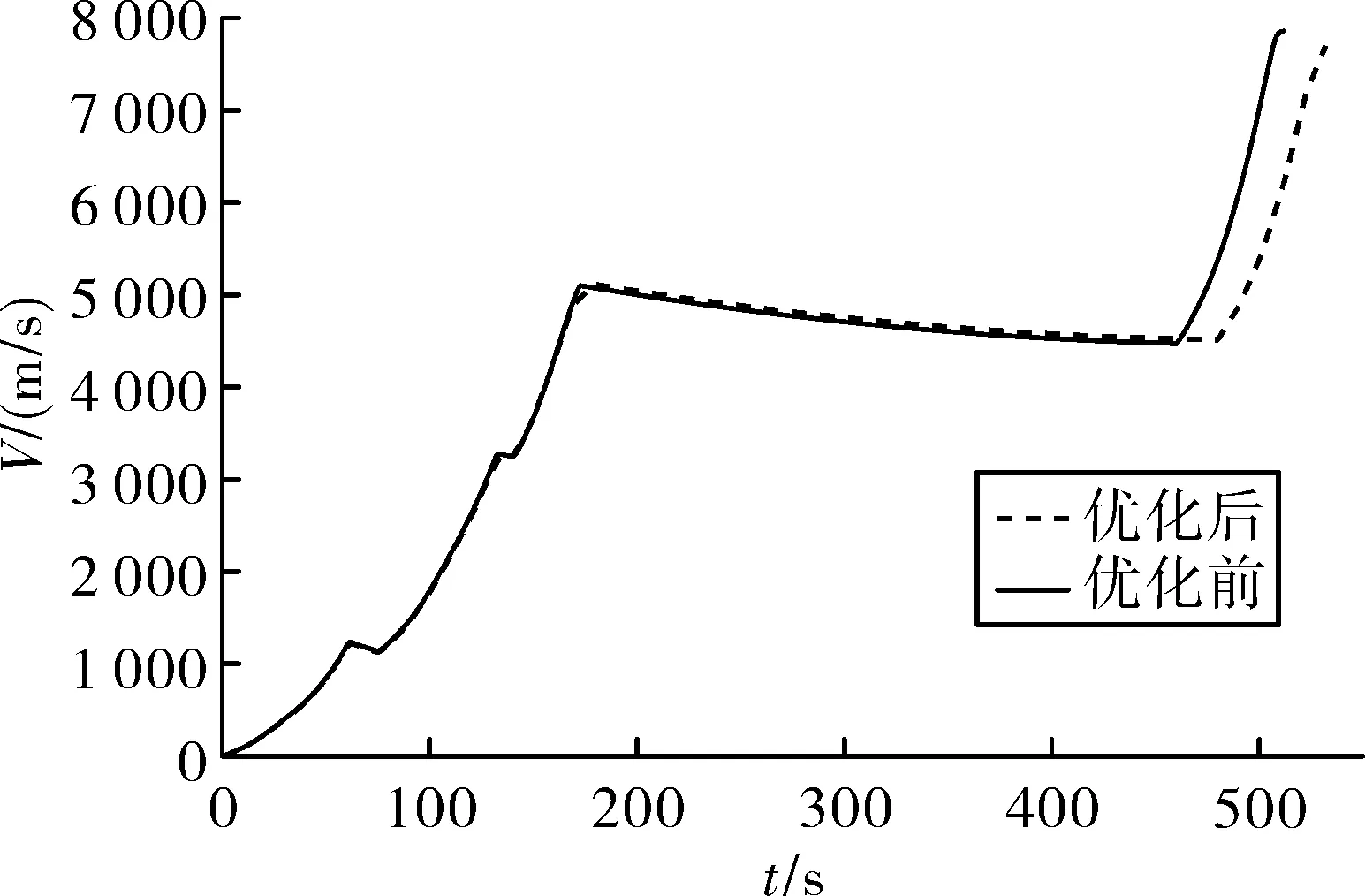
图3 优化前后火箭相对速度时间图像

优化前后高度和相对速度的变化趋势大致相同。由于要使卫星快速精确入轨,通过图2可看出：优化后当地高度更接近入轨高度,数值为502.3 km,更能精确入轨,而且可将富裕的能量补充更多有效载荷,从而可使火箭有效载荷更大。通过图3发现：优化前后一二三级的相对速度随时间变化不大,仅受三级滑翔段时间的增加使火箭的速度有所变化,最终经四级固发再加速,使火箭达到所需的入轨速度,数值为7 701.6 m/s。

在运载火箭四级发动机推力给定的条件下,通过高斯伪谱法进行优化模型的计算,最终调整飞行时序及滑翔时间。

四级发动机推力时间图像如图4所示。

图4 优化前后火箭发动机推力时间图像

由于四级全固体发动机的特性,所以其各项性能参数如发动机质量、开关机时间和瞬时推力已确定。因此优化前后几乎不变,仅推力加载时间点受飞行时序的影响。

优化前后运载火箭的质量时间图像如图5所示。

图5 优化前后火箭质量时间图像

从图中可看出：在前450 s,优化前后的火箭质量重合,这是由于运载火箭总体质量很大,而优化后仅比优化前有效载荷提高18.8 kg,450 s之后由于三级滑翔时间的不同使两条曲线区分开。运载火箭的质量变化趋势在优化前后一致,同时也提高了运载火箭的有效载荷,说明优化方法是较为合理的。

优化时,在最大有效载荷对应的优化参数下,固定此参数值,通过改变有效载荷的大小得到飞行速度与有效载荷的变化图像如图6所示,飞行高度与有效载荷的变化图像如图7所示。

通过图6可以看出：随着运载火箭的有效载荷增大,火箭的飞行速度随之减小,基本上是一条直线。所以在入轨速度限制条件下,可以得到运载火箭的最大有效载荷为218.8 kg,比之前的200 kg提高了9.4%。为了验证此条件下入轨高度的变化情况,观察图7可以得到,随着运载火箭的有效载荷增大,火箭的飞行高度随之减小,也都满足入轨高度。很明显优化后运载火箭所携带的卫星质量更大,这是在满足约束条件下的最大有效载荷。