基于多尺度内聚颗粒模型的矿石颗粒建模研究

刘钢湘，姜志宏，彭 杰

（1.中铝矿业有限公司，郑州 上街 450041；2.江西理工大学机电工程学院，江西 赣州 341000）

随着“以碎代磨”、“多碎少磨”等新工艺的提出，需对矿石的破碎原理进行深入分析。近年来，学者们不断开展对矿石破碎的机理研究，从矿石内部的细观特征来分析矿石在破碎过程中的破碎机理。Nicolas 考虑同一颗粒在多个接触之间的相互作用下的多密集颗粒材料进行模拟，分析接触力在三维空间上的分布[1]。K.Duan 等通过构建岩石颗粒模型并对其进行数值仿真，从细观力学角度来研究岩石的破碎特性及机理[2]。借助计算机数值模拟技术可以研究各向异性材料压缩试验的边界影响和矿石材料各向异性的演化规律[3-5]。Fei Wu 等通过计算机模拟技术模拟岩石蠕变实验，研究结果得到了广泛的应用[6]。李臣等利用离散元法对非规则矿石颗粒模型进行建模，并对其进行破碎仿真模拟，进而分析矿石的破碎过程及破碎能耗特性[7]。杜欣等通过X 射线断层扫描技术，并基于二值化处理和边缘点探测实现了对不规则矿石颗粒三维离散元建模[8]。蔡改贫等通过定义单元体之间不同强度特性的黏结键和不同尺度特性的单元体来构建多尺度内聚颗粒模型并对其进行挤压破碎，分析矿石的微观、细观力学特性与内部裂纹萌生、扩展情况[9]。Christian 等人给出变化的配位数方案，模拟试样在单轴压缩下的破坏过程[10]。StefLommen 等人通过体积压缩试验、渗透试验、休止角试验的数值模拟研究颗粒材料体积变化与刚度之间的关系[11]。Xiao-Ping Zhang 等人通过模拟巴西测试实验及标准岩石单轴压缩实验，对不同实验条件下的加载速率进行寻优。Kenneth C 等人运用图像分割技术获取颗粒形状，并构建与颗粒形状相似的颗粒模型。

综上所述，对于不同种类矿石颗粒模型的构建方法以及矿石的破碎过程进行大量的研究，但大多是基于宏观尺度的，没有充分考虑到矿石内部真实的几何多尺度特征，也未考虑到矿石内部在破碎过程中粘结强度的问题，从而导致矿石破碎模拟与实际破碎存在一定差异性。本文采用离散元法构建符合矿石内部真实特性的颗粒模型，为研究矿石的过程提供一种有效的建模方法。

1 矿石的几何多尺度特征分析

为了建立与实际相符合的矿石颗粒模型，需对矿石内部结构进行分析，在100 倍显微镜下观察钨矿石的内部特征，如图1所示。

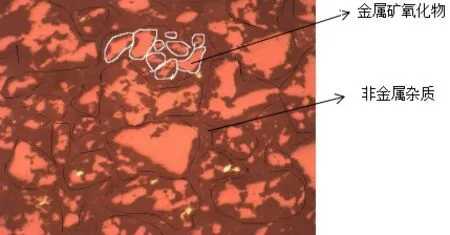
图1 矿石内部特征

由图1 可知，矿石内部由大量的金属矿氧化物以及非金属杂质组成，金属矿氧化物呈现杂乱无章的排列，即呈现非均匀分布，大小也各不相同，各金属矿氧化物之间通过非金属杂质进行粘结。因此，可将多尺度内聚颗粒模型定义为：原矿石颗粒为一级颗粒，矿石内部的金属矿氧化物为二级颗粒，即矿石大颗粒是由二级颗粒形成的聚合物；二级颗粒是由三级颗粒形成的聚合物。矿石多尺度特征实现过程如图2 所示。

图2 多尺度特征实现过程

由图2 可知，将矿石整体看作一级颗粒，当矿石受到外载荷挤压作用时，首先由图2(a)所示的矿石一级颗粒破碎成图2(b)所示的二级颗粒簇模型，当二级颗粒簇模型中的某个二级颗粒达到极限应力时，颗粒之间的粘结作用将不存在，二级颗粒破碎成三级颗粒，由于粘结作用的消失导致颗粒内部形成微裂纹，大量微裂纹的产生导致矿石进行破碎。

2 颗粒粘结本构模型

矿石颗粒是由大量细观颗粒和内部孔隙构成，颗粒之间由于存在胶结物质的作用进而将颗粒粘结成一整体，如图3 所示。颗粒粘结模型（Bonded Particle Model-BPM）能够很好地反映颗粒之间的胶结物质，因此通过粘结键的生成和断裂来实现矿石颗粒的破碎过程，粘结键如图4 所示。

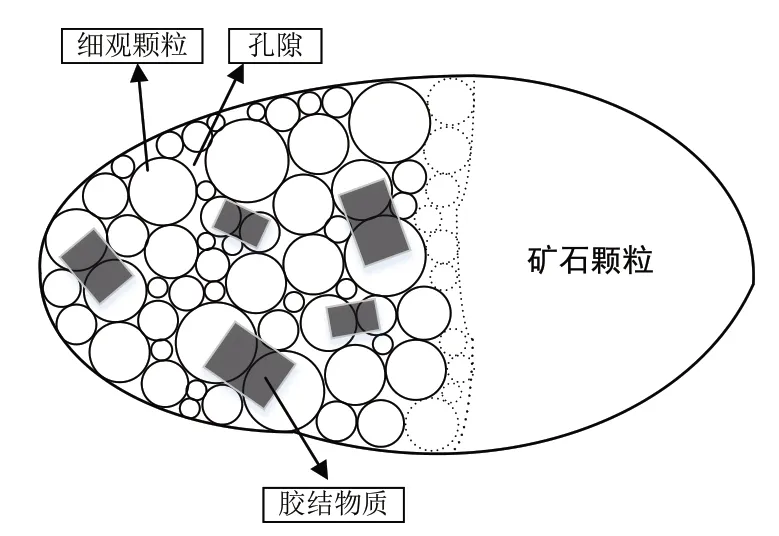
图3 矿石内部组成示意图

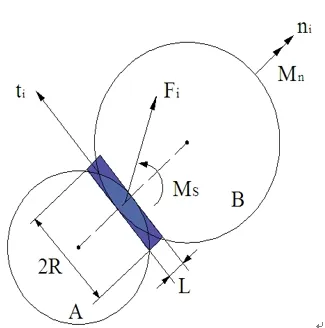
图4 粘结键示意图

粘结键所承载的总力 Fi和和总力矩Mi分别表示为：

式中，nF 为粘结力法向分量，(N)；sF 为粘结力切向分量，(N)。

ni为单位法向矢量；ti为单位切向矢量。

Mi为粘结法向力矩，(N·m)；Ms为粘结切向力矩，(N·m)。

在颗粒粘结模型中，当粘结键的法向力和切向力大于某一定值时，粘结键发生断裂，则该定值为粘结键的最大法向力σmax和最大切向力 τmax，粘结键的法向力 σn和切向力 τs可通过式(2)计算：

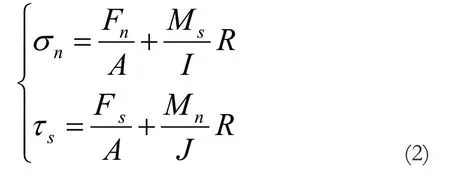
式中，A 为粘结键横截面面积，A =πR2(m2)。

R 为粘结半径，(m)。

当σn>σmax或τs>τmax时，粘结键发生断裂。

3 岩石单轴压缩破碎实验

为获取矿石的力学参数（抗压强度、弹性模量、泊松比），采用型号为PMT-150C 的力学实验系统对3 组标准岩样（mm）进行单轴压缩破碎实验，加载速度为0.002mm/s，如图5、图6 所示。

图5 PMT-150C 的力学实验系统

图6 标准岩样

通过对上述实验结果进行分析，如表1 所示。对3 组矿石岩样各应变下的应力取平均值，得其应力-应变曲线，如图7 所示。

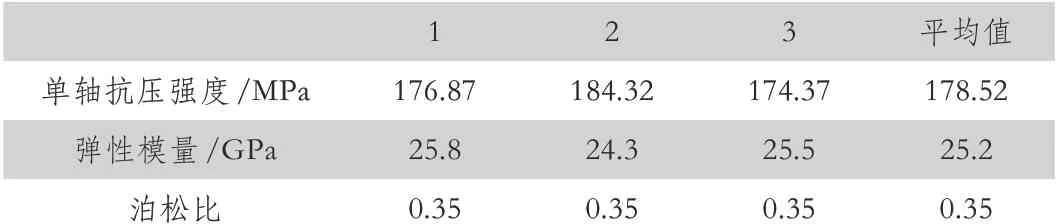
表1 岩样力学参数

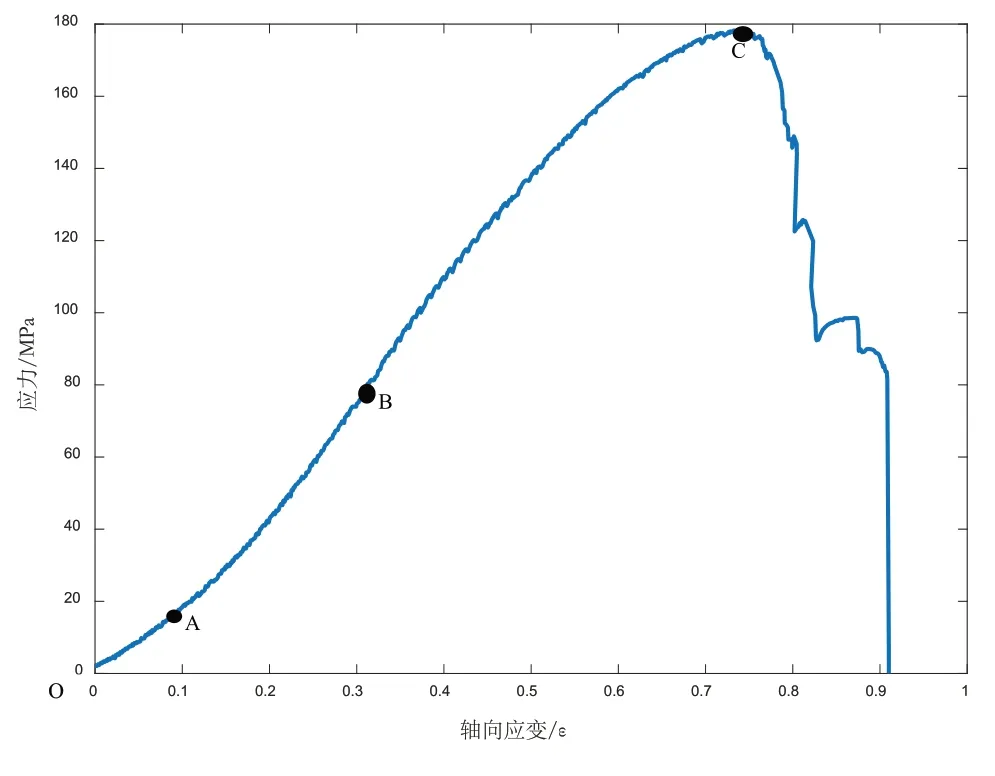
图7 标准岩样的应力-应变曲线图

采取传统的划分方式可将图7 分为：压密阶段（OA）、弹性阶段（AB）、裂纹扩展阶段（BC）和破坏阶段（C 点以后）四个阶段，各阶段的具体划分为：压密阶段应力值为峰值应力的10%；弹性阶段临界应力值为峰值应力的30%～50%。

加密阶段：曲线呈现凹形，岩石内部缺陷裂纹进行闭合，致使岩石孔隙率降低。弹性阶段：曲线呈准直线，应力与应变呈线性相关，变形是可恢复的，即撤销外部载荷可以恢复原来的状态。裂纹扩展阶段：随着外载荷的增大，岩石内部裂纹不断产生并进行扩展。破坏阶段：外载荷增加至岩石所能承受的极限时，岩石内部的裂纹发生聚集形成宏观破碎，岩石所受的弹性势能瞬间释放，岩石的应力大幅度降低。在破坏阶段之前，应力呈现逐渐增大的趋势，说明岩样没有发生塑性变形，属于脆性硬岩。

4 颗粒粘结力学参数的求解

颗粒粘结模型力学参数主要由粘结键法向刚度和切向刚度、粘结键法向强度和切向强度、粘结半径构成。其求解如式(3)所示。

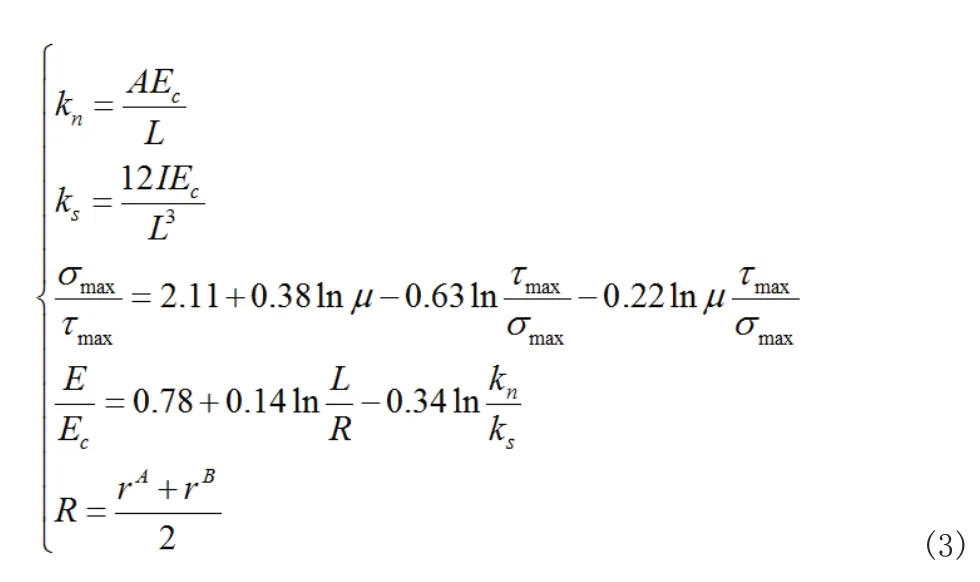
式中，A 为粘结键横截面的面积，(m2)。

Ec为弹性模量，(GPa)。

L 为粘结键长度，(m)。

I 为粘结键截面的惯性矩，(m4)。

µ 为球单元间的摩擦系数。

E 为杨氏模量，(MPa)。

R 为粘结键半径，(m)。

假设二级颗粒 rA= rB=3mm，结合单轴压缩破碎实验所获取的矿石力学参数以及矿石的固有属性，利用式(5)求解出颗粒间粘结键的粘结参数，如表2 所示。

表2 粘结键参数

5 矿石颗粒模型的建立

为建立符合实际的矿石颗粒模型，采用三维实体建模建立与实际矿石形状相似的三维几何曲面模型，将矿石几何曲面模型导入离散元软件EDEM 中，并基于表1、表2 所确定的参数建立与实际矿石相符合的颗粒模型，如图8 所示。通过EDEM 软件构建的矿石颗粒模型，既符合矿石的几何外形特征，又符合矿石的力学特性。

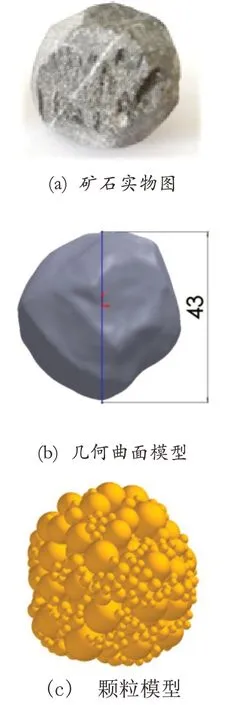
图8 矿石颗粒模型的生成

6 结论

（1）对矿石内部特征进行分析，采用多尺度内聚颗粒模型描述矿石内部特征，并通矿石单轴压缩试验获得矿石颗粒模型的相关参数。

（2）钨矿石单轴抗压强度约为178.52MPa，弹性模量约为25.2GPa，泊松比为0.35。矿石历经压密、弹性、裂纹扩展和破坏四个阶段。