双履带式巡检机器人翻越圆管能力分析

邹树梁 ，刘昌福 1，，王湘江 1，，张 德 1，

（1.南华大学机械工程学院，湖南 衡阳 421001；2.核设施应急安全作业技术与装备湖南省重点实验室，湖南 衡阳 421001）

1 引言

移动机器人在许多危险领域可以代替人类作业，极大的减少了危险源对工作人员带来的生命危害，因此得到了广泛的关注。由于履带式移动机器人具有较强的地面适应能力和越障能力，因此在应对恶劣环境下的应急救援、安全巡检等多重任务具有更突出的优势[1-3]。目前，国内外许多科研学者针对履带式机器人的越障性能进行了相关研究。例如，文献[4]分析了机器人跨越台阶和沟壑障碍的能力；文献[5]分析了机器人不同翻越姿态下的越障能力；文献[6]分析了履带机器人爬楼梯过程中的倾翻稳定性;文献[7]研究了机器人结构尺寸与楼梯台阶尺寸之间的关系。以上研究均主要针对斜坡、凸台、沟壑和楼梯等典型障碍进行分析，对机器人翻越圆管障碍的研究极少。在一些多管道的工厂内，为保证机器人顺利翻越圆管障碍完成巡检任务，充分了解机器人翻越圆管障碍的越障性能是及其必要的。

基于双履带式巡检机器人，重点针对某工厂的圆管障碍进行越障性能研究，充分考虑机器人翻越障碍过程中的几何约束、滑移稳定性条件以及倾翻稳定性条件，建立机器人的越障分析模型，得到了机器人翻越障碍的极限能力，并搭建实验平台，通过样机实验对越障分析模型进行了验证，为后续双履带式巡检机器人的优化设计提供理论依据。

2 机器人翻越圆管障碍过程分析

2.1 机器人翻越圆管障碍运动过程规划

分析机器人越障过程，将机器人翻越圆管障碍分为3个阶段：引导轮攀上圆管阶段：机器人接近圆管到引导轮攀上圆管；机体绕圆管翻转阶段：机器人脱离地面绕圆管翻转过程；机器人翻越着地阶段：机器人绕圆管翻转到脱离圆管着地过程。

机器人翻越圆管障碍的最大高度为各阶段所能达到的最大高度的较小值，且应保证机器人翻越过程中不发生失稳现象，为此，对越障过程的各个阶段进行一一分析。

2.2 机器人翻越圆管障碍过程的理论分析

2.2.1 引导轮攀上圆管阶段

机器人引导轮攀上圆管阶段可分为引导轮最初接触圆管障碍和机体处履带支撑两个阶段。

（1）引导轮与圆管最初接触阶段

图1 引导轮与圆管最初接触时的受力分析Fig.1 Force Analysis at Guide Wheel Contact Round Tube Obstacle Primitively

机器人在翻越圆管障碍过程中，将机器人引导轮离开地面瞬间视为攀越圆管的一个关键姿态，如图1所示。根据图示的几何关系，可知：

此姿态下机器人不发生滑移失稳的条件为：B点处的等效摩檫力与等效支撑力的比值不大于履带与圆管接触的最大比值μmax。由力和力矩平衡原理，整理可得到此状态下的稳定性条件：

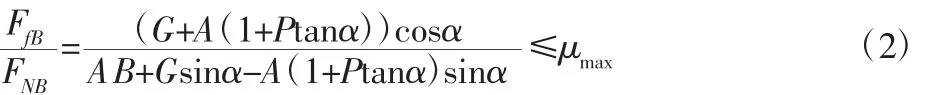
（2）机体履带支撑阶段

机器人引导轮顺利爬上圆管障碍后，进入机体履带支撑阶段，如图2所示。此状态下机器人机体处履带最高点的高度不小于圆管接触点的高度，因此，可以得到几何关系：

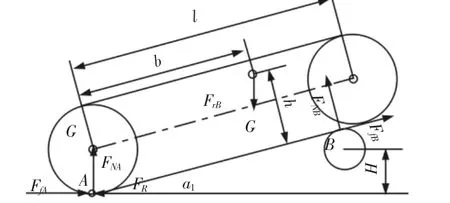
图2 机体支撑阶段受力分析Fig.2 Force Analysis at Step of Supporting in Track of Robot`Body

为使机器人能够继续前行，则需满足接触的不打滑条件：FfB/FNB≤μmax，根据图2的受力情况，由力和力矩的平衡原理，整理可得此阶段的稳定性条件：

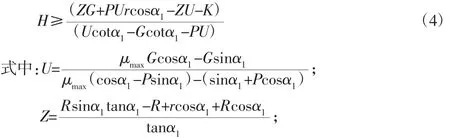
K=G［bcosα1-（h-R）sinα1］；α1—机器人的仰角。

根据重心投影法[9]，防止机器人不发生倾翻的稳定性条件是：机器人重心投影处于机器人与地面和圆管接触点之间的位置，因此可得：

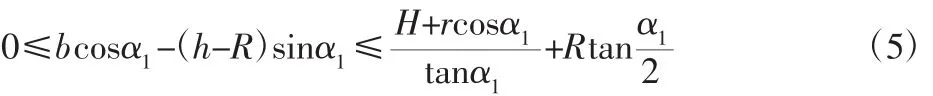
2.2.2 机体绕圆管翻转阶段

机器人引导轮攀上圆管障碍后继续前行，到达可翻转的临界状态，即：机器人重心与履带-圆管接触点处于同一竖直线，机器人恰好脱离地面，如图3所示。将机器人临界姿态作为机体绕圆管翻转阶段的关键姿态进行分析。

图3 机器人发生翻转的临界状态Fig.3 Critical State of Robot Flipping

根据图3的几何关系，针对不同半径的圆管障碍，圆管高度与机器人仰角关系如下：

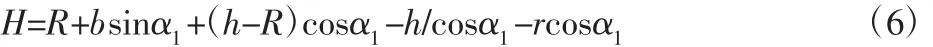
式中：H—圆管轴心离地高度；r—圆管半径；α1—机器人仰角；同理，机器人在临界状态下不打滑条件为：FfB/FNB≤μmax，根据图4的受力分析，整理可得此阶段的不打滑条件：

随着机器人仰角的不断增加，机器人会出现向后倾翻的想象，为防止机器人此阶段向后倾翻，则需满足倾翻稳定性条件：

2.2.3 机器人翻越圆管着地阶段

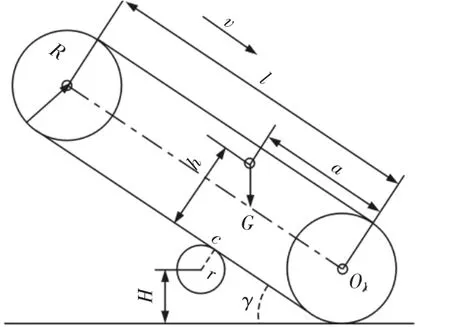
图4 机器人引导轮着地阶段受力分析Fig.4 Force Analysis at Step of Guide Wheel Touch the Ground

机器人在着地阶段过程中，最可能发生失稳现象是在机器人翻转着地前的瞬间，因此，确定机器人翻转着地瞬间为此阶段的关键姿态，如图4所示。根据图4所示，此时机器人机体处履带最高点高度不应小于与圆管的接触点高度。因此，可以得到此姿态下，机器人应满足几何条件

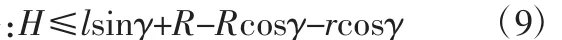
式中：H—圆管轴心到地面的高度；r—圆管半径；γ—机器人着地时的俯角。

机器人引导轮着地前的瞬间同样满足履带接触不打滑条件：FfB/FNB≤μmax，整理可得

同理可根据重心投影法[9]，得到机器人着地时的倾翻稳定性约束为：

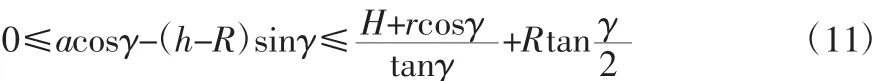
机器人最终能顺利翻越圆管的最大高度为各个阶段下机器人能达到高度的较小值：

3 翻越圆管障碍过程的仿真分析

3.1 双履带式巡检机器人结构介绍

主要基于自制的双履带式巡检机器人样机进行分析，机器人主要由机体、履带、引导轮、驱动轮、支重轮等组成，其基本参数，如表1所示。

针对某工厂内的圆管障碍进行考察，选取直径D=60mm的钢管为圆管障碍，根据履带棱与圆管的接触交互力分析[6]，计算可得履带与圆管接触的等效摩檫力与等效支撑力的最大比值μmax=1.61。

表1 机器人主要参数Tab.1 The Main Parameters of Robot

3.2 机器人翻越圆管过程仿真分析

3.2.1 引导轮与圆管最初接触阶段

根据式（2）可以得出机器人此姿态下不发生滑移的稳定性条件为：引导轮偏转角最小不小于αmin=12°；由图5可知：越障高度H随着偏转角α的增大而减小，因此可得，此阶段机器人能适应的最大高度在αmin=12°处取得：Hmax1=89.5mm，如图5所示。

图5 引导轮与圆管最初接触阶段Fig.5 Step at Guide Wheel Contact Round Tube Obstacle Primitively

3.2.2 引导轮攀上圆管机体支撑阶段

机器人处于机体支撑阶段时，不发生失稳的可行性区域阴影部分，此阶段机器人能适应的最大高度在机器人不发生倾翻的最大仰角处取得，Hmax2=477mm，如图6所示。

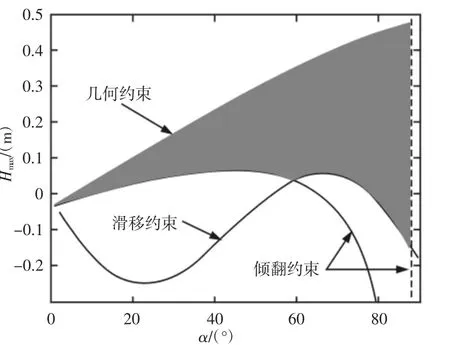
图6 机体支撑阶段Fig.6 Step of Supporting in Track of Robot’Body

3.2.3 机体绕圆管翻转阶段

由图7可知：当圆管直径为D=60mm，机器人能翻越圆管离地面的最大高度Hmax2=66mm，此时，机器人仰角α=45°。因此，机器人能绕圆管发生翻转的最大高度为Hmax3=66mm，如图7所示。

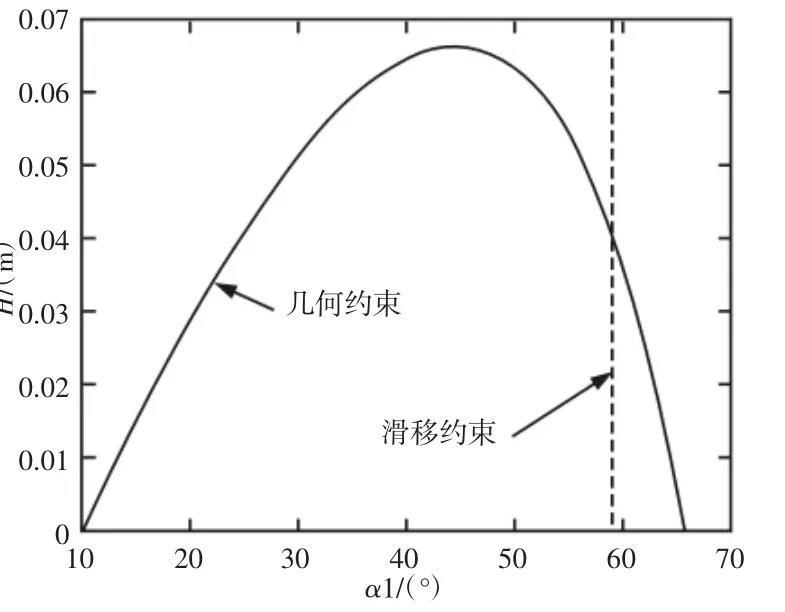
图7 机器人发生翻转的临界状态Fig.7 Critical State of Robot Flipping

3.2.4 机器人翻越圆管着地阶段

机器人在着地阶段不发生失稳的可行高度在阴影部分，因此，机器人在此阶段越障的最大高度值在不发生滑移的最大俯角γmax=58°时取得：Hmax4=341.5mm，如图 8所示。

图8 机器人翻越圆管着地阶段Fig.8 Step of Robot Touch the Ground After Climbing the Round Tube Obstacle

综上所述，根据式（12）可以得到机器人能翻越直径D=60mm的钢制圆管障碍的最大高度为：Hmax=66mm。

4 翻越圆管过程的实验分析

为了进一步验证双履带式巡检机器人样机的越障性能，选取直径D=60的钢制圆管，搭建实验平台进行了样机实验，最终得到了各阶段的最大理论高度和实验高度，如表2所示。最终确定机器人能翻越直径D=60mm的钢制圆管障碍的最大可行高度为：Hmax=70mm。

表2 各阶段的最大理论高度和实验高度Tab.2 The Maximum Theoretical Height and the Experimental Height of Each Stage

5 结论

（1）规划了双履带式巡检机器人翻越圆管障碍的过程，确定了翻越过程中各阶段的关键姿态；视机器人翻越过程为准静态过程，从越障过程的几何关系、不发生滑移和不发生倾翻的稳定性条件进行分析，建立了双履带式巡检机器人翻越圆管障碍过程中各个阶段下的越障能力的理论分析模型，为机器人翻越圆管障碍提供可行的理论分析依据。（2）对双履带式巡检机器人翻越圆管障碍进行仿真分析和实验研究，得到了机器人能顺利翻越直径D=60mm的钢制圆管的最大高度Hmax=70mm，进一步验证了越障理论模型的可行性。