磁吸附轮式擦窗机器人动力学建模与仿真
2020-03-28孙立新李峰亮王小旭
孙立新,李峰亮,董 鹏,王小旭
(河北工业大学机械工程学院,天津 300131)
1 引言
随着社会的进步与发展,城市土地占用率越来越高,高层建筑越来越多,由此带来一系列关于高层建筑玻璃清洗问题。国内专家对于擦窗机器人领域已经进行深入的研究。对于应用于擦拭玻璃窗的擦窗清洁机器人来讲,既需要考虑其功能的实现,同时还需要考虑运动性能。擦窗机器人的效率、擦拭清洁度、噪音大小和智能化程度等是其功能特征指标;磁吸附能力、驱动轮打滑程度、行走速度等等是其运动功能特性。
目前已知擦窗机器人基本是采用磁铁、真空、负压式等吸附方式。而磁吸附式以其结构简单,市场易得得到较多的应用。
擦玻璃机器人与地面移动机器人的不同点在于:(1)擦窗机器人需要获得合适的磁吸附力和驱动扭矩,保证其在玻璃表面匀速运动,不发生打滑和倾覆。(2)清洁装置需要合适的摩擦力以保证对玻璃表面的擦拭效果。清洁装置所需摩擦力是有利摩擦力,而有利摩擦力与机器人移动所需驱动扭矩是一对矛盾,因此研究二者关系将是擦窗机器人力学分析的新方向。同时磁吸附力增大或者清洁装置摩擦系数增大,会对驱动轮扭矩造成影响,在此也应该要分析轮子不同程度打滑情况下,对扭矩和驱动轮摩擦系数的影响,用以选择合适的扭矩和驱动轮摩擦系数,保证机器人整体功能的实现。
对WCWR进行分析,研究其在玻璃平面匀速运动所需最小磁力,并且仿真分析。并在建立机器人轮系动力学模型基础上,研究磁吸附力和运动性能、清洁装置有利摩擦力、打滑程度和驱动扭矩间的关系。
2 WCWR匀速运动状态下静力学分析
机器人在玻璃表面的匀速运动是垂直方向时,则驱动轮和玻璃表面的摩擦力既是其移动的驱动力。假设WCWR匀速移动,其受力分析,如图1所示。

图1 WCWR匀速运动状态静力学分析Fig.1 Static Analysis of WCWR Uniform Motion State
图中:{c0,x0,y0,z0}—固定坐标系;{c1,x1,y1,z1}—模型坐标系;主动面重心;O1,O2—两驱动轮中心;O3—从动面重心;2b—机器人轮间距;:机器人航向角;G—机器人总重力;G1—主动面重力;G2—从动面重力;f0—玻璃和清洁装置间的动摩擦力;f1/f2—玻璃和单个前/后轮的动摩擦力;fc—单个磁铁吸附力;N0—玻璃平面对主动面支持力;N1—玻璃平面对上驱动轮支持力;N2—玻璃平面对下驱动轮支持力;N3—玻璃平面对从动面总支持力;L—玻璃厚度;d—磁铁质心到两轮中心距离;LC—磁铁质心到玻璃平面高度;h1/h2—主/从动面质心到玻璃平面距离。
由上图分析可得知,WCWR在垂直玻璃平面匀速运动时,摩擦力时刻发生改变,其中清洁装置摩擦力和机器人运动方向相反,属于滚动摩擦,阻碍机器人移动,驱动轮与玻璃平面存在动摩擦。可由上图侧视图分析出轮系受力方程如下:

式中:f0=μ0N0;f1=μ1N1;f2=μ2N2;μ0—清洁装置与玻璃表面滑动摩擦系数;μ1—驱动轮与玻璃表面动摩擦系数。
WCWR在玻璃表面能够匀速运动时,其应该满足以下两个方面:1,不下滑:2,正向和侧向不发生倾覆。则既有公式如下:

WCWR受磁吸附力贴附在玻璃表面时,驱动轮和擦拭装置应变相同,应力不同,设作用于清洁装置和驱动轮上的压力之比是α,且力在清洁装置上均匀分布,则可根据胡克定律得到磁吸附力分别是:

式中:FW—驱动轮所受磁力;FC—总磁力;E0,E1—清洁装置和驱动轮的弹性模量;A0,A1—清洁装置和驱动轮与玻璃接触有效面积。则:α=(FC-FW)/FW=E0A0/E1A1,且有FC=f1+f2=μ1(N1+N2),
由上分析可知,满足WCWR安全吸附在在玻璃表面做匀速运动时的最小单个磁铁磁力fc:

3 擦窗机器人WCWR磁吸附模型
由上式(4)分析可知,影响磁吸附式擦窗机器人的最小磁力的主要因素有:清洁装置和驱动轮对玻璃表面的摩擦系数,清洁装置和驱动轮与玻璃表面的有效接触面积,机器人的尺寸和移动位姿等等。
由于摩擦系数在不同工况会受影响,为了简化分析,在此处将接触视为刚性接触,同时忽略摩擦副之间的变形,按照普通情况则有:μ0<μ1<1,由式(4)则可归结为WCWR的磁吸附力模型:

在此取μ0=0.2,μ1=0.6,同时代入WCWR的其他设计参数,可由式(4)得出磁吸附力和机器人航向角之间的关系,如图2所示。

图2 单个磁铁吸力与航向角关系曲线Fig.2 Single Magnet Suction and Heading Angle Curve
3 单个驱动轮动力学方程
根据车辆动力学理论,车轮式移动机器人运动的牵引力是由于车轮与地面接触发生变形产生附着力。轮胎只要与玻璃壁面接触,轮子就会承受到切向力,车轮就会发生打滑现象。
一般滚动都是在假设驱动轮没有发生侧向或横向滑动的条件之下建立的,同时要求其运动速度不是很高,又或者功率/轮负荷较小的状况下才能成立。而WCWR则需要在垂直或倾斜的玻璃墙面上运动,轮子的负荷压力则由磁力直接提供,磁吸附力的增加将引起玻璃表面的运动阻力(包括清洁装置阻力和驱动轮滚动阻力)和驱动功率的增加,磁力减小易造成驱动力不足,引起或加剧驱动轮的打滑现象,会造成控制系统的不可控或系统工作的不稳定性。
驱动系统提供的驱动力较大于磁铁提供的磁吸附力时,驱动轮就易出现打滑现象。而且玻璃表面存在的水渍或者尘土粘附在驱动轮时,也容易造成WCWR的打滑。此外,WCWR在行走过程中姿态的不断变化,由自身重力产生的侧作用力作用于驱动轮,从而造成驱动轮横向或侧向的滑移也是造成打滑的重要原因。
因此,纯理想滚动条件并不符合实际情况。在此假设条件下,设υw是车轮中心速度ωw是车轮角速度,并且满足:

在此我们引入滑转率s,以此来表示车轮打滑的程度,且滑转率可表示为:

式中:ω*=υw/r;ω=max{ωw,ω*}。S=-1,0,1—完全抱死拖滑、纯理想滚动以及原地打滑三种车轮状态;若只考虑在驱动情况下,则0 图3 单个驱动轮受力分析Fig.3 Single Drive Wheel Force Analysis 图中:m1和J1—前轮轮子质量与惯性矩;T1—驱动力矩;FS—作用于轴的反作用力,并且 FS=(1/2)f0;式中:Mf1—滚动阻力偶,并且 Mf1=δN1,式中 δ=e/r,δ—滚动阻力系数,N1—玻璃面对轮子支持力,且N1=f1/nw,式中:nw—承压系数;f1—玻璃表面摩擦力,既是轮子与玻璃面压缩产生的切向力,跟车轮动摩擦系数μ1和N1有关。 我们假设用以下分段直线代替曲线μ1-s关系曲线[6],即: 当s从零开始上升时,μ1随s线性增加,之后μ1增加减慢,达到最大值 μh后,s增加而 μ1一直下降到 μg。在 μh~μg段,驱动轮急剧打滑,机器人处于极不稳定的运动状态。 由图3前轮受力分析可得: 当ω˙=0时,驱动轮匀速运动、机器人平稳运行,以前、后驱动轮做研究对象,以各自轮心为矩心,则有: 将式中(9)中两式相加,得到: 将式(1)代入式(10)中,化简可得单个驱动轮扭矩: 将式(7)代入式(11)得: 由式(11)可以看出,WCWR驱动轮的扭矩主要受车轮半径、磁铁吸附力、驱动轮滑转率、清洁装置与玻璃表面摩擦系数、机器人航向角度等因素的影响,在以上因素中,清洁装置与玻璃表面摩擦力会阻碍机器人的运动,但是较大的摩擦系数μ0有利于擦拭玻璃平面,达到清洁效果,所以我们在考虑驱动轮输出扭矩时,应以尽可能大的μ0作为清洁器机器人的设计指标。在此,为了研究WCWR在打滑程度不同的情况下,驱动轮扭矩和机器人航向角之间的关系,以此来选取合适的驱动轮与玻璃表面的摩擦系数和驱动扭矩,用以保证WCWR的稳定行驶。在此以驱动轮扭矩模型中的作为自变量,驱动扭矩当做因变量,同时代入智能擦窗机器人其他设计参数,对驱动轮驱动扭矩进行仿真分析,其结果,如图4所示。 图4 驱动扭矩与航向角、滑转率关系曲线Fig.4 Drive Torque and Heading Angle,Slip Rate Curve 由仿真可知:机器人在航向角度θ=90时,所需驱动扭矩最大,在s取值0 擦窗机器人样机研发中测得参数:G=15N,b=0.12M,由驱动轮材料选取与玻璃表面之间的摩擦系数μ1=0.6,根据机器人擦拭方式选取μ0=0.2,磁铁选取排号N52,直径20mm,厚度12mm,选取DC24V直流电机,输出扭矩T=15N·m,机器人放在玻璃厚度L=0.1m上进行实验。由仿真分析可知,机器人在航向角θ=90时所需最小磁力和输出扭矩最大,应此实验在该基础条件下进行。同时受到实验室条件的限制,在此我采用一种较为简单且常用的检测方法,即使用万能表检测机器在运行过程中电流和电压的变化,以此来判断机器运行过程中是否出现打滑现象的发生。若机器平稳运行则机器的电流或者电压不会出现突变,以此标准作为判断依据。实验结果显示,机器人能够在该参数下平稳匀速运动。电流或者电压突变较少,原因是由于主动面玻璃和驱动轮表面清洁程度较差时,就会伴随一些打滑现象发生,此现象则有待于进一步研究。 图5 样机实验现场Fig.5 Prototype Experimental Site 对磁吸附式擦窗机器人(WCWR)进行动力学建模仿真,同时引入车辆动力学,对驱动力进行受力分析,分析其在不同程度打滑情况下,驱动扭矩与滑转率的关系。由仿真分析可知,机器人正常行走的主要因素与磁吸附力、清洁装置摩擦系数和驱动扭矩等。 通过仿真我们可以选择合适的磁吸附力,在尽可能选择大的清洁摩擦系数以保证擦拭效果的前提下,调整合适的驱动轮扭矩和驱动轮与玻璃表面的摩擦系数,以保证机器人在玻璃表面平稳匀速行走,削弱打滑对运动轨迹的影响同时达到对玻璃表面的清洗。对磁吸附式擦窗机器人的设计提供了方法,同时对擦窗机器在打滑情况下的运动控制和擦窗效果提供了理论基础,为WCWR能在玻璃表面正常行走提供了新的研究思路。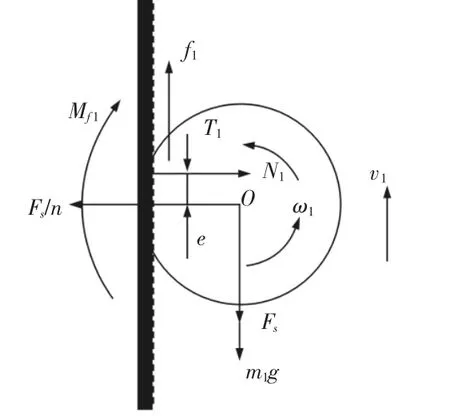






5 样机实验测试

6 结语
