直接有限环的若干扩张

马广琳， 王 尧， 任艳丽

(1.南京信息工程大学 数学与统计学院，江苏 南京 210044；2.南京晓庄学院 信息工程学院，江苏 南京 211171)

本文假定所研究的环R都是有单位元1的结合环(除非另有说明)。称环R为直接有限环[1](也称为直有限环或戴德金有限环)，若对任意的a,b∈R,当ab=1时，则有ba=1。交换环显然是直接有限环。称环R为稳定有限环[2]，若R上的全体各级全矩阵环都是直接有限环。有关直接有限环的最早研究参见文献[3-5]。称环R为对称环[6]，若对任意的a,b,c∈R，由abc=0可以推出acb=0。称环R为可逆环[7]，若对任意的a,b∈R，由ab=0可以推出ba=0。称环R为半交换环[8]，若对任意的a,b∈R，由ab=0可以推出aRb=0。称环R为2-素环，若R中幂零元素集合与素根相等。由文献[9，定理1.3]，约化环(即环没有非零的幂零元)是对称环，对称环显然是可逆环。由文献[6，命题1.3]，可逆环是半交换环，但这些推导是不可逆的(参见文献[9，10])。并且，若环中没有单位元1，则对称环未必是可逆环[11]。由文献[8]，半交换环是2-素环，2-素环又是直接有限环[12]。因此约化环、对称环、可逆环、半交换环都是直接有限环。近年来，文献[13，14]研究了直接有限环的一些刻画和其与相关环的关系。本文主要讨论直接有限环的一些扩张性质，如理想扩张、Dorroh扩张、Nagata扩张、Jordon扩张等。

1 直接有限环的扩张

命题1.1设R是直接有限环，则R的含单位元1的子环也是直接有限环。

(1)R的子环是直接有限环；

(2)R的同态像是直接有限环。

命题1.2设{Rγ|γ∈Γ}是一族环，则R=Πγ∈ΓRγ是直接有限环当且仅当每个Rγ是直接有限环。

证明设R是直接有限环，aγ,bγ∈Rγ满足aγbγ=1，则有α=(aγ)γ∈Γ，β=(bγ)γ∈Γ∈R使得αβ=(1γ)γ∈Γ。因为R是直接有限环，所以βα=(1γ)γ∈Γ，从而对任意的γ∈Γ，bγaγ=1，这推出每个Rγ是直接有限环。

反之，设每个Rγ是直接有限环，α=(aγ)γ∈Γ，β=(bγ)γ∈Γ∈R满足αβ=(1γ)γ∈Γ，则

对任意的γ∈Γ，aγbγ=1。因为Rγ是直接有限环，所以bγaγ=1，故βα=(1γ)γ∈Γ，这推出R是直接有限环。

设D是一个环，C是D的子环且1D∈C，令

R[D,C]={(d1,…,dn,c,c…)|di∈D,c∈C,n≥1}

R{D,C}={(d1,…,dn,cn+1,cn+2,…)|di∈D,cj∈C,n≥1}

在R{D,C}上按对应分量定义加法和乘法，则R{D,C}作成一个有单位元的环。显然R[D,C]是R{D,C}的一个子环。

命题1.3R{D,C}是直接有限环当且仅当D是直接有限环。

设R是一个环，R[[x]]表示R上的形式幂级数环。设α是环R上的一个非零自同态。R[[x;a]]的元素形式和加法运算与形式幂级数环R[[x]]一致，乘法运算定义为xr=α(r)x,r∈R，则R[[x;a]]按上述运算构成一个环，称为斜幂级数环。

定理1.1设R是环，α是R上的一个自同态且α(1)=1，则R[[x;α]]是直接有限环当且仅当R是直接有限环。

证明必要性是显然的，下证充分性。

设R是直接有限环，f(x),g(x)∈R[[x;α]]，满足f(x)g(x)=1，令

f(x)=a0+a1x+a2x…,g(x)=b0+b1x+b2x2+…,

则

a0b0=1

(1)

a0b1+a1α(b0)=0

(2)

a0b2+a1α(b1)+a2α2(b0)=0

(3)

a0b3+a1α(b2)+a2α2(b1)+a3α3(b0)=0

(4)

…………

因为R是直接有限环，所以b0a0=1。由(2)式得b1=-b0a1α(b0)，a1=-a0b1α(a0)。由b0×(2)×α(a0)得b0a1+b1α(a0)=0。由(3)式得b2=-b0(a1α(b1)+a2α2(b0))。将b1代入b0×(3)×α2(a0)得b0a2+b1α(a1)+b2α2(a0)=0。再将b1,a1,b2代入b0×(4)×α3(a0)得b0a3+b1α(a2)+b2α2(a1)+b3α3(a0)=0，如此继续下去，可得g(x)f(x)=1，这推出R[[x;α]]是直接有限环。

推论1.1R[[x]]是直接有限环当且仅当R是直接有限环。

设R是一个环，α是环R上的一个自同态，n是正整数，Nasr-Isfahani在文献[15]中定义斜三角矩阵环为

其中加法为矩阵的加法，乘法定义为：

其中ci=a0α0(bi)+a1α1(bi-1)+…+aiαi(b0)，0≤i≤n-1。可将Tn(R,α)的元素表示为(a0,a1,…,an-1)，且存在环同构φ：R[x;α]/(xn)→Tn(R,α)，φ(a0+a1x+…an-1xn-1+(xn))=(a0,a1,…,an-1),ai∈R,0≤i≤n-1，因此Tn(R,α)≅R[x;α]/(xn)。

推论1.2设R是环，α是R上的一个自同态且α(1)=1，则Tn(R,α)是直接有限环当且仅当R是直接有限环。

推论1.3设R是环，α是R上的一个自同态且α(1)=1，则环R[x;α]/(xn)是直接有限环当且仅当R是直接有限环。

定理1.2环T(R,M)是直接有限环当且仅当R是直接有限环。

证明设R是直接有限环，(a1,m1),(a2,m2)∈T(R,M)，满足(a1,m1)(a2,m2)=(1,0)，则有

a1a2=1

(1)

a1m2+m1a2=0

(2)

依假设得a2a1=1。由a2×(2)×a1可得m2a1+a2m1=0，从而

(a2,m2)(a1,m1)=(a2a1,a2m1+m2a1)=(1,0)，

这推出T(R,M)是直接有限环。

反之，T(R,M)是直接有限环，a1,a2∈R满足a1a2=1，则有(a1,0),(a2,0)∈T(R,M)且(a1,0)(a2,0)=(1,0)，从而(a2,0)(a1,0)=(1,0)，故a2a1=1，这推出R也是直接有限环。

设R是一个环，V是一个(R,R)-双模，且V是一个一般环(未必有单位元1)，满足(vw)r=v(wr)，(vr)w=v(rw)和(rv)w=r(vw)，对所有的v,w∈V和r∈R。称环I(R;V)=R⊕V为R通过V的理想扩张，其中加法为通常加法，乘法满足(r,v)(s,w)=(rs,rw+vs+vw)。

定理1.3设S=I(R;V)是R通过V的理想扩张，若R是直接有限环且V2=0，则S是直接有限环。

证明设R是直接有限环且V2=0，(r1,v1),(r2,v2)∈D满足(r1,v1)(r2,v2)=(1,0)，则有

r1r2=1

(1)

r1v2+v1r2+v1v2=0

(2)

依假设得r2r1=1，且

r1v2+v1r2=0

(3)

由r2×(3)×r1可得v2r1+r2v1=0，从而

(r2,v2)(r1,v1)=(r2r1,r2v1+v2r1+v2v1)=(r2r1,r2v1+v2r1)=(1,0)，

这推出S是直接有限环。

设环R(未必有单位元1)是交换环S上的代数，称环R×S是R通过S的Dorroh扩张，其加法为对应分量相加，乘法为(r1,s1)(r2,s2)=(r1r2+s1r2+s2r1,s1s2)，其中ri∈R，si∈S。特别地，当Dorroh扩张中的交换环S是整数环Z时，称R×Z为R的代数扩张，记为R*。

推论1.4设S是交换环，R是幂零环且是S上的代数，D是R通过S的Dorroh扩张，若R2=0，则D是直接有限环。

推论1.5设R是环，若R2=0，则R的代数扩张R*是直接有限环。

Nagata在文献[16]中，设环R是一个交换环，M是左R-模，σ是环R的一个自同态，称环R⊕M是R通过M与σ的Nagata扩张，其中加法为对应分量相加，乘法满足(r1,m1)(r2,m2)=(r1r2,σ(r1)m2+r2m1)。

定理1.4设R是一个交换环，M是左R-模，σ是环R的一个自同态，N是R通过M与σ的Nagata扩张，若σ(1)=1,则N是直接有限环。

证明设σ(1)=1，(r1,m1),(r2,m2)∈N满足(r1,m1)(r2,m2)=(1,0)，则

r1r2=1

(1)

σ(r1)m2+r2m1=0

(2)

因为R是交换环，所以r2r1=1。由r1×σ(r2)×(2)得r1σ(r2)σ(r1)m2+r1σ(r2)r2m1=0。又σ(1)=1，从而有r1m2+σ(r2)m1=0，故(r2,m2),(r1,m1)=(r2r1,σ(r2)m1+r1m2)=(1,0)，因此N是直接有限环。

定理1.5设R是环，α是R上的一个单同态，A是R的Jordan扩张，若α(1)=1，则A是直接有限环当且仅当R是直接有限环。

证明必要性是显然的，下证充分性。

设R是直接有限环，a,b∈A满足ab=1，那么一定存在正整数n和m，使得αn(a)，αm(b)∈R。令l=m+n，则有αl(a),αl(b)∈R且αl(a)αl(b)=αl(ab)=1。因为R是直接有限环，所以αl(b)αl(a)=1又α是一个单同态且α(1)=1,故ba=1，这推出A是直接有限环。

环范畴中的一个直系统{Aα,φαβ|α,β∈I}的直极限就是一个对(A,(ηα)α∈I)，其中A是一个环，任意的α∈I,ηα:Aα→A是单同态，它们满足：

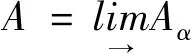
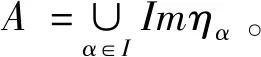
a=ηα(aα)=ηkφαk(aα)和b=ηβ(aβ)=ηkφβk(bβ)，

从而ab=ηkφαk(aα)ηkφβk(bβ)=ηk(φαk(aα)φβk(aβ))=1。又ηk是一个单同态且ηα(1Aα)=1A，那么φαk(aα)φβk(bβ)=1。因为φαk(aα),φβk(bβ)∈Ak，又Ak是直接有限环，则φβk(bβ)φαk(aα)=1，进而1=ηk(φβk(bβ)φαk(aα))=ηkφβk(bβ)ηkφαk(aα)=ηβ(bβ)ηα(aα)=ba，这推出A是直接有限环。