数理统计法与传统倍数法进行特高品位处理的比较及建议

倪 瑞，孙尚信，周翔武

（1.中陕核工业集团地质调查院有限公司，陕西 西安 710199；2.中国铝业公司矿产资源管理部资源管理处，北京 100082）

在我国地质矿产行业资源储量估算中，对于特高品位处理既有现行规范的传统倍数法，也有数理统计法，且以前者为主。对于同一矿体，二者分属于不同的理论体系，往往具有不同的界定值和处理办法，其中的争论也颇多。但二者之间有无内在联系？如何比较评判其合理性？本文从特高品位的特点入手，再通过实例进行数据分析，探讨其数理规律，并试图揭露其内在联系，最后就特高品位处理提出笔者的建议。

1 传统法处理特高品位的方法及存在不足

如何界定特高品位？我国现行规范中明确传统倍数法，指出“特高品位值一般取矿体平均品位的6倍～8倍来衡量。当矿体品位变化系数大时采用上限值，变化系数小时采用下限值”。其处理方法是“用特高品位所影响块段的平均品位”或大厚度“单工程平均品位代替”；同时允许“用SD储量计算法时，用削减值代替特高品位，置于原始数据中参与计算”。这里的SD法处理法，就是统计学方法处理法。

通过上述，笔者觉得现行规范系统虽然明确了特高品位值的界定方法和处理方法，但尚不能令人满意，主要表现在：

（1）对于特高品位的界定倍数存在不足，一是缺少理论依据，为什么是6倍～8倍？没有进一步阐明；二是《固体矿产勘查总则》中同时讲明可以用SD法界定特高品位，但对于SD法如何定义特高品位，没有统一的标准。

（2）对于特高品位的处理方法存在争议，如当用块段平均品位值代替特高值时，就造成特高值被处理后明显低于其临近值，这是不合理的。同时，准许SD法按削减值代替特高品位，而倍数法采用均值替代特高品位值，对于同一矿体而言，出现了对同一对象的双重标准问题。

2 数理统计法特处理特高品位的方法分析

随着三维软件的推广使用，数理统计法处理特高品位越来越多地被采用。常用方法有两种：一是按一定水平估值法，二是累积曲线拐点法。

水平估值法：基于满足同一正态分布的样本，每给定一个水平，就可对该水平下置信区间进行估值，从而得出特高品位估计值的方法。常见给定水平如a=5%，查标准正态分布表Za/2=Z2.5%，查得系数为1.96，特高品位估值为“均值+1.96×均方差”。采用截取法（削减值）处理，即用特高品位估值来代替大于该值的样品值参与特高品位计算。

累积曲线断点（拐点）法：通过对矿体样本品位作累积曲线图，寻找品位断点（拐点），来确定特高品位。

相对于传统法，数理统计法明确给出特高品位所对应的置信水平及置信区间，其数理意义明确。用截取法处理似乎较用均值代替更合理。

3 传统法与数理统计法对同一矿体进行特高品位处理效果对比

以实例R斑岩铜矿为例，其主矿体5688个样品统计规律如下：

表1 R斑岩铜矿样品统计

从图1和2可以看出，该矿床Cu品位基本服从正态分布，同时存在少量离散点，即存在特高品位。

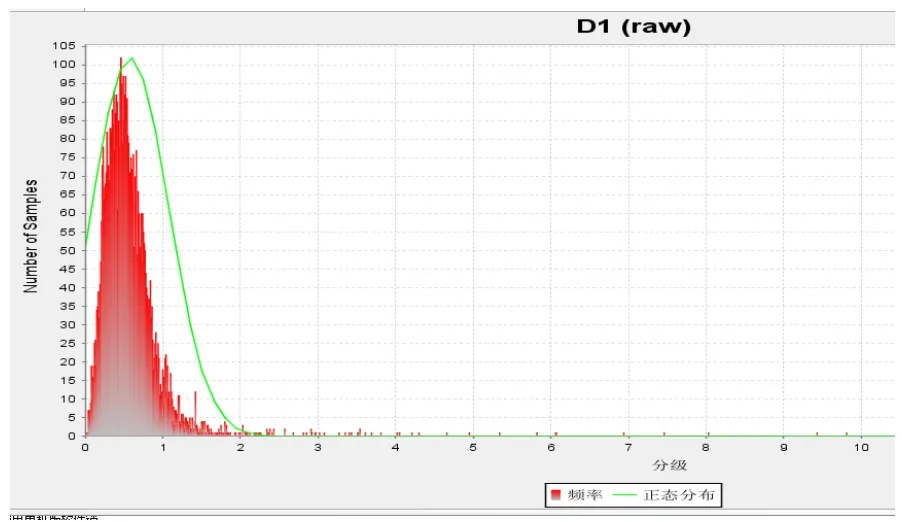
图1 SURPAC软件统计分析R斑岩铜矿矿体铜品位频率曲线

纵轴为分组频率值，横轴为铜品位分组平均值，组距0.01%。

分别按传统法和数理统计法对矿体特高品位处理如下：

3.1 传统法对矿体进行特高品位处理

R矿Cu品位均值0.5793%，品位变化系数为85.42%，介于60%～150%之间，属于较均匀类，故取均值的7倍作为特高品位下限值，即：

0.5794×7=4.06（%）

特高品位值4.06%对应频率累积99.81%位置（图2中位置2），处理数据14个。

3.2 统计法特高品位处理

方案a：水平估值法。

取水平5%，查概率Z0.05/2，对应系数1.96，故特高品位取值：

0.5793+1.96×0.4949=1.55（%）

特高品位1.55%对应频率累积曲线98.17%位置（图2中位置6），处理数据105个。

方案b：分析累积曲线拐点法。

按组距0.001%做矿体频率累积曲线图，品位频率累积频率曲线服从正态分布，且存在少量离散点（图2）。查找出5个断点，特征点分别对应图、表中的1点～5点，也就是说，按累积曲线拐点法，可以选择其中5个中的一个。一般选初始明显断点（拐点）如本例图2中较接近的点1、2或3中的一个。

表2 特征品位值一览表

采用SURPAC软件做频率累积曲线进行观察如下：

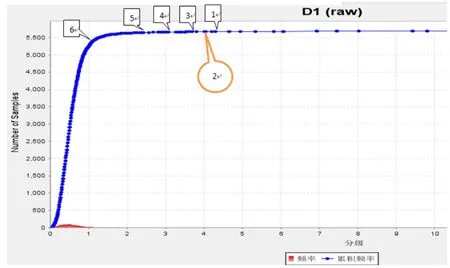
图2 SURPAC软件R斑岩铜矿矿体铜品位频率曲线累积曲线

纵轴为分组频率累积值，横轴为铜品位分组平均值，组距0.01%。

4 传统法和数理统计法之深度比较及其内在联系

可以看出，统计法方案a与传统法比较，二者差别极大，表现在传统法特高下限值4.05%是统计法方案a对应值1.55%的2.6倍；处理样品14个仅相当于统计法方案a的105件的13.3%，二者不具有相合性。即使取a=0.05%，其特征值0.5793+3.48×0.4949=2.30（%）（说明 ：3.48为函数表中最大值；如果按特高值4.05反推，应取值7，几乎是必然事件了，已经超出函数表范围），仍需要处理48个，仍然有较大差异。

统计法方案b与传统法比较，当取值靠近累积曲线末梢时，如1号～3号位置对应点，二者接近，即靠近累积曲线末梢拐点所确定的特高品位值接近于传统法，处理样品数也接近。

换句话说，传统法和统计法b方案的初始断点（拐点）值接近，传统法确定特高品位方法是合理的。

进一步讨论累积曲线影响断点初始位置的主要因素。通过作图发现，如果认为加大分组间隔即组距，观察累积曲线断点（拐点）值有明显变化（图3～图5）。

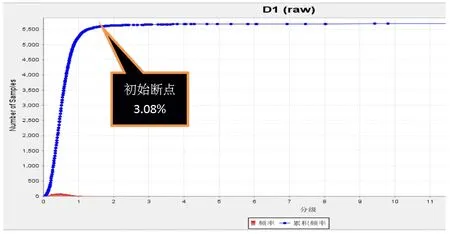
图3 组距=0.001%时频率累积曲线初始断点位置观察

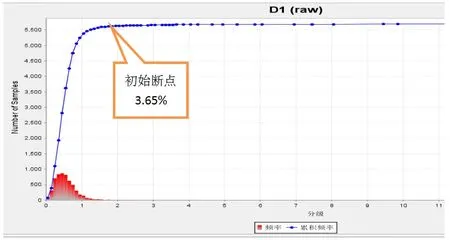
图4 组距=0.1%时频率累积曲线初始断点位置观察

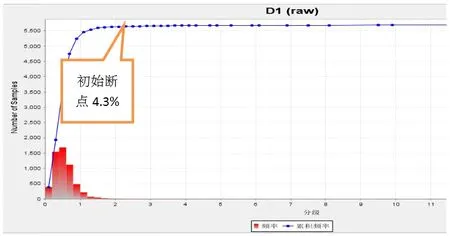
图5 组距=0.2%时频率累积曲线初始断点位置观察

随着组距加大，如组距分别取值0.001%、0.1%、0.2%，其初始断点呈现单调递增（图6）。

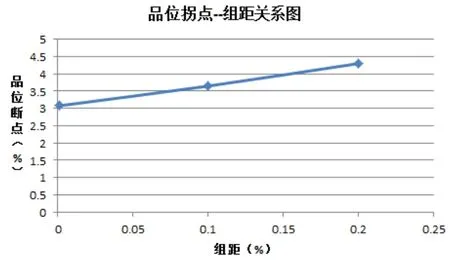
图6 断点值与组距之间关系

综合上述，有以下规律：

（1）本例当矿体样本品位服从或近于服从同一正态概率分布时，可以用频率累积曲线靠近确定累计曲线初始的断点（拐点）值，该值基本和我国传统处倍数法所确定的特高品位值接近；

（2）本例数理统计法值水平估值法确定特高品位值，要合理确定水平。当按5%水平进行特高品位估值时，其值明显低于传统倍数法。

（3）品位断点（即拐点）与组距关系密切，随着组距加大而增大。

5 结论

通过传统法和数理统计法处理特高品位的研究对比，探讨了二者之间各自的数据结构特点及内在联系，初步结论如下：

（1）传统倍数法按品位变化系数及均值的6倍～8倍界定特高品位，是否经过了数理统计分析尚不得而知。但本例通过与频率累积曲线初始断点（即拐点）比较，该法确定的特高品位界限值与频率累积曲线上的初始断点（拐点）基本相对应，即二者具有较好的相合性，殊途同归。

（2）本例频率累积曲线初始断点（拐点）具有易于鉴别的特点，但需注意，作图时的组距要尽可能地小，才能客观反映品位数据的特点，不可人为地为了少处理数据而有选择性地增大组距，从而人为“创造”特高品位。

（3）统计法处理特高品位，多种出版物选取a=5%水平来估值，但其估值和传统法比较有显著差异，表现在取值太低，处理样品数过多。本文探讨了置信水平接近极限状况（即正态函数表中估值最大系数3.48），其值仍远低于传统倍数法，处理样品数远高于倍数法，故建议谨慎用之。

（4）建议处理特高品位采用截值法（消值法）而不是平均品位代替法，这样能更好地反应自然规律，而不至于本来特高值被均值代替后，却低于临近值的不合理情形。

（5）任何特高品位的处理，首先要符合地质规律，如果特高品位连成片且规律明显，不要机械地套用任何特高品位处理方法，而要考虑在合理情况下圈定富矿段(体)，单独圈矿算量。