基于啮合刚度的机车牵引齿轮变形量研究分析

雷 蕾 ，丁海春 ，轩 亮

（1.大连交通大学机械工程学院，辽宁 大连 116028；2.江汉大学机电与建筑工程学院，湖北 武汉 430056）

1 引言

近年来，我国高速铁路技术取得长足的发展。国务院常务会议审议并原则通过《中长期铁路网规划》，为机车产业的加速研发提供了一个巨大的契机。牵引齿轮作为机车传动装置的核心组成部分，主要功能就是将牵引电动机的输出扭矩传递给轮对，使机车能够正常安全运行。故牵引齿轮啮合的合理与否对机车振动噪音以及安全运行有很大的影响。目前齿轮的研制正朝着高速、重载的趋势发展，但由于动载荷等因素产生的影响却成为这种趋势的绊脚石，造成这些问题的主要原因还是在于啮合误差，引起啮合误差的影响因素主要有两个方面：（1）齿轮的制造误差；（2）齿轮接触受载后产生的弯曲、接触等变形。齿轮的制造误差主要包括基节误差和齿形误差，但目前的工业生产中已经有很高效的手段将其控制在许可范围内，然而对于齿轮变形量的计算，在齿轮传动过程中，齿轮受载情况比较复杂，计算也就比较复杂[1]，常用的齿轮变形量计算方法主要有数值计算法以及有限元法，有限元法虽然计算精度比较高，但不适合于参数化设计，将以一种比较便捷的方法即从啮合刚度的角度出发计算牵引齿轮的变形量，为后续的齿廓修形打下基础。

2 变形量计算的理论分析

2.1 啮合刚度

齿轮综合啮合刚度的精确计算是进行轮齿修形、动态特性仿真、机械故障诊断及检修以及齿轮参数优化设计的重要基础和首要前提。在进行齿轮修形时，啮合刚度贯穿整个计算过程。一般情况下，齿轮的重合度都不为整数，在啮合过程中同时参与啮合的轮齿对数也是不断变化的，并且随时间呈周期性变化，这就导致齿轮轮齿从齿根到齿顶的弹性变形量处处不同。与啮合齿对数变化规律类似，轮齿弹性变形量也是随时间变化的函数，同时也可以表征为载荷作用角的变化函数。

对于直齿圆柱齿轮，齿轮随时间变化的啮合齿对数与端面重合度εα有关。对于一个端面重合度为（1～2）之间的齿轮副，总可以将啮合区域分为单齿啮合区和双齿啮合区，而在双齿啮合区，由于两对齿同时啮合，综合刚度就是两对齿的刚度之和。由于单、双对齿的交替运行，齿轮综合啮合刚度也是随时间或载荷作用角变化的周期函数。图中：B、D—单双齿啮合区的分界点；A、E—大、小齿轮的齿顶啮合点；C—节点，如图1所示。

图1 单、双对齿啮合区的边界条件划分Fig.1 Boundary Conditions of Single and Double Mating Regions

关于齿轮啮合刚度的计算，目前主要有3类计算方法：材料力学法、弹性力学法以及数值解析法。但近年来随着计算机技术的发展，有限元法越来越频繁地被诸多专家学者应用于齿轮动力学研究中，从理论角度来看，材料力学法还是应用最广泛的一类方法，而其杰出代表：石川公式也广泛的应用于直齿轮啮合刚度的计算中。

直齿轮的啮合刚度可以根据石川公式求得，由于齿轮轮齿外形较为复杂，石川法就把它简化为简支梁，也就是一个梯形加上矩形的模型组合，如图2所示。从而解得轮齿各部分的变形。

齿轮轮齿变形主要包括当量齿形中矩形部分和梯形部分中的弯曲变形、剪切变形、基体弹性倾斜产生的变形以及齿轮对接触变形等，可以视为这些变形的综合。矩形部分的弯曲变形用符号δwj表示，梯形部分的弯曲变形为δwt，接触变形用δh表示，剪切变形为δS，基体弹性倾斜产生的变形为δG，总变形为δz，式中各变形量单位均为μm[2]。

图2 石川算法模型Fig.2 Ishikawa Algorithm Model

矩形以及梯形部分的弯曲变形公式可以根据弯矩公式结合卡氏定理推导出[2]，如下：

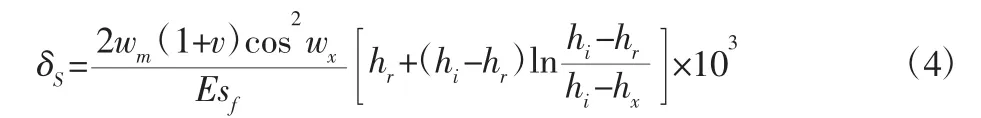
式中：wm—齿宽方向的平均线载荷；v—泊松比；E—齿轮材料弹性模量；h—齿轮轮齿高度；hx—啮合点高度，模型，如图3所示。wx—载荷作用角，数学模型，如图4所示。可以根据压力角αx求得，具体公式如下：

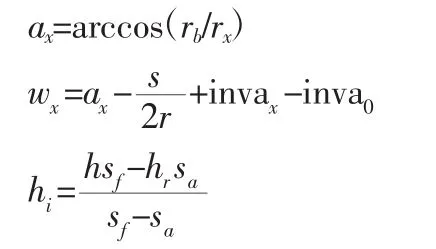
剪切变形公式也可以以虚功原理为基础推导得出：

图3 啮合点高计算Fig.3 Calculation of Meshing Point

图4 载荷作用角计算模型Fig.4 Load Angle Calculation Model

对于齿轮的接触变形，需要考虑到主、从动齿轮接触线处的曲率半径，而曲率半径可以根据Hertz公式求出。一对渐开线齿轮啮合，其轮齿齿廓的接触，可以看做是以两齿廓在接触点处的曲率半径的两圆柱体相接触，如图5所示。

假设接触线宽度设为2s，ρ1，ρ2分别为主、从动齿轮接触线处的曲率半径，由赫兹接触理论可知：

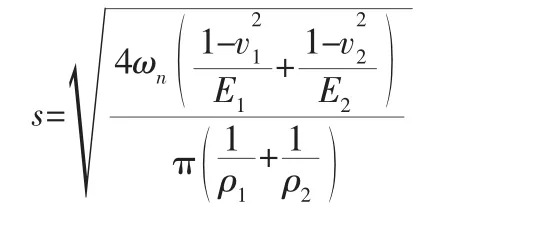
由此可以推导出接触变形的公式[2]：

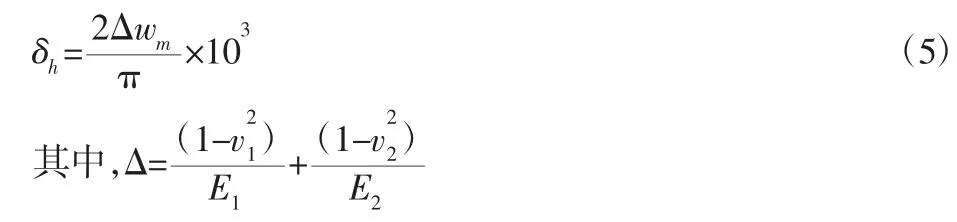
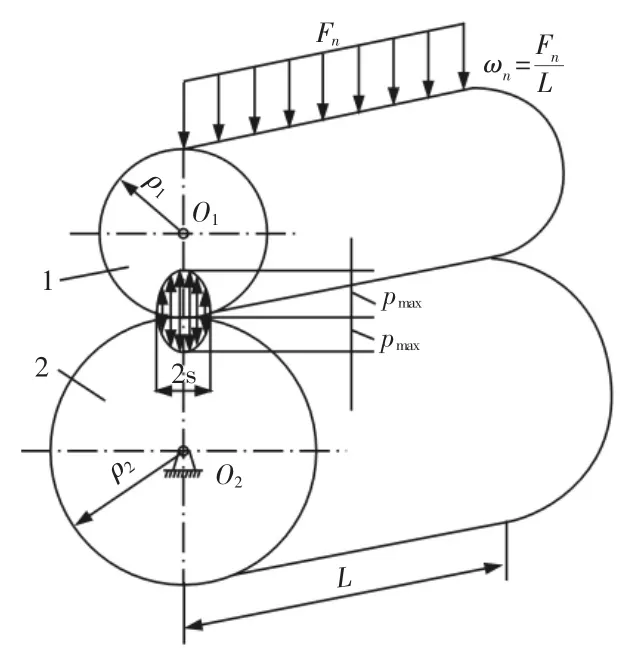
图5 赫兹接触模型Fig.5 Hertz Contact Model

基体弹性倾斜产生的变形可以根据参考文献[2]利用弯矩以及半无限弹性体平面弹性力学分析推导得出。

对于斜齿圆柱齿轮，它的轮齿啮合过程是从轮齿的一端开始，然后逐渐扩展到整个齿面，最后从齿轮的另一端完全退出啮合，这种渐变的形态直接决定斜齿轮在n和n+1对齿啮合交替不再是突变的，也决定斜齿轮的时变啮合刚度变化规律在本质是与直齿轮有很大的差别，直齿轮在单双齿交替啮合时会出现阶跃性变化，而斜齿轮则是围绕某个值较小范围地上下浮动。由斜齿轮啮合原理可知齿轮的单对齿有效接触线长度先增加，然后保持一段时间，最后逐渐降低到0，直至退出啮合。

对斜齿轮啮合刚度的求解方法国内外专家学者也进行了大量的研究，但由于斜齿轮结构的复杂性，包括端面和法面的存在，目前没有准确、统一的计算公式或标准，主流的方法有2种：①先根据公式得到局部啮合刚度，进而通过离散点的求和得到最终的啮合刚度曲线；②利用傅里叶级数的拟合。

局部啮合刚度：

式中：fbj（ikS）—弯曲变形影响系数—高斯求积公式系数；fcj（ikS）—接触变形影响系数；P（jkS）—第j对齿作用于啮合位置S，作用在接触线任意K点的力的大小。

单对齿啮合刚度：

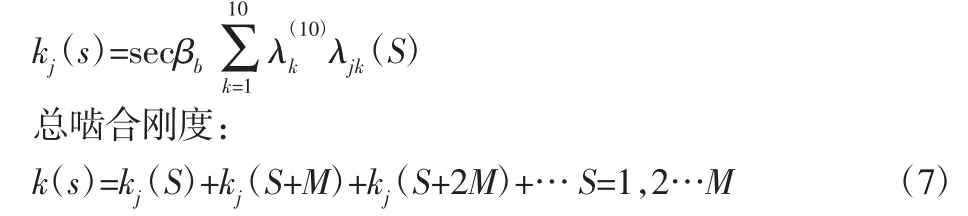
但参照斜齿轮啮合刚度变化曲线可知，其曲线可以通过傅里叶级数拟合出来[3]。通常先计算出刚度的峰值以及平均值，再根据啮合频率将刚度曲线近似为周期函数，略去高阶项即为拟合后的刚度曲线：

式中：km—平均刚度；kl—刚度峰值；φj—对应的相位角；wn—轮齿啮合的圆周频率，具体计算公式如下：

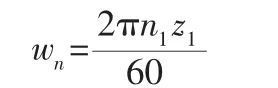
式中：n1—主动轮转速；z1—主动轮齿数。

2.2 齿间载荷分配

对于重合度在（1～2）之间的齿轮而言，啮合过程始终处于单双齿交替啮合。在单齿啮合区仅有一对齿参与啮合，轮副传递的载荷由这对齿全部承担，故不存在载荷的分配问题，而在双齿啮合区，载荷则由两对齿共同承担，齿间载荷分配问题可以利用动力学等效为同时相并联的两根弹簧共同承担载荷的分配问题[4]，因为轮齿啮合刚度是时变的，故载荷分配系数也是时变的。载荷分配比例公式如下：

式中：φ1、φ2—双齿啮合区同时参与啮合的齿对1和齿对2的载荷分配比例；k1、k2—啮合齿对1和啮合齿对2的综合啮合刚度；Δ1、Δ2—齿对1和齿对2的修形量大小；wm—齿宽方向平均单位线载荷。

根据牛顿第三定律作用力与反作用力可知，同一啮合对中主、从动齿轮承担的载荷大小一样。由于齿轮转矩在功率和转速都确定的情况下恒为定值，故总载荷大小保持不变，双齿啮合区同时啮合的两齿对也满足力的协调方程：

3 案例分析

案例以SS8-Ⅱ型机车牵引齿轮为研究对象利用啮合刚度求解高速重载机车牵引变位齿轮的变形量。机车单轴运行功率为900KW，电动机高速运行转速为1946r.min-1。SS8-Ⅱ型机车牵引齿轮的基本参数和部分几何尺寸，表格中的单位均为mm，如表1所示。

表1 机车齿轮基本参数和部分几何尺寸Tab.1 Basic Parameters and Some Geometric Dimensions of Locomotive Gear

由于SS8-Ⅱ型机车牵引齿轮为直齿轮，啮合刚度可以根据石川公式求得，将齿轮双齿啮合区分为若干段，依次计算出每个啮合点的刚度，实例将单齿啮合区等分为20段，将双齿啮合区各等分为30段，在双齿啮合区，两对齿轮同时啮合，故综合啮合刚度为两齿轮啮合刚度之和。在单齿啮合区，啮合刚度可以看成单对齿刚度，图6为齿轮啮合刚度曲线。计算结果，如表2所示。

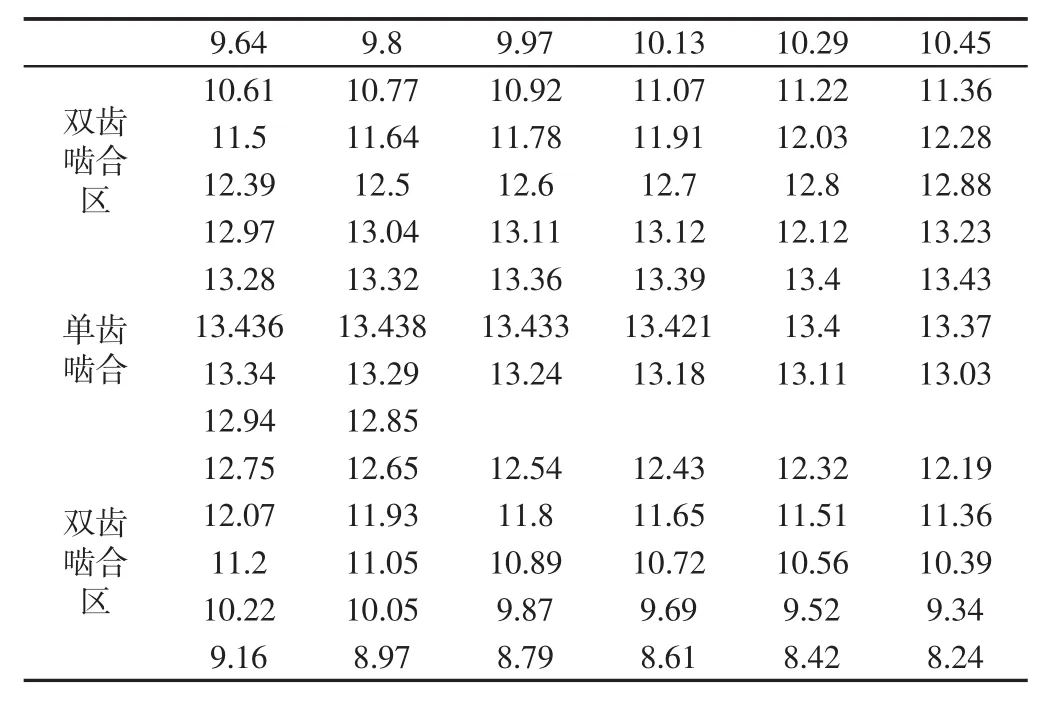
表2 各啮合点上的啮合刚度（单位为N/（mm·μm））Tab.2 The Meshing Stiffness at Each Engagement Point

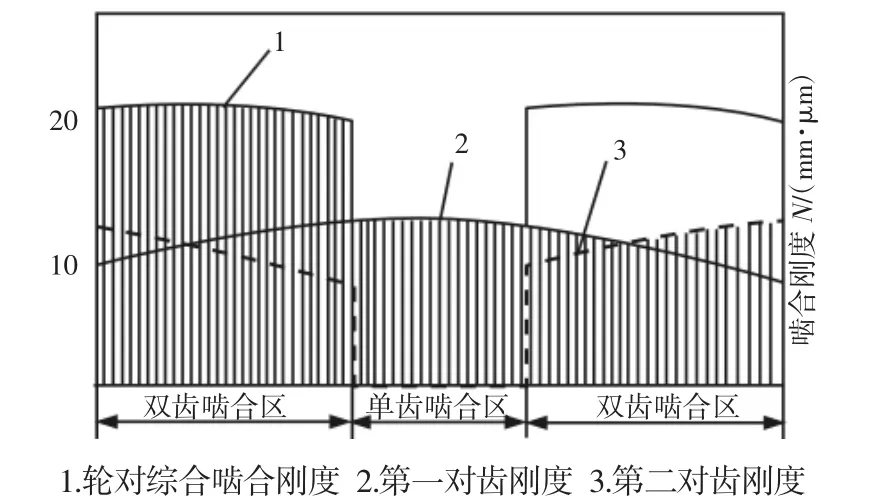
图6 各对齿啮合刚度Fig.6 Meshing Stiffness of Each Pair of Teeth

由机车单轴运行功率以及电机转速可以求得齿轮所受法向力FN=25699.7N，由于主、从动齿轮齿宽不相同，需要取两者较小值作为工作齿宽带入计算，单位齿宽平均线载荷为229.46N/mm。在单齿啮合区，由于一对齿承担全部载荷，故齿间载荷分配率为100%，在双齿啮合区，则需要根据两对齿的啮合刚度比得到载荷分配率，继而求出主、从动轮啮入啮出时的单位齿宽线载荷。SS8-Ⅱ型机车牵引主动齿轮齿间载荷分配，如表3所示。示意图，如图7所示。

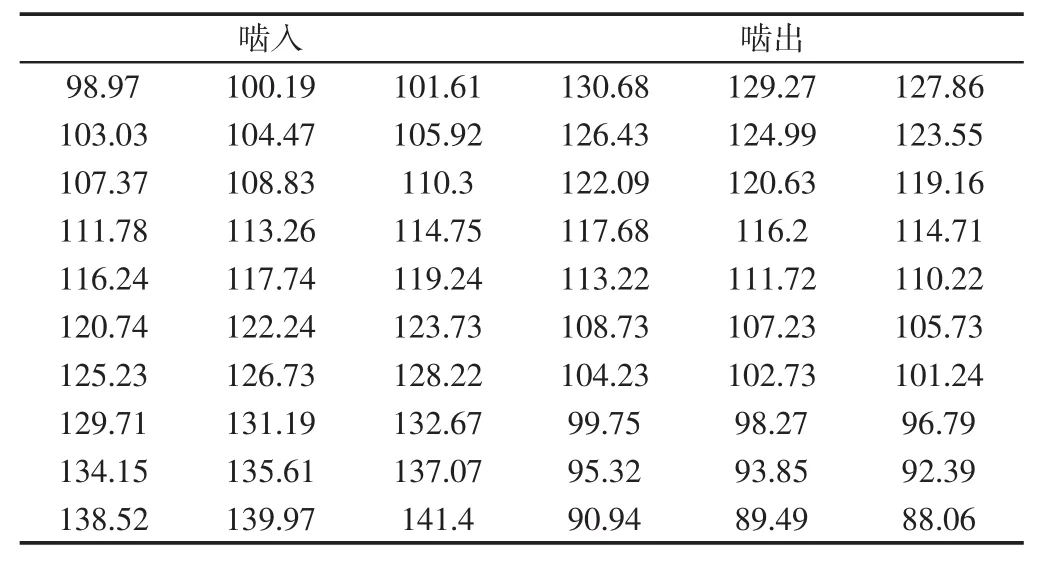
表3 主动齿轮齿间载荷分配（单位为N/mm）Tab.3 Interdental Load Distribution on Driving Gear

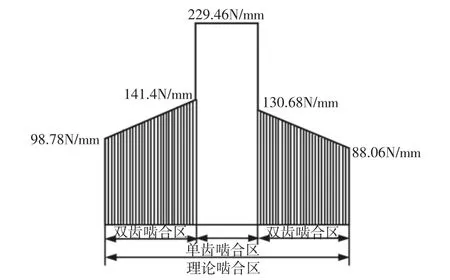
图7 主动齿间载荷分配示意图Fig.7 Diagram of Load Distribution on Driving Gear

李润方在《齿轮传动的刚度分析和修形方法》一书中著道：在双齿啮合区，每对齿轮各自承担一部分载荷，齿间载荷分配涉及到时变啮合刚度以及误差等因素，考虑到接触、弯曲、剪切以及基体倾斜所引起的变形，其载荷分配大致按照40%～60%～100%～60%～40%的值变化[5]。本实例的趋势变化为43.13%～61.6%～100%～56.87%～38.4%，大致上与李润方推导出的齿间载荷分配一致。

若对主、从动齿轮同时修形，还需同时计算主、从动齿轮单齿刚度。主从动齿轮的轮齿刚度也可以根据石川公式求得。由计算结果可知，主动齿轮单齿啮合刚度随啮合点位置高度的增大而减小，而从动齿轮单齿啮合刚度随啮合点位置高度的增大而增大。主动齿轮的单齿对刚度，如表4所示。其示意图，如图8所示。

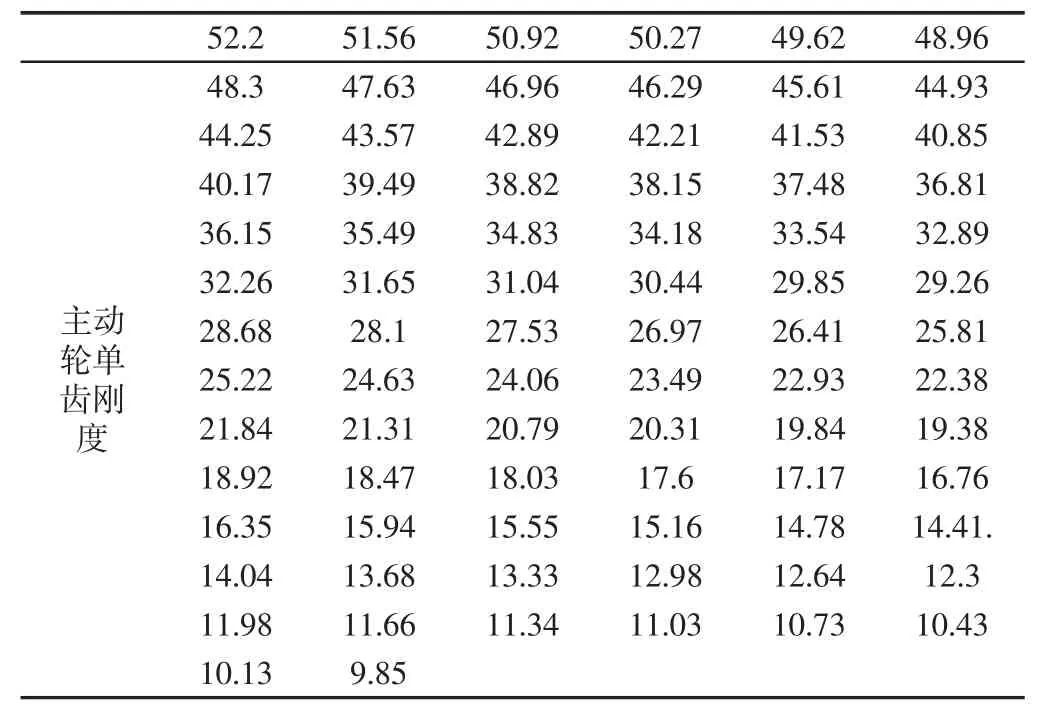
表4 主动齿轮的轮齿刚度（N/（mm·μm））Tab.4 Gear Stiffness of Driving Gear（N/（mm·μm））

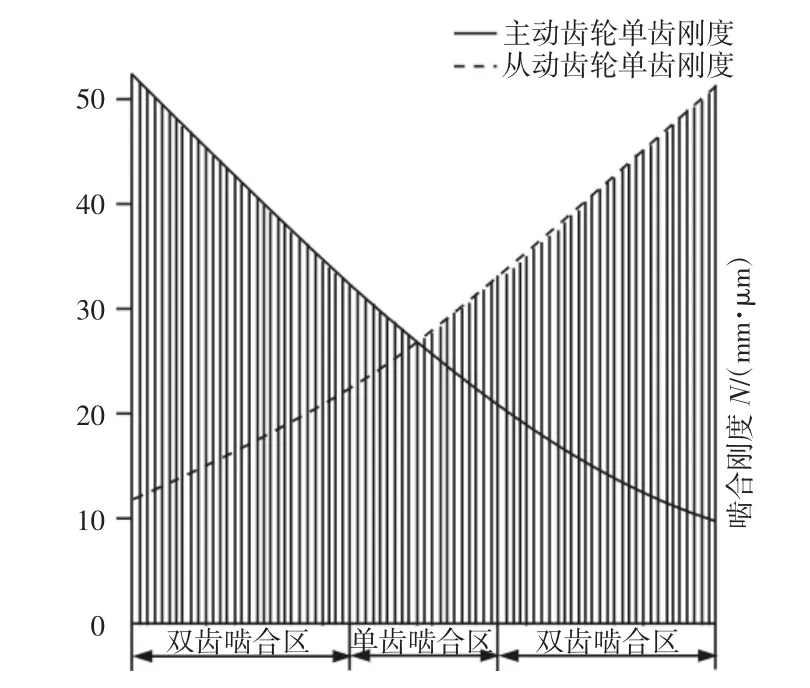
图8 主从动齿轮的轮齿刚度示意图Fig.8 Diagram of Stiffness on Drivingand Driven Gear

根据上面求得的齿间载荷分配以及主从动齿轮的轮齿刚度可知主从动齿轮的变形量，主动轮变形量，如表5所示。从动轮变形量也可以根据此方法求出。主从动齿轮变形量示意图，如图9所示。

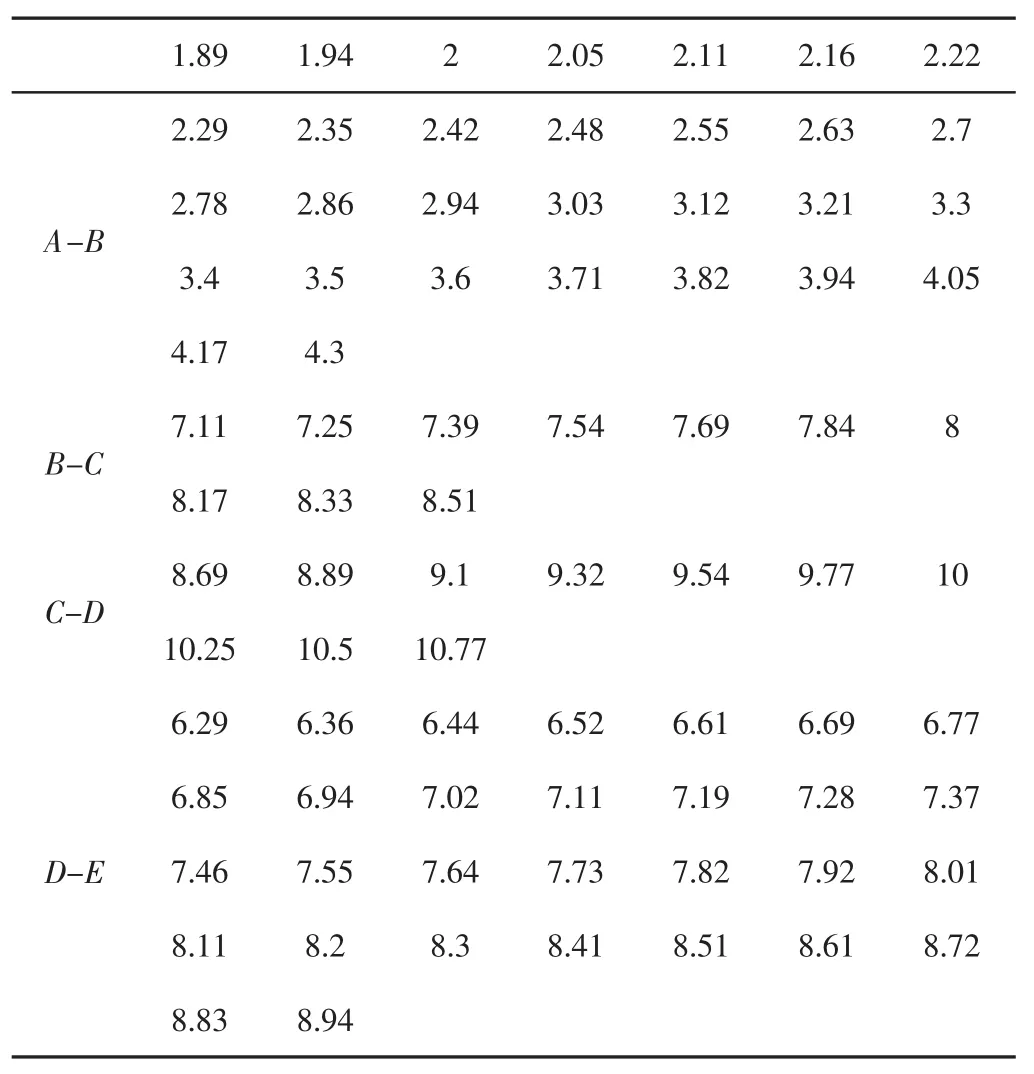
表5 主动轮变形量（μm）Tab.5 The Deformation of Driving Gear（μm）

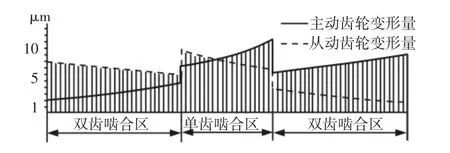
图9 主从动齿轮变形量示意图Fig.9 Diagram of the Deformation on Drivingand Driven Gear

由表格数据及示意图可知：主动齿轮变形量随啮合点高度呈增长趋势，但在单齿啮合区过渡到双齿啮合区及在双齿啮合区过渡到单齿啮合区时会出现突变，主要原因是由于在单齿啮合区时只有一对轮齿承担全部载荷，而在双齿啮合区只承担部分载荷，但在齿对整个啮合过程中刚度变化比较平滑，没有出现突变。从动齿轮的变形量则与主动齿轮变化趋势相反。

4 结论

（1）基于时变啮合刚度计算得到的齿间载荷分配与已有根据经验公式及大量实验数据所得的曲线图大致一致，从间接验证在双齿啮合区利用综合啮合刚度之比确定齿间载荷分配的方法可行。

（2）数据表明齿间载荷分配在单齿啮合区过渡到双齿啮合区及在双齿啮合区过渡到单齿啮合区时会出现突变，单齿啮合刚度随啮合点位置变化比较平滑，总体来说，主动齿轮变形量随啮合点高度呈增长趋势，但在过渡区也会出现阶跃性突变，从动齿轮则与之相反。

（3）实例结果表明：从啮合刚度的角度出发计算牵引齿轮的变形量可以很好地应用于变位牵引齿轮，而且非常方便进行参数化设计。