一种基于小波包变换和监督NPE的滚动轴承故障诊断方法
2020-03-27丁恩杰吴守鹏
董 飞 ,俞 啸 ,3,丁恩杰 ,吴守鹏
(1.中国矿业大学信息与控制工程学院,江苏 徐州 221008;2.中国矿业大学物联网(感知矿山)研究中心,江苏 徐州 221008;3.徐州医科大学医学信息学院,江苏 徐州 221009)
1 引言
滚动轴承作为旋转机械设备的关键部件之一,其发生故障会严重影响到旋转机械的安全稳定运行[1]。因此,进行滚动轴承的状态监测与故障诊断对保障安全生产和降低维护成本具有重要意义。近年来,随着信号处理、数据挖掘以及人工智能的快速发展,基于数据驱动的方法在滚动轴承故障诊断中变得越来越重要,其主要可分为四个步骤:信号处理,特征提取,特征降维和故障模式识别[2-3]。
滚动轴承在运行过程中的振动信号蕴含着丰富的状态信息,是轴承故障状态分析与诊断的有效手段[2]。小波变换是分析非线性、非平稳振动信号的有效方法,但是由于小波变换没有对信号的高频部分做进一步的分解,容易导致高频部分故障特征信息的丢失。针对此问题,在小波变换的基础上,小波包变换被提出,它能进一步分解信号在高频区的细节系数,提供更详细、更全面的时频面。文献[4]将小波包分解及其能量谱用于发动机连杆轴承故障诊断;文献[5]将小波包能量特征与径向基函数网络相结合,建立了滚动轴承故障监测模型;文献[6]通过计算小波包提取的信号包络谱的峰值,增强信号峭度特征,用于微弱瞬时信号的监测。
结合小波包变换与统计参数可得到高维原始特征集。然而,由于故障类型与统计特征之间存在复杂的映射关系,原始特征集中存在干扰和冗余特征,可能会影响故障诊断的准确度。因此,提出一种基于朴素贝叶斯的故障敏感特征选择方法(Features Selection Based on Naive Bayes,FSNB),实现对原始特征集中单个统计特征的故障敏感度的量化分析,筛选出故障敏感度较高的统计特征进行故障诊断。
在特征降维方面,领域保持嵌入(Neighborhood Preserving Embedding,NPE),是一种非监督的线性降维方法,其主要目标是保持数据流行中的局部结构。LDA作为一种经典的线性降维方法,其可以将故障的类别信息考虑到特征降维过程中。因此可以结合NPE与LDA各自的优点,提出一种改进的特征降维方法,基于类别标签的监督邻域保持嵌入方法(Supervised Neighborhood Preserving Embedding with Label Information,SNPEL),以此来提高故障诊断的精度与适应性。
在故障模式识别方面,采用KNN方法。KNN是一种经典的非参数分类方法,在模式识别领域得到了广泛的应用。文献[7]利用局部均值分解和KNN实现滚动轴承故障诊断。文献[8]利用模糊K近邻支持向量进行数据描述,从而实现水电机组振动故障诊断。
首先利用WPT分解振动信号,得到终端节点的单支重构信号并计算其包络谱(Hilbert Envelope Spectrum,HES),随后结合统计参数,可得到原始统计特征集。然后利用朴素贝叶斯方法进行敏感特征的筛选,再利用提出的基于类别标签的监督NPE方法进行特征降维,得到新的特征集并用于训练KNN分类器。最后,已训练的分类器用于对测试数据进行故障诊断。实验分析结果表明,该模型可以达到比较理想的滚动轴承故障识别效果。
2 基于朴素贝叶斯的故障敏感特征选取(FSNB)
2.1 朴素贝叶斯算法
朴素贝叶斯算法是基于贝叶斯定理的分类方法。根据已有的样本数据实例,运用贝叶斯公式来判定待测数据的归类问题。贝叶斯算法的主要思想是将事件的先验概率和后验概率相联系,并利用先验信息预测事件的后验概率。朴素贝叶斯算法还具有自学习能力,可以将新数据记录加入到已知的先验信息中,从而进一步影响事件的后验概率,提高事件预测的准确性。
贝叶斯公式如下:

式中:P(A|B)—条件B下A的后验概率;P(A)—A的先验概率;P(B|A)—条件A下B的后验概率;P(B)—B的先验概率。
令训练样本为 X={x1,x2,…,xn},每个样本对应的类别为label(xi)∈C,其中C={c1,c2,…,cm}表示类别集合,T={t1,t2,…,tn}为测试样本。
样本T归属于类cj的后验概率为:
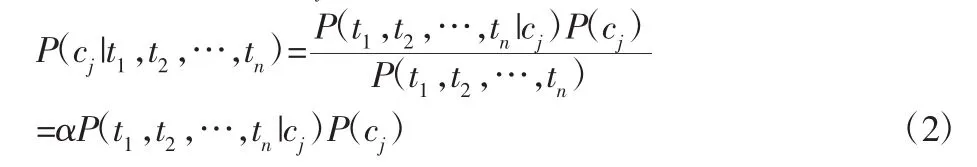
式中:P(cj|t1,t2,…,tn)—测试样本归入故障类型 cj的后验概率;P(t1,t2,…,tn|cj)—故障类型 cj的条件概率;式中 P(cj)为故障类型 cj的先验概率;α=1/P(t1,t2,…,tn),α 为常量。朴素贝叶斯算法根据式(2)计算出全部类 cj,j=1,2,…,m 的后验概率,然后将测试样本中数据归入后验概率最大的类中。朴素贝叶斯是以各属性变量间相互独立的条件为基础,因此,式(1)中的后验概率的计算可以变换为:
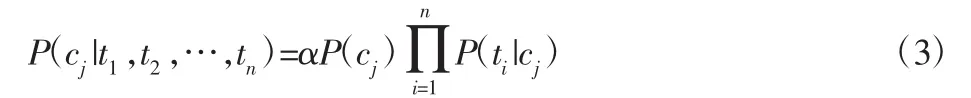
2.2 故障敏感特征选择
在训练样本中,共有M种故障类型,每种故障类型有N个样本,每个样本有K种统计特征。故障敏感特征选择的目标是从K种统计特征中选择出对故障类型较为敏感的特征,然后组成新的特征集。对于每种统计特征,利用朴素贝叶斯算法对其样本进行分类,分类的精度作为衡量其故障敏感程度的指标。
经信号处理和统计参数计算,可以得到原始特征集[FS1,FS2,…,FSK],其中 FSk如下所示:


图1 训练集样本Saccuracy序列值分布Fig.1 Saccuracy Sequence Distribution of Training Samples
然后,利用朴素贝叶斯算法对每种故障状态样本分别进行分类,得到分类精度Accurac,将 Saccuracy(k)=Accurac作为第k种统计特征对故障敏感程度的衡量指标。可以得到一个分类精度和的序列Saccuracy={Saccuracy(1),Saccuracy(2),…,Saccuracy(K)}。最后,对分类精度和的序列进行降序排列。我们认为Saccuracy(k)值越大,说明该统计特征对故障敏感程度越高,更适合用于故障诊断与分类。训练集样本Saccuracy序列值分布,如图1所示。
3 基于类别标签的监督邻域保持嵌入(SNPEL)
提出了一种基于类别标签的监督NPE方法,该方法的目标是可以在保持高维数据局部几何结构不变的同时,通过融合LDA的优化目标,构建出一个新的优化目标函数。使得在降维过程中考虑了类别标签信息,获得判别性较强的低维表示,从而更有利于故障诊断与分类。
令训练样本为 X={x1,x2,…,xn},其中 xi∈Rm,n 训练样本的个数,m为训练样本的维数。每个样本对应的类别为label(xi)∈C,其中 C={c1,c2,…,cm}表示类别集合。寻找一个映射矩阵 A={a1,a2,…,ad},其中 ai∈Rm,d 为将训练样本进行映射之后的维度,将Rm空间的数据映射到一个相对维度较低的特征空间Rd(d≤m)中。数据点xi在Rd中的表示为yi,且yi=ATxi。
SNPEL的第一个优化目标是保持数据集的局部邻域流行结构不变,构造训练样本上的近邻图时采用的方法和LLE相同。令xi的近邻集合为knn(xi),其近邻图重构权重系数矩阵W满足下面要求[9-10]:

对于非0的权重系数,需要通过最小化重构损失函数求得:
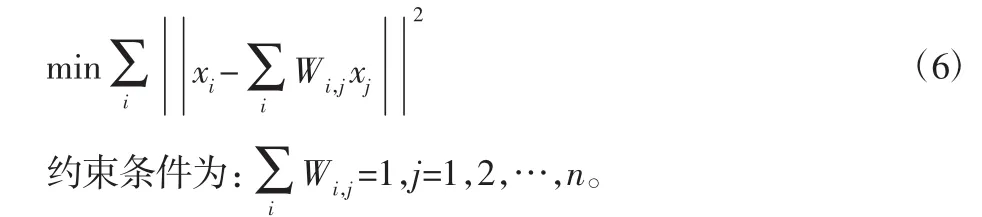
当W可以在Rm空间中重构出数据点xi,那么在Rd空间中也可以重构对应的点yi。所以映射矩阵的求解可以转换为求解下述最小化问题得到:
SNPEL的第二个优化目标是最大化类间散度和最小化类内散度,来获得判别性较强的低维表示。其中,类间散度矩阵Sb和类内散度矩SW阵定义如下:

式中:cl—第 l类样本集合;μl—第 l类样本均值;μ—所有样本均值。类间散度矩阵Sb和类内散度矩阵SW的等价形式如下:

式中:Pb=、PW=—权值矩阵;Db、DW—n×n 的对角矩阵,从上式中可以看出和中体现类别的判别信息。于是,SNPEL的第二个优化目标可归结为下面的优化问题:

利用式(7)来保持样本原有的局部几何结构,利用式(14)和式(15)实现最大化类间散度和最小化类内散度,结合式(7),式(14)和式(15),可得SNPEL的优化目标函数如下:
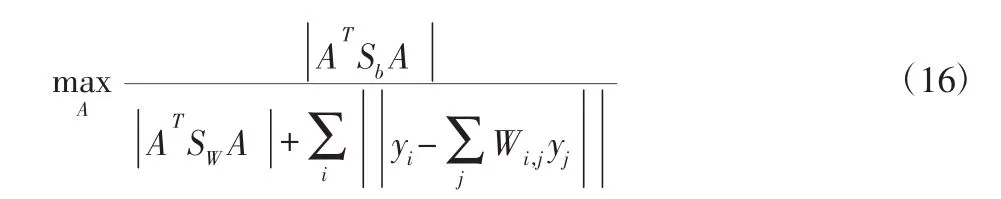
结合式(10)和式(11),可改写成迹比优化形式:
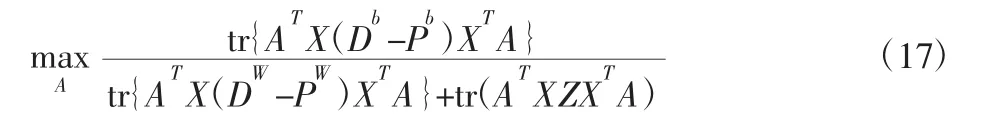
式中:Z=(I-W)T(I-W),I=diag(1,…,1),对于上式,还需要对分母
进行归一化,因此优化目标函数最终为:

式中:(DW-PW)nor、Znor—经过归一化后的矩阵。最终,SNPEL 的目标函数优化问题转化为下面的广义特征值求解问题:

其中,L=(DW-PW)nor,S=(DW-PW)nor+Znor。假设是式(19)特征值λ0≥λ1≥…≥λM所对应的特征向量,则用于降维的映射矩阵由前 d 个特征向量组成,即 A={a1,a2,…,ad}。因此,给定 xi∈Rm,可以得到其相应的映射变换 yi∈Rd:xi→yi=ATxi。
4 系统框架

图2 故障诊断方法系统结构示意图Fig.2 System Structure of the Fault Diagnosis Method
所提出的故障诊断方法系统结构,如图2所示。整个故障诊断过程分为四个步骤:信号处理,特征提取,特征降维和故障模式识别。在第一步中,原始振动信号经WPT处理,得到终端节点的单支重构信号并计算包络谱,结合统计参数,得到原始特征集;第二步中,将原始特征集经过基于朴素贝叶斯的故障敏感特征选取方法处理,得到故障敏感特征。第三步中,对于训练样本的高维特征集,利用SNPEL方法,得到低维特征集,并作为分类器的输入,同时还得到降维映射矩阵,直接用于测试样本的高维特征集降维。第四步中,将从训练样本中得到的低维特征集用于训练分类器,训练好的分类器直接运用于测试样本的故障诊断。
5 实验结果分析
5.1 实验设置与案例
使用美国凯斯西储大学滚动轴承数据中心的轴承振动数据,驱动端采用型号为6205-2RS JEM SKF的深沟球轴承,故障类型有滚珠故障、内圈故障和外圈故障,故障尺寸有0.007英寸,0.014英寸,0.021英寸和0.028英寸。电机的工作负载范围是(0~3)hp,对应转速为1730到1797r/min。正常情况在内的12种故障模式,如表1所示。从每种故障模式中提取60个振动信号样本,每个样本包含2000个连续的数据点。由于滚动轴承在实际工作环境中,其负载是变化的,处于变工况状态。因此为了验证提出故障诊断算法在变工况状态下的有效性和适应性,设计了四个验证案例。有两组对比实验,每组中均是采用一种电机负载的样本做训练集,不同电机负载的样本做测试集。其中,案例1和案例2均采用2hp样本作为训练集,案例1使用2hp的样本为测试集,案例2使用3hp的样本为测试集。案例3和案例4也是类似的对比实验,其不同在于采用3hp的样本作为训练集。
5.2 结果分析

表2 统计参数Tab.2 Statistical Parameters
利用WPT处理原始振动信号,在实验中,选用“db5”小波,经四层小波包分解得到的16个终端节点信号的单支重构信号,再分别计算出其希尔伯特包络谱,结合表2所示的6个统计参数,可以得到96个时域统计特征和96个包络谱统计特征,共192个统计特征,构成原始特征集(OriginalFeatures Set,OFS)。利用FSNB方法计算得到的训练集样本Saccuracy序列值分布,如图1所示。说明不同的统计特征对于故障敏感程度不同,我们可以基于此选择出故障敏感度高的特征子集用于故障诊断,如表1、表2所示。
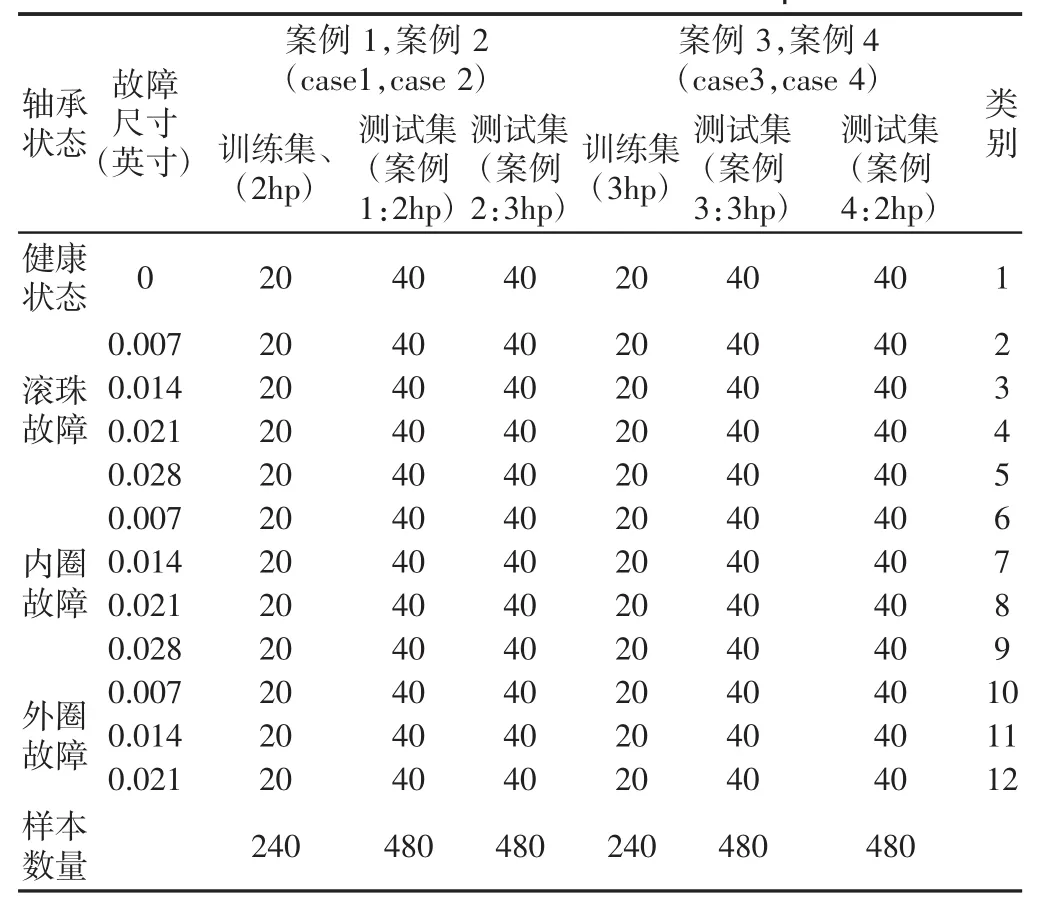
表1 实验中使用的振动数据集Tab.1 The Used Vibration Dataset in Experiments
分别对 OFS-KNN、OFS-FSNB-PCA-KNN、OFS-FSNBLDA-KNN和OFS-FSNB-SNPEL-KNN故障模型开展实验分析。这五个模型均是基于KNN的故障诊断模型,OFS-KNN是原始特征集(OFS)直接用于训练KNN。其余模型是首先将原始特征集进过FSNB敏感特征选择之后,将敏感特征分别使用PCA、LDA和SNPEL降维处理,结果用于训练KNN,最后将训练好的模型用于对测试样本进行故障诊断。四个案例所对应实验结果,每一个子图中是四种故障分析模型的精度曲线,横轴表示所选取的敏感特征数,纵轴是故障诊断的精度,如图3所示。


图3 四个故障诊断模型的实验结果Fig.3 Experimental Results of Four Fault Diagnosis Models
实验中PCA的降维大小为15,LDA的降维大小为11,SNPEL的降维大小为20。从图中可以看出,对于案例1和案例3,sfn在一定的范围内,四种故障分析模型均表现出较好的性能。对于案例2和案例4,sfn在一个较宽的范围内,OFS-FSNBSNPEL-KNN 表现出更好的性能,例如,sfn在(60~110)时,故障诊断的精度均可达到95%以上。因此,实验结果表明所提出的故障敏感特征选择方法FSNB与改进的降维方法SNPEL对于变工况下的滚动轴承故障诊断具有良好的效果与适应性,可应用于智能故障诊断系统。
6 结论
在对WPT、朴素贝叶斯以及NPE的研究基础上,提出一种基于朴素贝叶斯的故障敏感特征选择方法和监督NPE的特征降维方法,建立OFS-FSNB-SNPEL-KNN故障诊断模型,同时还设置了其他三种故障诊断模型(OFS-KNN,OFS-FSNB-PCA-KNN,和OFS-FSNB-LDA-KNN),实验分析结果表明:
(1)提出的FSNB方法,可以从时频分析得到的原始统计特征集中提取出故障状态敏感的特征分量,可以有效提高后续故障识别准确率;
(2)提出的SNPEL方法,可以实现降维过程中,既保持数据间集合结构不变,也最大化类间散度和最小化类内散度,从而得到更有利于故障诊断与分类的特征空间;
(3)对于OFS-FSNB-SNPEL-KNN故障诊断模型,选择合适故障敏感特征数量,可以获取较高的滚动轴承故障诊断识别率。
