基于三次样条插值法的干涉仪反射镜面型值误差分析

李 峰，汪杰君，熊显名，张文涛，杜 浩

（桂林电子科技大学 电子工程与自动化学院，广西 桂林 541004）

0 引言

集成电路产业是信息技术产业的核心，是支撑经济社会发展和保障国家安全的战略性、基础性和先导性产业，当前和今后一段时期是中国集成电路产业发展的重要战略机遇期和攻坚期[1]。光刻机，被誉为人类20世纪的发明奇迹之一，是集成电路产业皇冠上的明珠，研发的技术门槛和资金门槛非常高[2]。对于集成电路产业来说，高端制造是进行集成电路生产的基础。作为“国之重器”的高端光刻机，其研制是国家战略需求，国家科技重大专项“极大规模集成电路制造装备及成套工艺”明确将28nm浸没式光刻机产品作为专项的标志性目标成果。在光刻机的研究中，套刻精度一直是光刻机的重点和难点，而光刻机的测量系统则是关系到光刻机精度的重要环节。

图1 激光干涉仪测量原理图Fig.1 Measurement schematic diagram of laser interferometer

图2 运动台干涉仪测量系统结构Fig.2 Structure of interferometer measurement system

光刻机的运动台位移系统使用的是双频激光干涉仪进行测量位移[3]。双频激光干涉仪总体由两部分构成：光学系统和电路系统。光路系统由氦氖激光器、扩束镜、检偏器、光电接收元件、干涉镜等组成。双频激光干涉光路系统后续信号处理包括光电转换、放大整形、电子细分、连续计数、单片机和数码管显示等[4]。激光干涉仪测量系统的精度受多种因素影响，其测量误差主要包括：①系统误差，主要指受到激光干涉测量方法及测量系统元部件制造精度的限制；②阿贝、余弦误差，在测量系统安装过程中，测量轴线与被测对象的运动轴线之间的误差角以及测量过程中被测对象多自由度运动等形成的误差；③环境误差，干涉仪工作过程中，环境的波动（空气温度、压力及相对湿度的变化）引起空气折射率的变化，由此导致的误差；④延时误差，由干涉仪测量电路延时、测量数据滞后所产生的误差[5]。本文对系统误差进行了研究，主要是研究干涉仪中平面镜面型由于加工制造的缺陷产生的误差，根据激光干涉仪的测量原理，利用三次样条抽样法对干涉仪反射镜面型进行了仿真，最后算出了激光干涉仪反射镜面型值的误差。

1 激光干涉仪测量位移原理概述

1.1 激光干涉仪测量位移原理

激光干涉仪测量原理如图1所示。激光干涉仪测量系统包括：激光头（亥氖激光器、参考光接收器、偏振片、偏振分光器）、干涉测量装置（角隅棱镜、偏振分光片）、测量光接收器和激光计数卡。

激光器输出频差稳定的双频激光经过分光片M1分光，一束作为参考信号经过偏振片后变成频率为f2-f1的光直接由参考光接收器接收，另一束光则经过干涉测量装置中的偏振分光片M2后在a点分离成频率为f1和f2的光，频率为f2的光经过角隅棱镜M3的全反射，回到偏振分光镜的b点处；频率为f2的光经过四分之一波片后射入安装在运动台上的角隅棱镜，当运动台发生移动时，根据多普勒效应，由角隅棱镜返回的光的频率变为f1±△f，该光束与频率为f2的光在偏振分光片M2的b点处汇合，汇合后的光经过偏振片后变成频率为f2-f1±△f的测量光。根据干涉原理，参考光与测量光过激光计数卡的处理，即可计算出运动台的位移△L。

激光干涉仪的基本公式为：

其中，N=Δφ/2π，Δφ表示相位差，λ表示波长。

1.2 干涉仪测量位移系统

根据干涉仪测量位移原理，运动台干涉仪测量系统结构如图2所示，其中的干涉仪采用的都是双轴激光干涉仪。X向干涉仪的测量光束X1和X2与X向测量反射镜垂直，与运动台坐标系中的X轴平行；Y向干涉仪的测量光束Y1和Y2与Y向测量反射镜垂直，与运动台坐标系中的Y轴平行。Y向干涉仪的两条测量光束的测量值y1和y2可以计算出运动台的Y向位移y：Y=(y1+y2)/2，同时也可以测量出工件台绕Z轴的旋转度ΦYZ：ΦYZ=(y1-y2)/IF，IF表示双轴干涉仪中两测量光束之间的间距。同理，X向干涉仪可以测量出运动台X向的位移x：X=(x1+x2)/2，运动台绕Z轴的旋转度

图3 干涉仪反射镜实际面型Fig.3 Actual map of interferometer reflector

2 干涉仪反射镜面型校准

2.1 面型校准的原因

干涉仪的反射镜由于加工、装配精度、所受应力以及环境等因素的影响，其表面面形不可避免会存在一定的缺陷，即实际面形与理想面形存在一定的偏差，如图3所示。由于运动台定位控制时依赖于干涉仪的读数，从图中可以看出，若存在反射镜面形，会导致包括X、Y两个方向和Rz方向的测量值和台子的真实值不一致，导致运动台的定位出现误差，所以需要对干涉仪反射镜的面型进行测量校正以补偿测量误差。X向测量反射镜的位置x的不平整度的校正值YMX，旋转度ΦXZ修正值YΦZ；Y向测量反射镜的位置y的不平整度的校正值XMY，旋转度ΦYZ修正值XΦZ。

2.2 反射镜面型计算方法

如图4所示，首先由X向干涉仪控制ΦXZ保持不变（设置为零），由Y向干涉仪控制工件台在Y方向保持零位，工件台在X轴方向进行往返运动，让Y向干涉仪能读取到整个Y向反射镜的面形读数，如此可以测量得到在不同X位置处的面型值XΦZ的值。工件台在最左端时如图中绿色图形所示，在右端时如图中红色图形所示。干涉仪X向反射镜面型向校准方法同Y向反射镜面型校正方法一样。

平移面形的计算基于旋转面形，涉及到局部面形结构，干涉仪光束和局部面形之间的结构示意图如图5所示。在干涉仪光束Y1测量j点的同时，Y2测量了j+1的点面形值，它们之间的间隔为IF。同时，基于之前的旋转面形XΦZ，可以得到j点处的旋转面形值Mj。由图中的几何关系可得到Y向不同X处的面型值为：

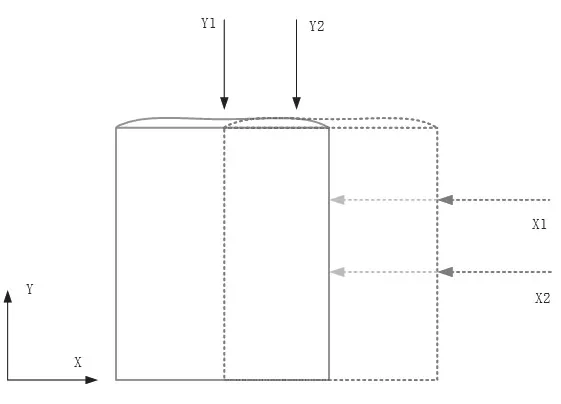
图4 反射镜面型计算原理Fig.4 Calculation principle of interferometer reflector

图5 干涉仪光束之间结构示意图Fig.5 Schematic diagram of interferometer beam structure

2.3 公式推导

工件台在X=0处沿Y向运动，根据第i个测量点的旋转偏移量Mi，可得该点的旋转面形，具体推导过程如下：

如图5所示，定义函数M(y)是描述X反射镜在y位置处关于面形的连续函数，x1mea(y)和x2mea(y)为在不同的Y向位置干涉仪光束实际测量的值，那么X向干涉仪测量得到的真实值分别为：

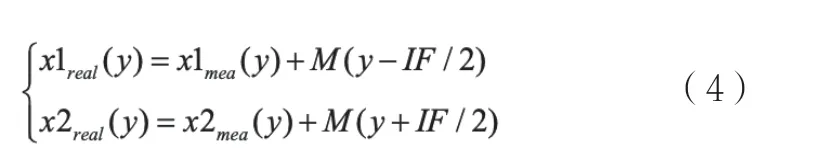
而工件台位置和旋转的真实值如下：

由此可以得到：

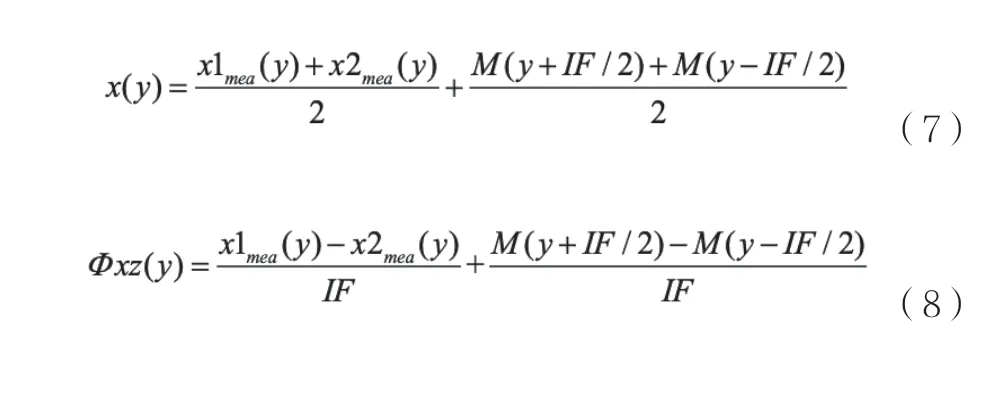
真实的测量位置x和旋转ΦXZ为未校正的测量结果与面形校正值之和，即：

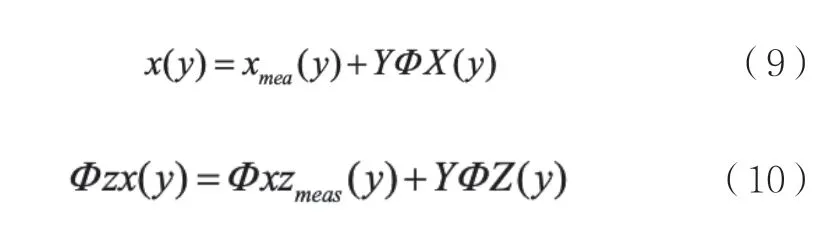
其中有：

3 仿真实验与分析

3.1 三次样条插值算法

对于一组离散的数据yi=y(xi)，i=1,2,3...N，其三次样条曲线S(x)满足如下条件：

1）S(x)是分段曲线，在每一个分段区间内部[xi，xi+1]，S(x)=Si(x)是一个三次曲线。

2）在每一个xi处，S(xi)=yi

3）S(x)的一阶导数S'(x)和二阶导数S"(x)在整个区间[x1，xN]内连续；则对每一个区间内的样条曲线的分段函数可以表述为：

其中，ai，bi，ci，di代表4N个待求系数，由前述3个条件可得如下表达式：

图6 YMX的仿真结果Fig.6 Simulation result of YMX

其中：

可将上述方程写成矩阵的形式：

限定边界条件为m0=0和mn=0。

对于如上矩阵，根据三角矩阵的解法，直接可得：

3.2 模型仿真

如图6所示，为本文设计的模型仿真的结果图，主要是针对X向反射镜面型的仿真，使用的软件是Matlab R2015b。首先，设置了一个模拟真实面型的函数M(y)，然后模拟了运动台的Y向运动轨迹，根据运动轨迹进行测量点的数据采集，根据公式可以模拟出工件台位置，然后利用三次样条插值算法对这些数据进行处理，最终可以模拟出测量到的面型值。

图7 XΦZ的仿真结果Fig.7 Simulation result of XΦZ

如图6（a）所示，绿色粗线为设置的模拟真实面型的函数 M(y)，而蓝色细线为用三次样条插值算法处理后得到的面形值YMX，是模拟测量的面形值。可以从中看出，测量值的面型YMX基本与设计出的真实面型值函数相拟合。图6（b）是测量的面型值的误差。本文模拟的X向的行程为±0.2m，重复测量了5次，可以从中看出面型最大的误差在1.68×10-10m，而且越靠近量程的中心处，误差就会越小。

图7是旋转面型XΦZ的仿真结果。可以计算出XΦZ最大的误差是1.06×10-6rad，基本在快靠近程的中心处取得最大的补偿量，计算出XΦZ的标准差为7.49×10-7rad。

综上分析，本文设计的干涉仪反射镜面型校准方法可以有效地算出干涉仪的面型值，而且算出的面型值与实际的面型值的拟合度较高，YMX最大的误差在1.68×10-10m左右；XΦZ最大误差的值是1.06×10-6rad，标准差为7.49×10-7rad，该校准方法满足相应的技术指标。

4 结束语

本文设计了激光干涉仪测量位移系统反射镜的面型值计算方法。通过对激光干涉仪位移测量系统的测量原理的分析，设计出了对干涉仪反射镜面型值计算方法，并通过MATLAB仿真计算出了该方法测量X向反射镜在±0.2m量程的YMX面形值的最大误差为1.68×10-10m，XΦZ最大误差的值是1.06×10-6rad，该方法可以为实际的工程设计提供参考价值。