基于Shapley值的PPP项目客观因素超额收益分配
2020-03-26王亚磊罗瑜萱
王亚磊,罗瑜萱
(江西理工大学经济管理学院)
1 引言
目前所有相关研究都是将超额收益分配统一考虑,统一分配,这样是不对的。所以,基于委托代理理论,可以将超额收益分成两个部分,第一个部分就是投资者努力而产生的超额收益,第二种就是市场因素产生的超额收益,也就是说项目的固有生产能力。
现在假设g为高速公路的固有生产能力,也就是投资者不需要努力即可达到的水平,πr表示实际收益。πe为合理收益上限,这个上限是根据社会基准收益率去确定的;a表示投资者的运营能力,投资者运营能力越强,那么产生的收益越大。θ表示一个随机变量。
①当g>πe时,也就是说项目的固有收益大于合理收益上限。那么,这个时候就要去分类讨论,即第一部分超额收益是g-πe,由项目的固有生产能力而产生。就是说高速公路建好了,就会产生的收益,并不需要投资者去努力,去运营。第二部分收益是πr-g,这部分收益完全是由投资者努力而产生的超额收益。如果投资者不去努力,不去运营,那么就不会产生收益,所以,政府鼓励投资者努力创新,会激励投资者努力,而产生超额收益。
(2)当 g ≤ πe时,且 a+g+θ<πe,说明没有产生超额收益,那么进入合理收益分配阶段,这里不用讨论。当a+g+θ≥πe,那么这个时候,所有的超额收益都是由投资者努力而产生的。由于投资者努力而产生的超额收益相关研究比较多,所以这里不去讨论,对于客观因素产生的超额收益,相对研究比较少。
2 基于Shapley值得超额收益分配机制
在博弈论中,有合作博弈论和非合作博弈论,显然多于PPP高速公路项目,是政府部门和各投资者之间合作而产生的。政府部门提供特许经营政策和融资担保,而投资者提供资金以及强大的运营能力。故只有合作才能共赢。故在这种思路下引入合作博弈理论中的Shapley值,正是解决超额收益分配中客观因素产生的收益的有效途径,主要因为主管
因素产生的超额收益遵从激励相容约束,
运用委托代理理论更为合适。
2.1 Shapley值的思想
Shapley的核心目的就是在一个群体中,对于不同的方式参与项目S,以及每个个体对项目的贡献程度v,而去得出一个收益分配比例。其基本的思想就是各个参与者所获得的收益就是他对这个合作体所做出贡献的期望值。
2.2 Shapley值的值步骤
①验证合作博弈为实质博弈,在集合(N,v)上如果存在v(N)>∑v(i)且i∈N.也就是说合作的收益是大于不合作的收益。②超可加性—旧的联盟有组成新的联盟的动机,若R,S为参与项目S的个体,N为所有参与项目S的各个个体的集合,且,则v(R∪S)≧v(R)+v(S).③个体理性与集体理性
而且Shapley值最重要的假设前提是系统各成员的投入是均等的;故博弈(N,v)的Shapley值将大联盟的利益v(N)按照下述公式进行分摊:

其中N代表大联盟,v代表收益函数。参与者可以组成任意的小联盟S。w(S)表示概率,总和为1。V(s)为不同的小联盟S的边际收益,即参与者加入系统而带来的收益。Xi(v)对于联盟中的参与者i的利益分配函数。s表示联盟S中的参与人个数,v(β) =0。
3 加权得Shapley超额收益分配机制
虽然Shapley值PPP高速公路项目的超额收益分配上有很多优势,但是由于分配方案受到收益状况的影响,并未考虑风险因素、客户因素、努力因素、投入因素等的差异;由于风险共担,收益共享是ppp项目超额收益分配的核心原则,所以忽略了参与者之间的相互作用;在这里运用加权的Shapley值,将影响超额收益分配的因素考虑进去,考虑权重,使得收益分配更加合理。
其基本思路是①将对利益分配有影响的投入指标设为Cj,j=1,2,3,……,k。②利用定量分析方法求得各种指标 Cj下投入权重,λk,∑ λk=1.显然,各成员的各种投入为Cik,各成员i的投入Di= ∑Cik.可求得,各成员i实际承担的投入因子 D’i=Di/∑ Di,∑ D’i=1.实际投入因子与理论均摊因子1/n的差值:③利润分配补偿值:αi其中为调节系数,并且0<αi<1。最后,求得考虑投入因素时,应分利益为:
4 实例分析
本项目是栗镇石洋至鸡冠山三珑公路,他全长85km,投资额大概14亿元,包含了7个新建的工程,其中有两个投资者参与了项目,分别是A.山河建设集团,B.国龙投资集团。还有政府部门C。由于技术水平的差异,三方都做过相关调研,当C独立去做得话,产生的超额收益是2.161亿元,而A独立去做是3.455亿元,而B独立去做是4.455亿元。当C和A合作的话,产生的超额收益是8.522亿。当C和B合作的话是7.511亿元,而当A和B合作的话是6.451亿元。而当三方合作时,产生得超额收益为11.233亿元。
4.1 基于Shapley值的超额收益分配值得计算(见表1)
由此可以解得当三方合作时:
φA(V)=1.152+0.333+1.060+1.241=3.7 86亿元
同理φB(V)=1.512+0.499+0.898+0.904=3.813亿元
φC(V)=3.634亿元。
4.2 超额收益分配的调整
先根据项目的实际情况,对于影响上栗县公路工程项目超额收益分配的影响因素进行识别,总结出主要影响因素包括风险分担,以及投入因素,努力因素等建立ahp指标模型,这三个指标的权重分别为a1=0.354和a2=0.415,a3=0.231,K=0.1(见表2)
故由此得到的修正的超额收益分配值是:
φA(V)=3.786+0.1×11.233×(0.499-1/3)=3.972亿元
φB(V)=3.813+0.1×11.233×(0.247-1/3)=3.716亿元
φC(V)=3.634+0.1×11.233×(0.254-1/3)=3.545亿元
5 结语
在PPP高速公路项目中,收益分配一直是各方关注的重点和难点,其中超额收益分配更为重要,关乎着项目的成败,本文根据超额收益产生的原因,对于客观因素产生的超额收益,运用shapley值法对超额收益进行分配,同时基于风险分担,以及投入因素,努力因素对超额收益分配比例进行调整,使之更为合理。
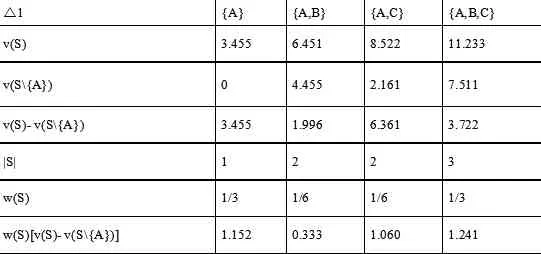
表1 基于Shapley值超额收益分配值

表2 上栗县公路项目超额收益分配影响因素
