一类p-Laplacian方程径向对称解的存在性

姚紫嫣,梁载涛,段 炼

(安徽理工大学数学与大数据学院, 中国 淮南 232001)

众所周知，p-Laplacian方程是一类特殊的椭圆型方程，是Laplacian方程的推广。近几十年来，该类方程在物理、生物及数学等领域得到了广泛应用，逐渐成为国内外学者研究的热点问题，当前处理该类问题的方法主要有单调迭代理论[1]、变分法[2]、不动点定理[3]等。近些年，p-Laplacian方程Dirichlet问题受到了学者们的关注，该类问题产生于非牛顿流体理论和多孔介质气体的湍流理论[4,5]，具体见文献[6-10]。

本文继续研究此类问题，我们考虑如下Dirichlet问题

(1)

径向对称解的存在性，其中p>1，B={x∈RN:|x|<1,N≥2}且f:[0,∞)→[0,∞)。

根据径向对称解u(x)=v(r)，其中r=|x|>0，问题(1)可转化为如下问题

(2)

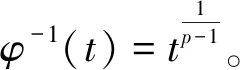
在文献[6]中，Wang等人研究了n维p-Laplacian系统的Dirichlet问题。而本文研究一维p-Laplacian方程Dirichlet问题，显而易见，当n=1时，有如下结果。

定理1若f0=∞且f∞=0，则问题(1)存在一个正径向解。其中

经过对上述结果进行分析，发现其条件较强，受其启发，我们将给出相对较弱的条件。基于锥不动点定理[11]，得到了如下结果。

定理2假设f满足下列条件之一：

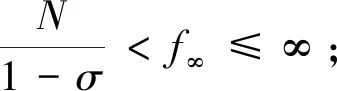
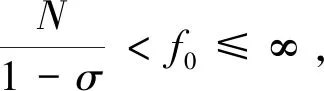
本文其余部分结构如下，第1节，主要介绍本文所需预备知识；第2节，主要对定理2进行证明；第3节，举例加以验证。

1 预备知识

如引言所示，本文主要结果的证明基于锥不动点定理，以下先简单介绍一下锥的定义和所需的引理。

若一个连续算子从有界集映射到一个相对紧集上，则它是一个连续紧算子。因此，若G是X中的子集，则定义GK=G∩K且∂KG=(∂G)∩K。

定义1设X为Banach空间，K是X中的非空闭子集，若K满足：

(d1) 对任意m,n∈K，a,b>0，有am+bn∈K；

(d2) 若m,-m∈K，则m=0，

则称K为X中的一个锥。

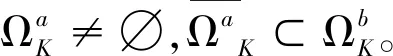
(A1) ‖Tv‖≤‖v‖，这里v∈∂KΩa；

(A2) 存在g∈K(〗0}使得v≠Tv+μg，其中，任意v∈∂KΩb且任意μ>0，

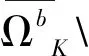
上述方法已被用于研究二阶微分方程正周期解[12]和Monge-Ampére方程径向解[13]问题。

引理2[14]对于任意的函数ω∈C[0,1]，满足ω(r)≥0，且ω′(r)在[0,1]上是递减的，则有

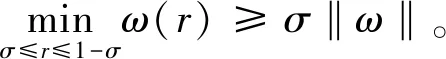
设

(3)

在证明主要结果之前，需回顾下列结果。

引理3[15,16]在(3)中定义的 Ωγ和Bγ具有下列性质：

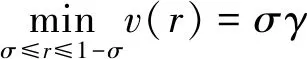
(h4) 若v∈∂KΩγ，则σγ≤v(r)≤γ，σ≤r≤1-σ。

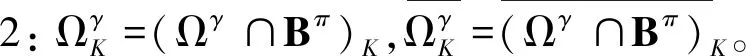
2 定理2的证明

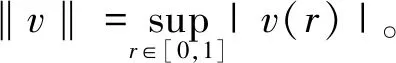
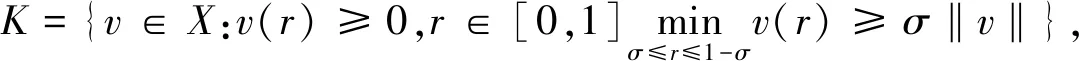
(4)

容易验证，K为X中的锥。

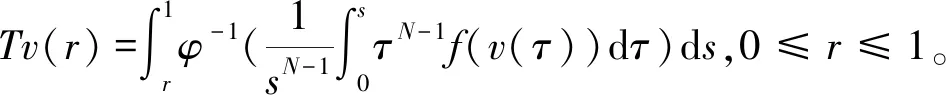
为了证明定理2，先给出并证明如下更一般的情形。

引理4假设下列两个条件成立：

(H3) 存在常数α>0,N>0和一个连续非递减函数φ:[0,∞)→[0,∞)使得

f(v)≤Nφ(α),0≤v≤α;

(H4) 存在常数β>0,N>0和一个连续非递减函数φ:[0,∞)→[0,∞)使得

那么下列两个结果成立：

(C1) 若α<σβ，则问题(2)至少存在一个正解v(r)使得

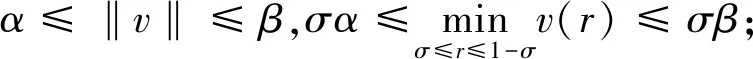
(C2) 若α>β，则问题(2)至少存在一个正解v(r)使得

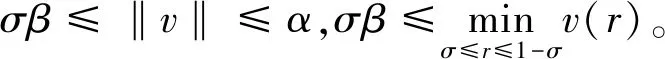
证明由引理1可知，需证明

(A1) ‖Tv‖≤‖v‖，这里v∈∂KBα，

(A2) 存在e∈K(〗0}使得v≠Tv+μe，这里v∈∂KΩβ且任意μ>0。

首先证明(A1)。由(H3)可知，对于任意v∈∂KBα且s∈[0,1]，有

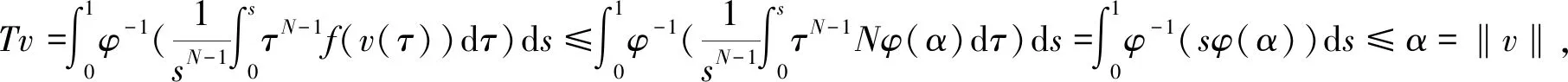
再证明(A2)。设e(r)≡1∈K(〗0}，需证明v≠Tv+μ,∀v∈∂KΩβ,μ>0。利用反证法。如若上式不成立，则存在v0∈∂KΩβ和μ0>0，使得v0=Tv0+μ0。由于v0∈∂KΩβ，则由引理3的(h4)，可得σβ=σ‖v0‖≤v0(r)≤β,σ≤r≤1-σ。由(H4)可知，

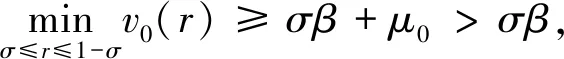
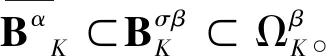
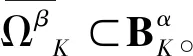
定理2的证明只需验证(H1)成立的情况，(H2)的验证与其类似。

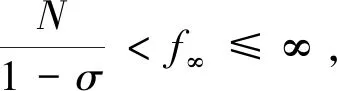
3 举例

为了验证主要结果的正确性，给出如下例子。

例子考虑下列Dirichlet问题

(5)

结论：当l>p-2时，问题(5)至少存在一个非平凡径向对称解。

证明若l>p-2，通过计算可得

因此，由定理2可知，问题(5)至少存在一个非平凡径向对称解。