深水锚泊主动式截断试验执行机构运动前馈控制
2020-03-26乔东生孙玉博马刚汤威闫俊欧进萍
乔东生, 孙玉博, 马刚, 汤威, 闫俊, 欧进萍
(1.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024; 2.哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001)
我国深海油气资源储量丰富,为提高深海油气开采技术水平,在深水平台及其锚泊系统设计中均需要进行物理模型试验,以验证其可靠性。然而,受现有水池水深的限制,无法按常规缩尺比直接模拟上千米水深的深水平台锚泊系统,所以Stansberc等[1]提出了将深水平台的锚泊系统截断以进行物理模型试验,称作截断模型试验方法(或混合模型试验)。截断锚泊系统上部是物理模型,而下部用数学模型代替,目前有被动式截断与主动式截断2种方法。被动式截断试验的实施过程是将截断点锚固在水池底部,以截断系统与全水深系统的静力和部分动力特性相似作为优化目标进行设计,最后通过数值重构和数值外推方法预报浮式平台系统的动态响应[2]。虽然被动式截断能够满足截断系统与全水深系统的静力和部分动力相似,但是仍存在2个主要问题:不能完全满足锚泊系统动力特性相似而使得无法直接利用物理模型试验结果准确预报运动响应;截断比例较小时被动式截断试验难于设计与实施[3]。主动式截断试验的实施过程是在水池底部布置执行机构,利用执行机构带动截断点按照真实的响应实现实时运动。为使截断点按真实的响应运动,需将其连接在执行机构上以实时跟踪输入的运动信号,而其中的关键问题是如何选择并控制执行机构实现截断点实时高精度的运动跟踪目标。高文军[4]使用并联式六自由度执行机构——Stewart平台来模拟截断点的运动,基于SolidWorks建立了执行机构的模型并通过Motion插件进行运动模拟,但是仅模拟了执行机构的机械运动,未考虑执行机构从接受信号到实现响应驱动的时滞等问题,但该研究表明了采用Stewart平台搭建主动式截断的执行结构具备一定可行性。同时,Stewart平台的性能优于其他六自由度的串联机构[5]且用途多样,因此本文同样选择Stewart平台作为执行机构,并基于运动学原理与控制算法研究其在主动式截断试验中的实施过程。刘晓昕[6]叙述了Stewart平台的运动学和动力学反解推导过程并利用Matlab编写了计算工具箱。张尚盈等[7]使用牛顿法推导了Stewart平台的运动学正解,结果显示该方法可以快速得到精确的位姿结果。Thomas等[2]证明了时滞会严重影响主动式截断试验的精度。另外,主动式截断试验要求执行机构能够实时精确地跟踪运动信号,所以应选择合适的控制方法来提高执行机构运动的跟踪精度与速度。Stewart平台的控制主要分为:工作空间控制[5,8-9]、铰点空间控制[10-11]。单腿驱动电机控制一般是通过运动学反解计算每个电机腿所需完成的伸缩量从而完成Stewart平台的整体位姿控制,并没有考虑摩擦、外部荷载、时变性等因素,而当这些因素较强时会导致Stewart平台难以达到期望的位姿,即使驱动电机的动态特性优良,Stewart平台的整体运动跟踪效果仍可能很差。整体动力控制通过考虑Stewart平台的动力学模型,计算出驱动电机所需出力大小从而实现对上平台位姿的精确控制,但这样做的代价是计算耗时并难以实现实时控制。驱动电机的控制性能主要反应在其动态特性、鲁棒性、抗干扰性。因此,只需要让单个电机具有良好的控制性能,这样外界干扰在可控范围内时就无需进行复杂的动力控制。已有研究表明前馈控制能够极大地提高系统的响应速度,张士涛等[12]指出:前馈控制需要受控对象的精确建模消除其零极点来实现高精度跟踪控制;在低频输入时前馈控制的幅值增益近似为1,相移几乎为0,这就说明前馈控制能够让受控对象精确地跟踪输入信号。Lee等[13]利用递推最小二乘法辨识电液驱动电机模型,使用PID控制提高鲁棒性与抗干扰性,并设计了基于模型的零相差跟踪控制提高系统响应速度。此外,截断点执行机构需要提供的锚泊线张力相当于驱动电机的负载扰动,而负载扰动会让驱动电机存在跟踪误差。王福超等[14]使用干扰观测器与零相差跟踪控制补偿了外部扰动并显著提高了响应速度。李志军等[15]利用系统名义模型设计了干扰观测器补偿负载扰动并提高系统抗干扰能力,使得电机在受到负载扰动后可以快速恢复到应有运动状态并消除负载扰动对系统跟踪精度的影响。
本文使用Matlab/Simulink建立Stewart平台的运动学模型,以永磁同步电机(PMSM)为例对Stewart平台驱动电机进行系统辨识,然后根据辨识得到的传递函数G01(s)设计前馈控制算法和干扰观测器,最后将运动学模型、电机模型、控制算法三者集成仿真,验证前馈控制对执行机构运动跟踪的控制效果。
1 执行机构运动学模型
1.1 选择执行机构
根据主动式截断试验的特点,本文选择Stewart平台作为执行机构,如图1所示,其具有如下优点:
1)具有6个运动自由度,不仅可以完成深水平台截断锚泊系统试验,还可以用于未来的其他试验用途,如船模试验等;
2)因为深水波浪周期一般较大,所以其响应时间能够满足采样定理;
3)运动学推导简单,若已知上平台的角度和中点坐标则可以通过矢量叠加推导出6个支腿的端点坐标与长度;
4)控制方法简单,因为6个支腿的驱动电机(或液压系统)是相同的,所以只需要研究单个支腿的模型即可进行高精度的位姿控制;
5)结构对称、刚度高、不易损坏。
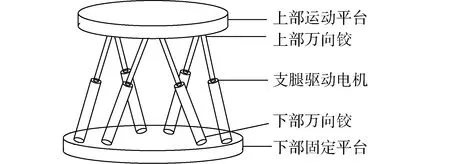
图1 Stewart平台Fig.1 Stewart platform
1.2 Stewart平台运动学原理及其Simulink模型
Stewart平台的电机支腿与平台之间通过万向铰相连,6个支腿运动通过电机进行驱动。Stewart平台运动学可分为正解与反解2个过程,正解即利用6个支腿的长度求解上部运动平台位姿(中点坐标与平台角度),反解即在已知上部运动平台位姿时求解6个支腿长度(或驱动电机的伸缩量)。
输入位姿信号后,通过反解可获知平台6个支腿所需达到的长度,与实际长度比较后获得驱动电机伸缩量并驱动支腿运动,驱动完成后通过正解可以计算平台达到的实际位姿。如果实际位姿与输入位姿有误差则需要设计控制算法以提高精度。基于Matlab/Simulink建立Stewart平台的运动模型从左到右共3大模块:反解模块、6支腿驱动电机与控制算法模块、正解模块,如图2所示。为了验证3大模块是否准确,首先假设6个支腿都能够实时精确地跟踪输入信号,且在迭代过程中引入低通滤波器来提高数值计算的稳定性。在Stewart平台可达范围内输入位姿信号为X=150sin(2πt) mm,计算得到的位姿跟踪误差如图3所示,表明了建立的运动学模型能够正确运行。

图2 Stewart平台的Simulink模型Fig.2 Simulink model of Stewart platform

图3 Stewart平台位姿跟踪误差Fig.3 Position tracking error of the Stewart platform
2 Stewart平台控制策略
假设6个支腿的驱动电机完全相同,选择铰点空间控制方法建立控制策略如图4所示,包含执行机构运动学模型,驱动电机模型建立、基于驱动电机模型的前馈控制和干扰观测器设计。3个部分的模型进行集成仿真,验证针对驱动电机设计的控制算法对Stewart平台运动跟踪控制的有效性。
2.1 驱动电机系统辨识
1)辨识对象
因为永磁同步电机(permanent magnet synchronous motor,PMSM)动态响应好,应用范围广,所以本文选择PMSM作为Stewart平台驱动电机进行系统辨识与控制算法设计,采用的电机参数如表1所示。假设纯时滞相对于系统的惯性可以忽略,基于Matlab/Simulink建立PMSM模型,如图5所示。PMSM的反馈控制方法为电压空间矢量控制结合电流环PI控制[16-17],电机的阶跃响应如图6所示。阶跃响应稳定在输入信号±2%误差之内所用时间为调节时间Ts,反映系统的响应速度,根据Simulink计算结果Ts=15.45 ms。
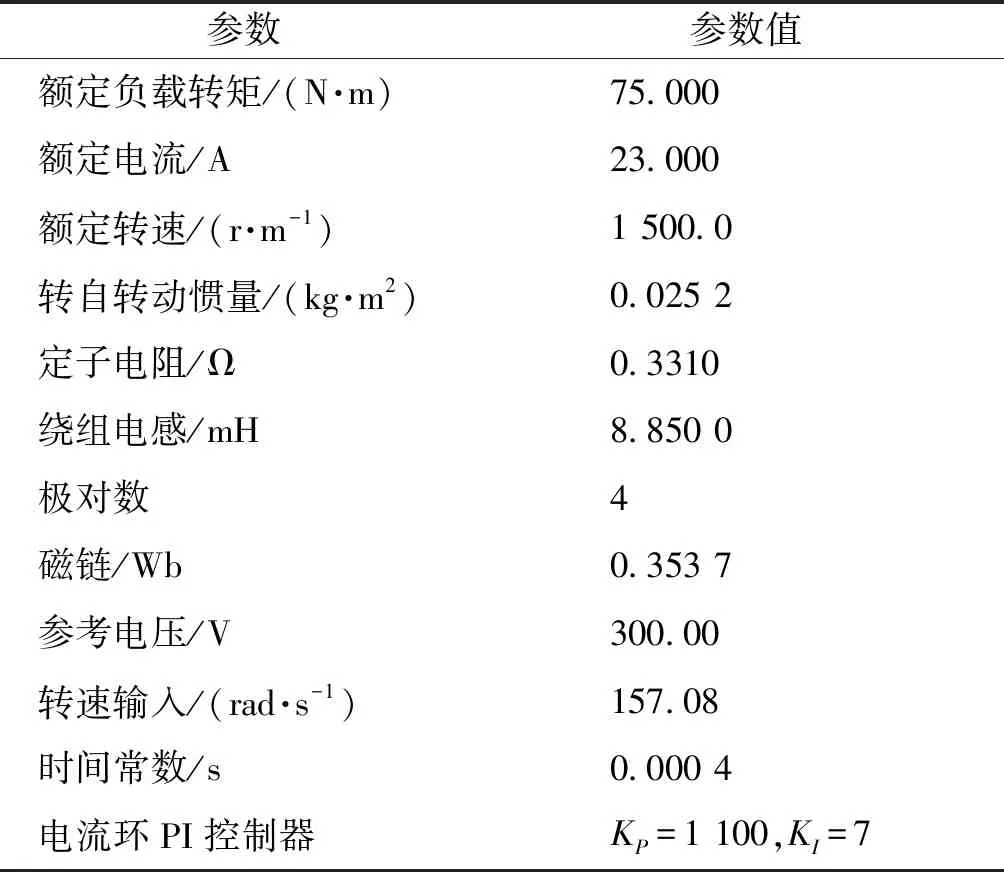
表1 PMSM参数表Table 1 Parameters of the PMSM
2)传递函数系统辨识
使用白噪声信号对PMSM模型进行测试并采集实际转速输出数据,使用Matlab的系统辨识工具箱进行辨识。具体的辨识输入信号:采样时间为2 ms,方差为25π的白噪声信号。经过对比不同结构传递函数的辨识精度,选择结构辨识精度最高,达到94.7%。

图4 Stewart平台控制策略Fig.4 Control scheme of Stewart platform

图5 PMSM的Simulink模型Fig.5 Simulink model of PMSM

图6 PMSM阶跃响应Fig.6 Step response of PMSM
(1)
式中:a0、a1、a2、b0为待辨识参数;s为微分算子。G01(s)与原模型对白噪声的跟踪效果如图7所示。

图7 G01(s)与原模型白噪声信号跟踪效果对比Fig.7 White noise signal tracking comparison between G01(s) and original model
2.2 前馈控制
1)前馈控制传递函数
在高性能伺服控制中,前馈控制可用来提高系统的响应特性和跟踪性能,且前馈控制的设计只与受控对象有关。设受控对象辨识模型如式(1),则前馈控制为:
(2)
因为前馈控制F01(s)的分母阶数大于分子阶数,这样在物理上是无法实现的,可以用F01(s)乘上一个低通滤波器使得分母阶数大于等于分子阶数,滤波器的形式:
(3)
其中:取时间常数τ=0.001,滤波器阶数i=2。则:
(4)
综合式(1)~(4)代入得到前馈控制传递函数:
(5)
在受控对象与输入信号之间引入前馈控制后,原模型阶跃响应的调节时间由15.45 ms减小到9.94 ms,稳态跟踪误差为0.4%,如图8所示。此外,当输入为白噪声信号时,在前馈控制的作用下原模型稳定在±2%误差之内所需的调节时间更短,即可以更快地跟踪白噪声信号,如图9所示。

图8 前馈控制下的系统阶跃响应Fig.8 System step response under feed-forward control
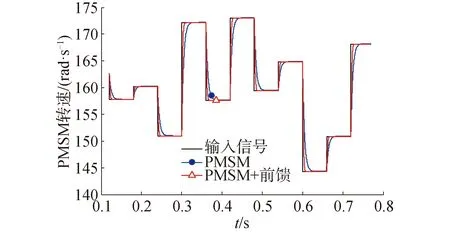
图9 前馈控制下系统对白噪声信号跟踪效果Fig.9 Signal tracking effect of white noise under feed-forward control
2.3 干扰观测器
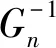
(7)
式中:Q是低通滤波器,同式(3);Gn为系统辨识模型;G是系统实际模型。当Gn与G近似相等时,式(7)简化为H(s)=G,即引入扰动观测器后,驱动电机能有效地抵抗负载扰动,快速地消除跟踪误差,并不影响系统其他部分的控制算法设计[14-15]。
当系统在0.05 s时施加75 N·m的阶跃负载扰动,计算仿真结果如图10所示。原模型在负载扰动影响下无法精确地跟踪输入信号,存在26%的跟踪误差;引入干扰观测器后,系统在扰动下仅产生了7.6%的跟踪误差,且系统能在0.01 s内将跟踪误差恢复到2%以内;当系统有前馈控制时,虽然干扰观测器会让系统产10%的超调量,但是对稳态跟踪误差和响应速度没有影响,因此不会影响前馈控制的设计。系统在75 N·m的负载下对白噪声信号的跟踪效果如图11所示,可见干扰观测器和前馈控制的共同作用提高了PMSM的响应速度与抗干扰性。
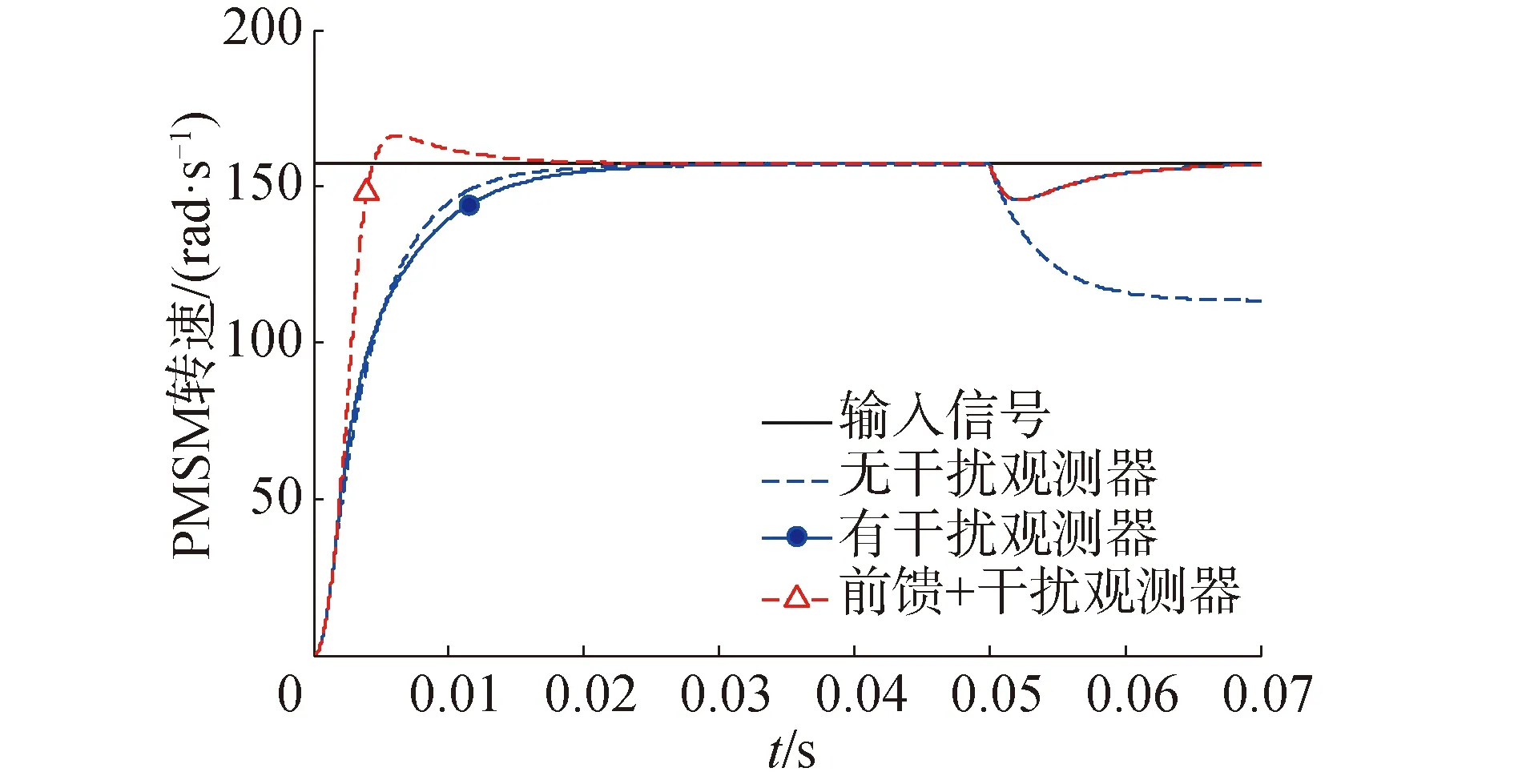
图10 阶跃信号跟踪效果Fig.10 Step signal tracking effect
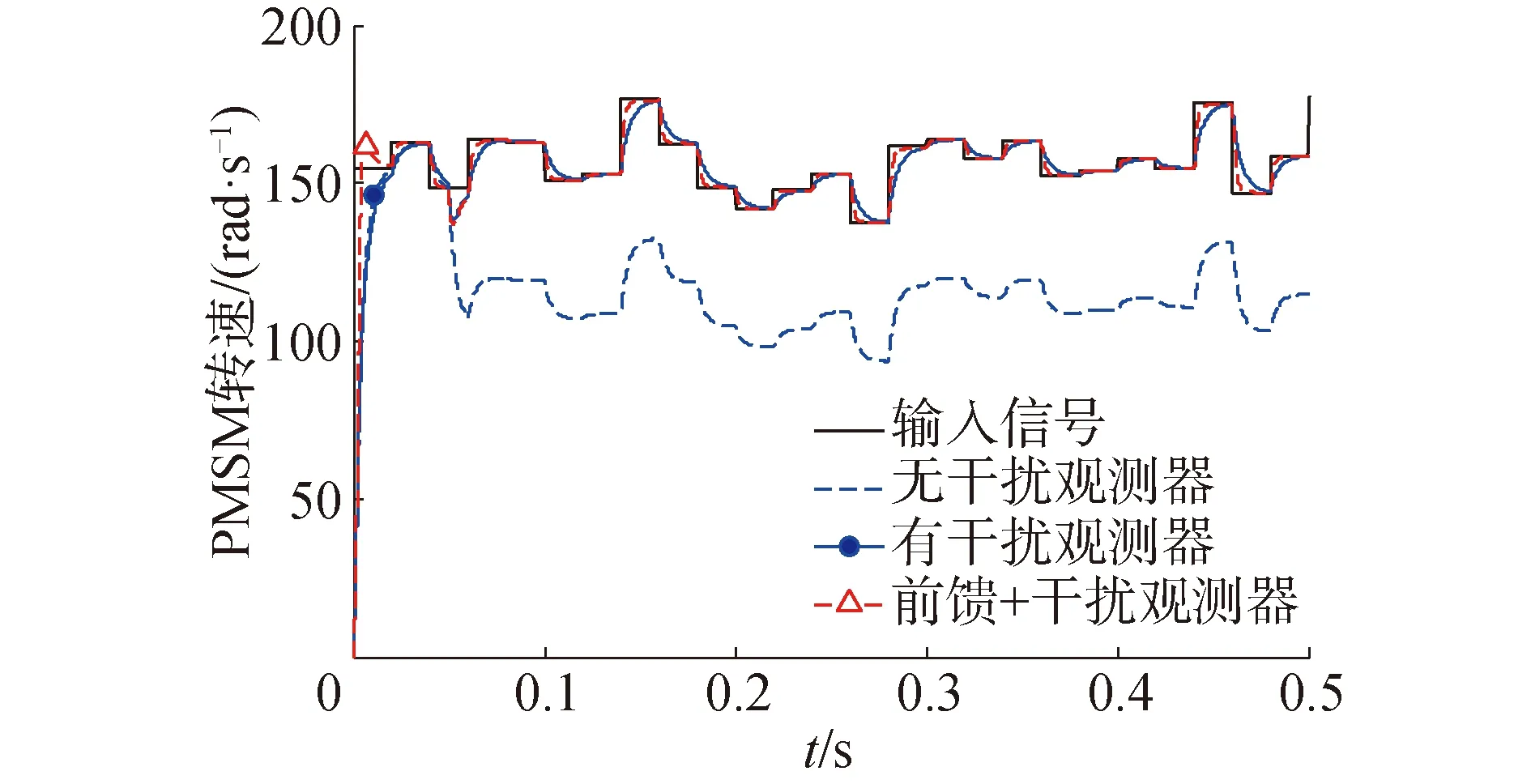
图11 白噪声信号跟踪效果Fig.11 White noise signal tracking effect
3 Stewart平台位姿跟踪控制仿真
根据上文建立的Stewart平台六自由度运动学模型,将第2节得到的驱动电机辨识模型和前馈控制集成到6支腿模块,图12所示。模拟驱动电机与前馈控制对Stewart平台运动跟踪性能的影响,并验证前馈对Stewart平台的控制效果。

图12 2种集成仿真模型Fig.12 Two integrated models for simulation
3.1 阶跃信号测试
将驱动电机传递函数模型与前馈控制集成到Stewart平台运动模型,输入位姿信号为幅值60 mm的X方向阶跃信号,阶跃响应如图13所示。根据Simulink计算结果,无前馈控制、引入前馈控制2种模型下X方向阶跃响应的调节时间分别为57 ms和31 ms,前馈控制使调节时间减少了46%。

图13 Stewart平台X方向阶跃响应Fig.13 Step response to X direction of the Stewart platform
3.2 正弦运动信号跟踪测试
无前馈控制、引入前馈控制2种模型对正弦位姿输入信号X=150sin(2πt) mm的运动跟踪误差如图14所示,有前馈时跟踪误差幅值约为无前馈时的50%。综上,将6支腿驱动电机模型及前馈控制引入运动模型后,前馈控制能有效提高Stewart平台的运动跟踪速度与精度。
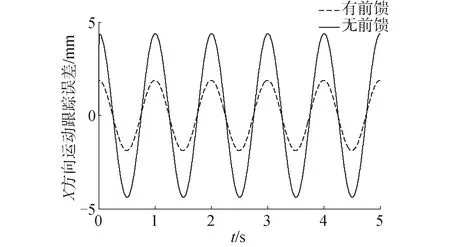
图14 Stewart平台正弦位姿跟踪误差Fig.14 Tracking error of the Stewart platform under sine position
4 结论
1) 前馈控制能有效地提高系统响应速度。引入前馈控制后,PMSM模型阶跃响应调节时间从15.45 ms减小到9.94 ms,且PMSM能够更快地跟踪白噪声输入信号。
2) 干扰观测器可以有效地消除负载扰动对系统跟踪精度的影响。无干扰观测器时,受干扰系统跟踪误差为26%且无法恢复到±2%以内;引入干扰观测器后,系统跟踪误差最大为7.6%且能够在0.01 s内恢复到±2%以内。此外,干扰观测器不会影响前馈控制的设计与控制效果。
3) 辨识得到的驱动电机传递函数可以用于前馈控制与干扰观测器的设计,且2种控制方法共同作用能够有效提高驱动电机的响应速度与抗干扰性,从而使得Stewart平台更适用于需要实时性和快速性主动式截断试验。
4) 将运动学模型、电机模型与控制算法进行集成仿真,无前馈时Stewart平台的单方向位姿跟踪速度为57 ms,引入前馈后提高到31 ms,可见针对单腿驱动电机设计的控制算法能有效提高Stewart平台的响应速度。
