某型电动微型汽车转向梯形的优化设计

2020-03-26杨丽蓉

科学技术创新 2020年1期

杨丽蓉

（西华大学，四川成都610039）

当汽车行驶时，无论直行或转向,都要保证车轮与路面作纯滚动,减小甚至避免前轮的侧滑,以减小行车的摩擦阻力,减少轮外胎磨损及摩擦生热,延长轮胎的寿命,因此提高汽车转弯时的稳定性是相当重要的[1]。同时,也能减少对路面的破坏而延长公路的使用寿命。正确设计转向梯形机构，可以保证汽车转弯行驶时，全部车轮绕瞬时转向中心旋转。

1 设计目的

作为该微型电动车转向系的一个部分，转向器的主要功能就是保证汽车时按照驾驶员的意志而向某个方向转动，实现车辆偏转。本文对转向梯形机构的优化设计进行了研究，以汽车内外轮作纯滚动的Ackerman 运动学为基础, 对汽车梯形转向机构优化设计进行分析，得到转向梯形臂的优化长度以及梯形底角，用前后车轮轴距L、前轮两轮之间的距离B 和汽车最小转弯半径Rmin, 得到车辆内外轮转角曲线[2]。

2 设计过程

2.1 已知参数

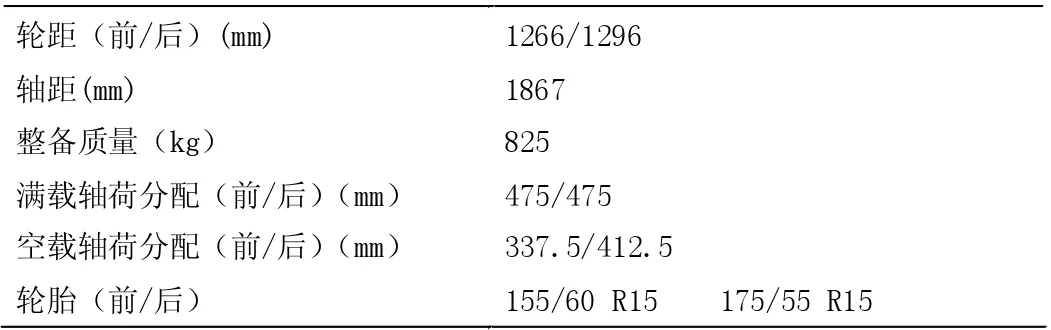
表1 车辆已知参数

2.2 转向盘及转向轮内外最大转角的确定

汽车转向盘应汽车转向运动完成后，具有自主保持直线行驶的能力。根据《汽车设计》知不同汽车方向盘的直径D 如表2所示[3]。

表2 不同汽车方向盘直径

考虑到整车的机动性，当转向轮达到最大转角时，此时车辆的最小转弯半径为轴距的2～2.5 倍。该车轴距为1867mm，其半径为（2～2.5）×1867mm=(3.7～4.7)mm,尽量取小值保证良好的机动性，故取Rmin=4m。

如图1 所示，设β 为内轮转角，α 为外轮转角，L 为汽车轴距。

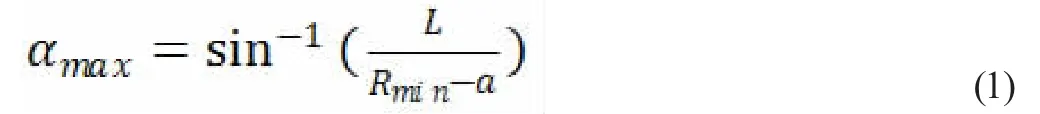
式中α 为主销偏移距。其值在（0.4～0.6）倍轮胎胎面宽度，即a=（0.4～0.6）×155=(62～93)mm,故取a=77mm。

根据式（1）可得转向轮外轮最大转角

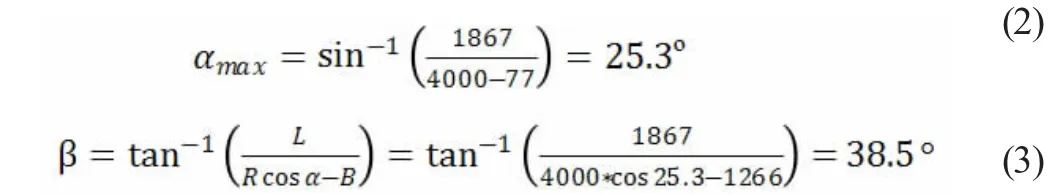
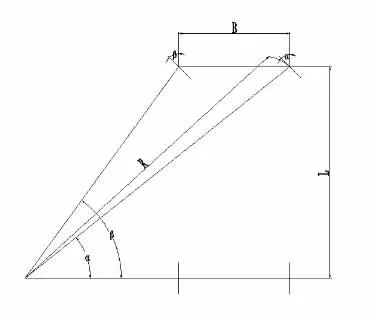
图1 转角关系图

2.3 阿克曼转向梯形

汽车转向行驶时会弹性轮胎侧偏角的影响，所有车轮是绕位于前轴和后轴之间的汽车内侧某一点滚动。此点位置与前轮和后轮的侧偏角大小有关。由于影响轮胎侧偏角的因素很多，并且很难精确确定，故下面是在忽略侧偏角的影响下，分析该汽车的转向问题。此时，两转向前轮轴线的延长线应交在后轴延长线上，如图2 所示。设分别为内、外转向轮的转角，L为轴距，K 为两主销中心线延长线到地面交点之间的距离[4]。若要保证全部车轮绕一个瞬时中心行驶，则梯形机构应保证内、外轮转角应满足式（4）：

阿克曼梯形即为满足阿克曼转向理论特性的四连杆机构，其底角γ（见图3）可由下式（5）确定：

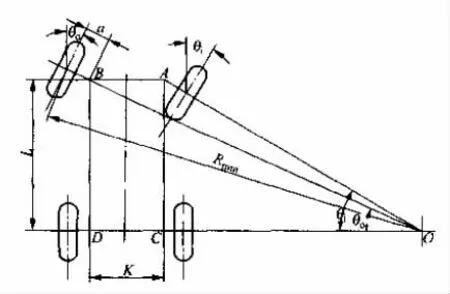
图2 理想的内、外轮转角关系图

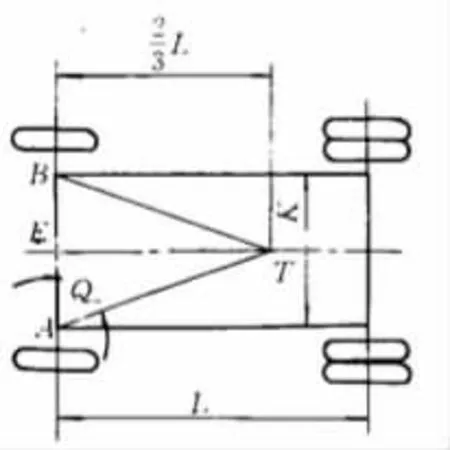
图3 底角γ

其梯形臂的作用长度m=(0.11K～0.15K)；

阿克曼梯形是一个如图4 所示的平面梯形，其特性为：（1）；（2）梯形上底长度AB 与两主销中心距及两主销中心线穿地点完全一致。

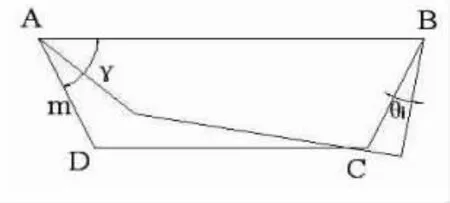
图4 阿克曼梯形

3 优化设计及结果

3.1 外轮解析式

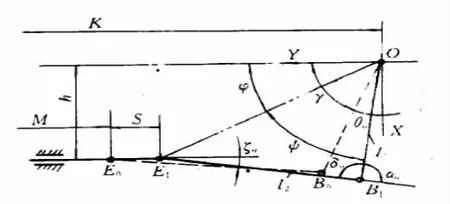
图5 外轮一侧杆系运动情况

取梯形底角顶点O 为坐标原点，X、Y 轴方向如图5 所示，则可导出转向横拉杆l2表达式，齿条行程S 与外轮转角的关系：

对于故障代码“U101300 控制单元未编码”，需对“44-动力转向”进行手动编码。对“44动力转向”执行“控制单元自诊断>访问权限”时的登录码为10608。对“44-动力转向”执行“控制单元自诊断>编码”时，进行手动编码004F。上述操作可通过ODIS诊断系统也可借助ODIS-E工程师软件来完成，不必在线。

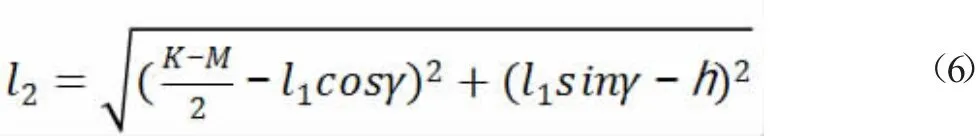
由图中几何关系可得到：

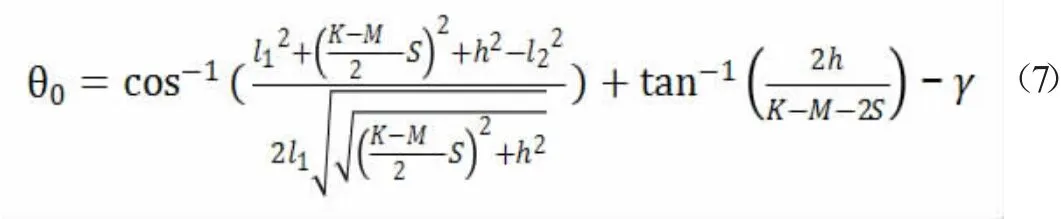
3.2 内轮解析式

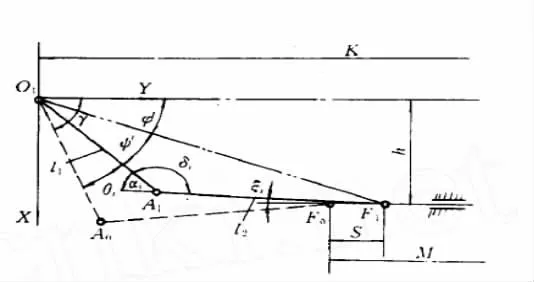
图6 内轮一侧杆系运动情况

由图6 可知：

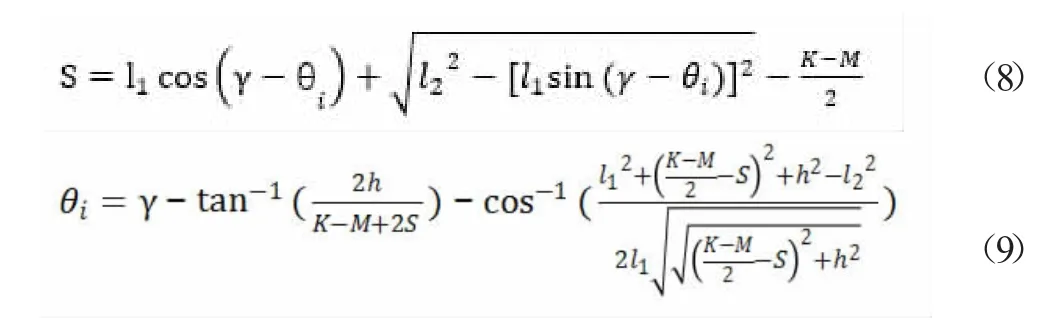
因此，利用上面的公式可得出函数：

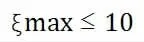
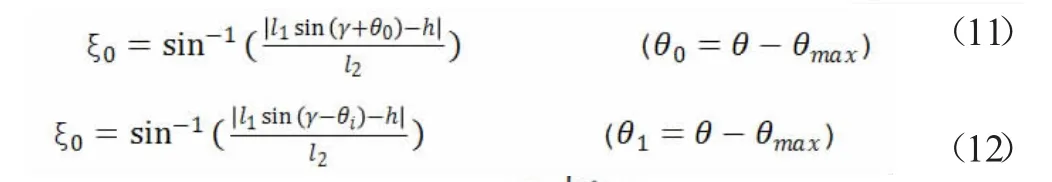
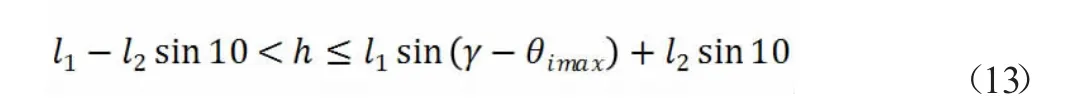
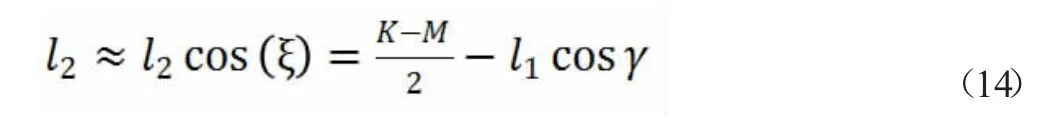
分析可知上述不等式可简化为

由此可确定出h 的取值范围。

再结合优化目标函数可得到优化方法，使优化目标转角误差最小，即

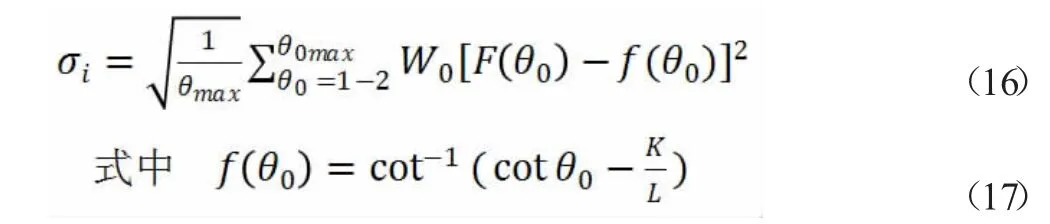
W0为加权因子，因为在不同转角所用到的频率各不相同，故要设定一个加权因子。

本次设计运用Visual Basic 6.0 对断开式转向梯形机构进行优化编程。优化后得到最佳底角γ=650；梯形臂长度m=100mm；转向横拉杆长度l2=319.327mm，在本次设计中，取得横拉杆长度l2=320mm。优化结果如下图7。

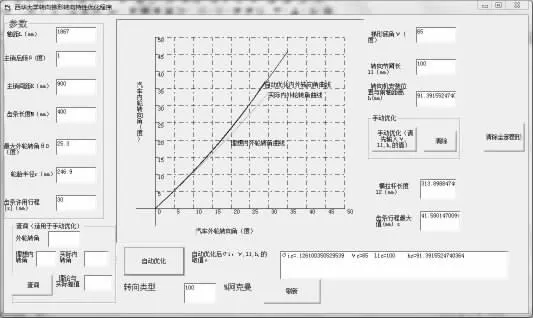
图7 转向梯形优化结果

结果分析说明：（1）从优化结果可以看出来，应用本次所建立的目标函数以及约束条件进行求解与车辆实际值很接近，说明本次采用的数学模型是正确的。（2）从图7 可以看出，在自变角很小的范围内，实际转角和期望转角随自变角的变化曲线基本上重合，，但随着自变角的增大，它们之间的误差也越来越大。由于在自变角小于20?的范围内是常用的转角角度，所以本次优化是合适的。