基于陷波器的永磁电机振荡抑制

毕京斌，贾智军，孔宴伟，夏 猛

(1.中车青岛四方车辆研究所有限公司, 青岛 266112； 2.中国铁路成都局集团有限公司成都动车段, 成都 610000)

0 引 言

永磁系统能够准确跟踪或复现输入指令，凭借其良好的动态响应性能、高的准确性和稳定性，在各行各业中得到了广泛应用[1]。近年来，随着科学技术的快速发展，数控机床的精确定位，导弹武器的精确制导，零件器件的精密加工以及大功率设备的拖动等各个领域，都对永磁系统提出了更高更严格的指标要求。有关永磁控制研究热点的主要方面有：低速爬行问题、振荡抑制问题、快速精确定位、减速再起动等。这些都是永磁精确控制的关键问题，想进一步提高永磁系统的性能，就必须解决以上问题，本课题主要针对永磁控制中的振荡抑制问题进行研究。系统的稳定性是系统工作的前提，机械谐振导致永磁统在谐振频率处不稳定，为了保证系统的稳定性，应使谐振频率在闭环带宽以外，即需严格控制系统的带宽。机械谐振不仅限制了系统闭环带宽，也限制永磁系统的控制器增益，导致动态性能下降，降低了系统的控制精度[2-3]。机械谐振导致系统不稳定，设备发生强烈振动产生噪音的同时也对机械部件造成磨损，大大缩短了设备使用时间。机械谐振还会使永磁电机产热增加，造成不必要的能源损耗。由此可见，机械谐振的危害极大，在投入使用前必须对其进行有效抑制。

如果系统长时间工作在振荡状态下，会对机械系统中的联轴节、传动齿轮、传动轴、轴承等零件造成严重损伤，特别针对中高压大功率电机驱动系统，如果谐振抑制不当产生断轴等事故，后果十分严重。对于数控机床、激光加工设备等加工精度要求较高的应用场合，机械谐振会对产品的加工质量造成严重影响，无法满足生产要求。为了提高永磁驱动系统带宽、快速减小阶跃响应的偏差，需要提高控制环路的增益，而机械谐振的存在限制了控制环路增益的提高。机械振荡还会发出噪声，在其工作环境中产生噪声污染。

谐振频率是影响永磁系统稳定性和控制性能非常重要的参数，对永磁系统的闭环带宽、动态性能以及稳定性都有很大影响，所以机械谐振的抑制对于保证系统性能尤为重要。抑制机械谐振首先要检测出系统的谐振点的位置，在测得系统的谐振频率点之后再加入相应的控制环节的方法加以抑制，因此，如何快速准确得检测谐振频率点变得尤为关键，对后续的谐振抑制也有重要指导意义。随着对永磁系统机械谐振研究的不断深入，在谐振频率检测方面也取得了较大进展。根据谐波检测的发展历程，已经存在了几种检测方法[4-5]：基于模拟滤波器进行谐波检测；基于傅里叶变换的谐波测量方法[6-8]；基于小波变换方法的谐波测量[9]；基于神经网络的检测方法[10]。为抑制检测到的谐振频率，文献[11]采用数字陷波滤波器来抑制机械谐振，但是这种陷波器的在中心频率点的陷波幅值很大，会对系统性能造成较大影响，此外陷波幅值和宽度由同一参数控制，不容易调节。文献[12]在传统的陷波器的基础上，经过扩展提出了一种改进的陷波器。通过参数的适当设置使陷波中心频率点衰减的幅值与谐振引起的幅值大体抵消，在抑制谐振的同时尽量提高系统的动态性能。

在实际永磁系统中，谐振频率点的位置及其幅值受外界环境变化、负载惯量变化和以及系统自身特性变化的影响，经常会发生变化，采用传统的滤波器具有很大的局限性。永磁系统的谐振频率点的偏移通常会导致陷波滤波器抑制谐振的失效，因此又有人提出了自适应陷波器的方法。自适应陷波器能够实时监测系统谐振频率的变化，并根据谐振频率点的变化修正滤波器参数达到机械谐振抑制的目的，弥补了传统陷波器的不足。文献[13,14]提出了一种自适应陷波器，将其加入控制器中在一定程度上抑制了永磁系统的机械谐振。文献[15]提出了一种谐波检测和传统陷波滤波器相结合构成自适应陷波器进行在线抑制谐振的方法。

本论文主要研究使用陷波滤波器抑制机械谐振。针对实际系统中发生的机械谐振，需要研究运行过程中在线自动辨识其谐振特征的方法，并根据谐振辨识出的谐振情况，自动配置陷波滤波器参数，实现自动抑制机械谐振的目的。

1 永磁电机控制振荡系统模型搭建

1.1 交流永磁电机数学模型

交流永磁同永磁电机的数学模型比直流电机要复杂的多，为了便于分析，在建立数学模型之前，做了如下假设：

(1)忽略磁滞损耗的影响。(2)不考虑铁心饱和。(3)不计涡流损耗。(4)转子上无阻尼绕组。(5)永磁材料的电导率为零。

交流永磁永磁电机在A-B-C坐标系上的电压方程为

(1)

式中，ua、ub、uc为三相定子相电压的瞬时值，ia、ib、ic为三相定子相电压的瞬时值，Rs为定子电阻，ψa、ψb、ψc为定子相绕组磁链瞬时值。

以矩阵形式表示电压方程，可得：

(2)

式中，p为微分算子。永磁体磁链的幅值为ψf，其在三相绕组中可以表示为

(3)

式中，ψra、ψrb、ψrc为转子相绕组磁链瞬时值，θ为永磁体磁链与定子绕组夹角。定子磁链方程为

(4)

电磁转矩方程为

(5)

式中，Te为电磁转矩，np为电机极对数。

1.2 双惯量振荡系统数学模型

双惯量系统又称为双质量系统，在工业应用中十分常见，如工业机器人、轧钢机等，一般由永磁电机、被驱动负载以及连接二者的传动轴等组成，双惯性系统模型如图1所示。

图1 双质量系统模型

图中，JM、JL、Ks分别为永磁电机的惯性矩、负载端的惯性矩和传动轴的弹性系数、Tm、Tl、ωm、ωl分别为电机转矩、扰动转矩、电机转速和负载转速。该系统的传递函数G(s)为

(6)

其中，Jall=JM+JL，wp为共振频率，wz为反共振频率，表达式如式(7)和式(8)：

(7)

(8)

从公式可看出，双惯性系统的共振频率和反共振频率是由电机和负载端的转动惯量以及轴的刚度产生。当负载端转动惯量很大时共振频率约等于反共振频率，当电机和负载转动惯量固定时，系统共振频率只与轴的刚度有关，轴刚度为

(9)

式中，r0为轴半径，G为剪切模量，L为轴的长度。

根据图1可知，双惯性系统的状态方程：

(10)

式中，Ts为连接永磁电机与被驱动负载的轴的转矩，BL、BM为负载和电机的粘滞系数。

2 基于陷波器的共振抑制方法设计

陷波中心频率，陷波宽度以及陷波深度是影响陷波滤波器的3个重要参数。陷波中心频率是指需要滤除的频率点，深度参数是指陷波滤波器在中心频率处提供的幅值衰减，宽度参数则是陷波器幅值衰减到-3dB时前后两个频率点的差值。合理设置陷波滤波器中心频率，深度参数和宽度参数可以很好地对永磁系统的机械谐振进行补偿。

2.1 陷波器原理

对于一个存在机械谐振的永磁系统，可以通过向系统控制中加入陷波滤波器减小谐振频率点处的幅值以达到谐振补偿的目的。抑制方法的基本原理如图2所示。可以看出通过合理设计陷波器的参数，将谐振频率点处的幅值大致抵消，最后使系统频率响应趋近平滑，达到谐振抑制目的。

图2 基于陷波器的动态谐振抑制原理框图

陷波器是无限冲击响应(IIR)数字滤波器，该滤波器可以用以下常系数线性差分方程表示：

(11)

式中,x(n)和y(n)分别为输人和输出信号序列，ai和bi为滤波器系数。对式(11)两边进行z变换，得到数字滤波器的传递函数为

(12)

式中,zi和pi分别为传递函数的零点和极点。

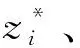
这样零点、极点配置的滤波器称为单一频率陷波器，在频率ω0(ω0为要消除的频率)处出现凹陷。而把极点设置在零的的径向上距圆点的距离为l-μ处，陷波器的传递函数为

(13)

式中,μ越小，极点越靠近单位圆，则频率响应曲线凹陷越深，凹陷的宽度也越窄。当需要消除窄带干扰而不能对其他频率有衰减时，陷波器是一种去除窄带干扰的理想数字滤波器。

2.2 陷波器设计

实际永磁系统大都是采用向控制系统中加入滤波器的方法来进行谐振补偿。陷波器可有效地滤除信号中谐振成分，陷波器的传递函数：

(14)

式中，f为陷波中心频率，Hz；ξ为深度参数，表征了中心频率处幅频特性的深度，在中心频率处可提供-20lgξdB的幅值衰减；k为宽度参数，Hz，表示以陷波中心频率为中心幅值下降3dB时的两侧宽度；通过调整滤波器的ξ，k两个参数，可以得到不同陷波幅值和带宽的频率特性，两个参数的整定原则:

(1)当0<ξ<1时，且宽度参数k不变时，其频率特性曲线是凹陷的，且当ξ越小时陷波中心频率处提供的幅值衰减越大，如图3所示。

(2)当深度参数ξ固定不变时，随着宽度参数 值的增加，频率特性曲线凹口的范围逐渐大，如图4所示。

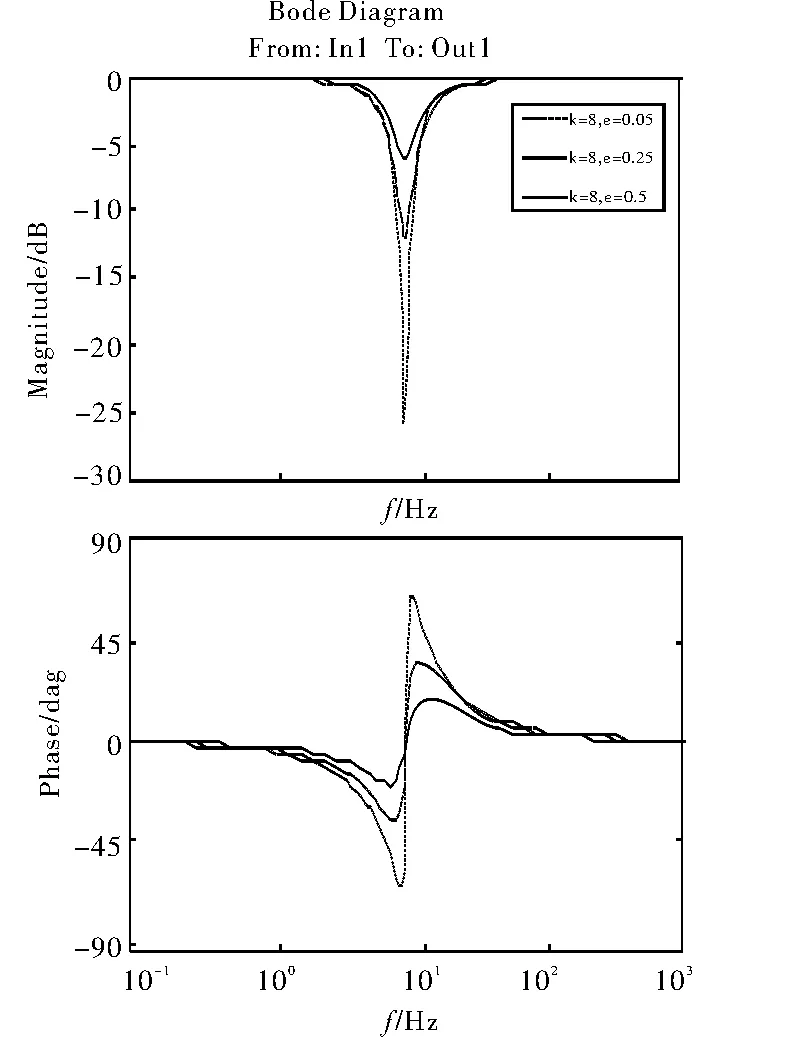
图3 不同ξ下陷波器幅相频率特性曲线

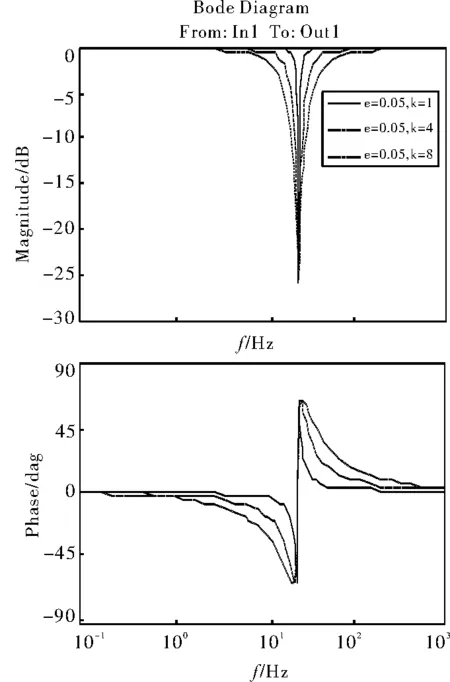
图4 不同k下陷波器幅相频率特性曲线

图3和图4为参数整定原则的效果图。图3是在中心频率f=10Hz，宽度参数k=8时，深度参数分别为x=0.5、x=0.25、x=0.05时的陷波滤波器的频率特性曲线。可以看出随着深度参数的减小，中心频率处衰减的幅值逐渐增加。图4是在中心频率f=10Hz，深度参数x=0.05时，宽度参数分别为k=1、k=4、k=8时的陷波滤波器的频率特性曲线。随着宽度参数k值的增加，频率特性曲线凹口的范围逐渐增大。从两个图中也可以看出陷波滤波器的宽度参数和深度参数可以单独调节，这就克服了传统形式的滤波器只能通过调节一个参数完成深度和宽度调节存在的问题。

2.3 陷波器主要参数对陷波效果的影响探究

为了验证陷波器的正确性，模拟了一个幅度为1，频率为10kHz的正弦波，其中掺杂着幅度为1，频率为20kHz的正弦噪声，用Matlab设计一个20kHz的陷波器，将掺杂了20kHz噪音的10kHz信号经过滤波器，利用FDATool导出Matlab程序验证陷波器的正确性并导出陷波器系数，其滤波器前后的波形及放大波形如图5所示。

从上面的正确性验证波形可知，陷波器的理论设计及仿真设计都是可行的，在永磁振荡系统中，同样需要陷波器对谐振频率进行抑制，消除闭环系统中的谐振信号，达到谐振消除的目的。由表1可知，仅改变apass参数由小变大，调节时间依次减小，但是对应的滤波范围变宽，“点”阻效果变差。由表2知，仅改变bw参数，带宽越大，虽然抑制越快，但窄带会变宽，即可滤频率增多，单一性差。

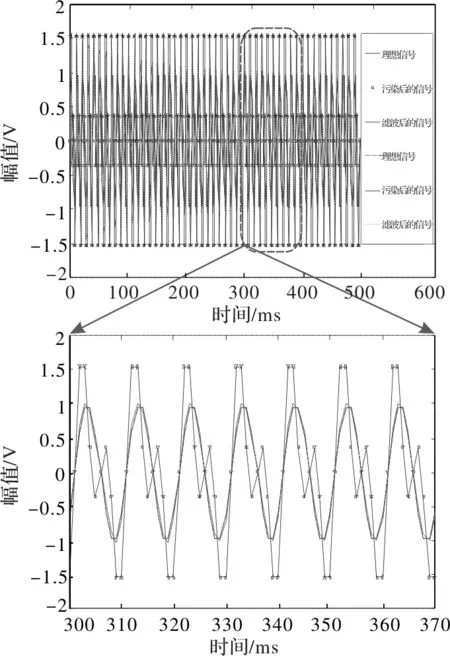
图5 20kHz陷波器陷波前后效果对比波形

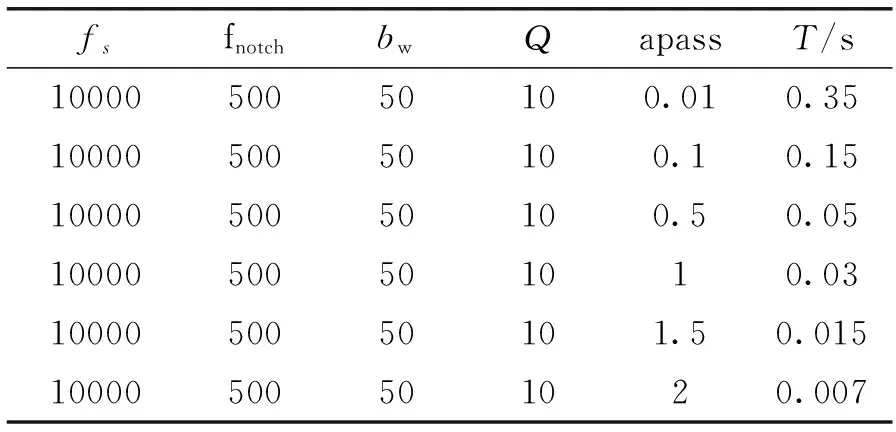
表1 陷波器apass参数对陷波效果的影响

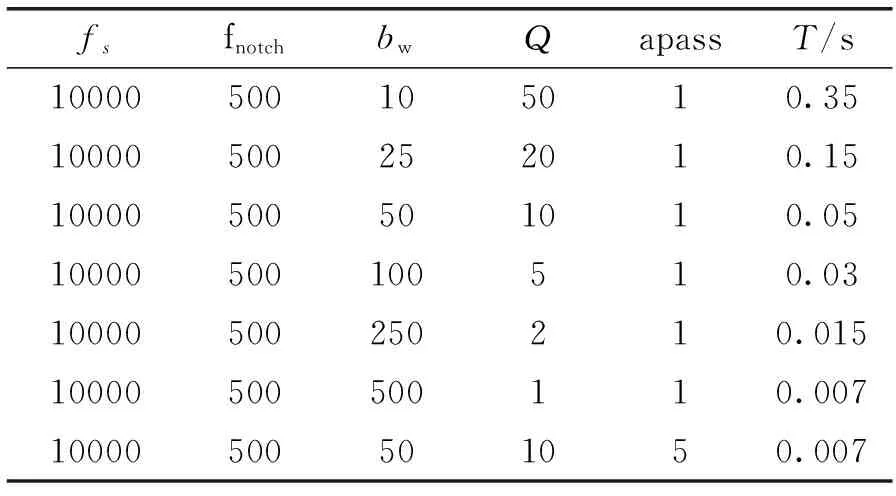
表2 陷波器bw参数对陷波效果的影响

研究证明了陷波器参数需要寻优，即参数apass和bw之间需要折中值以满足系统静动态响应。

3 实验验证

永磁同步电机参数：额定功率PN=2kW，额定线电压UN=380V，额定电流IN=7.5A，定子电阻Rs=0.1Ω，直轴电感Ld=2430mH，交轴电感Lq=2430mH，转动惯量J=0.23kg·m2，额定负载TL=7.5N·m，极对数p=2，额定转速nN=2500r/min。

在上一节陷波器理论设计部分已经对陷波器本身进行了正确性验证，可实现特定频率的消除，并分析和验证了陷波器不同参数对陷波效果的影响规律，基于以上研究，寻优了一组合适的参数设计陷波器，将其应用于永磁定位振荡抑制系统中。由末端振荡引起的谐波频率一般在100～1000Hz之间，属于中频范围。针对500Hz振荡频率，引入频率为500Hz，幅值为10V的正弦干扰，加在速度环的反馈回路上，陷波器设计参数如下：采样频率fs=10000Hz，陷波频率fnotch=500Hz，带宽bw=400，通带apass=15。导出陷波器系数后，经双线性变换得到S域的传涵，将其置于速度环与电流环之间，首先仿真验证了双闭环情况下，陷波器对500Hz谐波的抑制，有效减小了转速稳态误差，如图6所示。

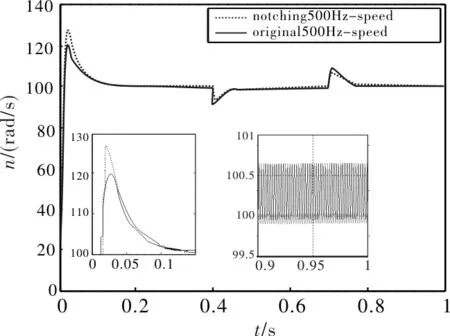
图6 500Hz陷波器对转速的影响

图6中给定转速为100rad/s，转速的上升时间为0.04s，由于陷波器的影响，在放大图中可见超调了28rad/s，即超调量由20%上升到了28%。在0.4s和0.7s之间加了50%额定负载，经过陷波器滤波后的系统能快速跟随转速响应，可满足快速性要求。在0.9s时转速稳态误差明显减小，由原来的0.6rad/s减小到了0.1rad/s，转速振荡得到了抑制。

同理，针对300Hz振荡频率，引入频率为300Hz，幅值为10V的正弦干扰，相应的陷波器设计参数如下：采样频率fs=10000Hz，陷波频率fnotch=300Hz，带宽bw=200，通带apass=15。仿真验证了3环情况下，陷波器对300Hz谐波的抑制，有效减小了转速稳态误差，如图7所示。

图7 300Hz陷波器对位置的影响

由图7可知，在300Hz谐振干扰的系统中，给定位置信号50rad，在2s和4s之间加了50%额定负载，经过陷波器滤波后的系统能快速跟随位置响应，可满足快速性要求。速度环速度稳定在20rad/s，转速稳态误差明显减小，由原来的2rad/s减小到了0.3rad/s，转速振荡得到了有效抑制。同时对A相电流滤波前后进行了FFT分析。

图8 300Hz陷波信号FFT分析

如图8所示。由图8可知，陷波前300Hz频率含量很高，达到了基频的160%，经过陷波器滤波后，300Hz频率含有量减小为20%，有效抑制了振荡频率。

4 结 语

本论文主要研究使用陷波滤波器抑制机械谐振。针对实际系统中发生的机械谐振，需要研究运行过程中在线自动辨识其谐振特征的方法，并根据谐振辨识出的谐振情况，自动配置陷波滤波器参数，实现自动抑制机械谐振的目的。为了验证效果，设计一个可以改变谐振频率的实验平台，并在平台上验证谐振抑制效果。首先，详细分析交流永磁永磁电机的数学模型、矢量控制系统的基本思路。其次，建立谐振模型，并推导谐振频率表达式，通过理论分析得出引起永磁系统机械谐振原因。进而针对在线谐振抑制问题，采用陷波滤波器消除机械谐振的设计方法，设计数字化陷波器，研究滤陷波器的谐振抑制效果。最终对基于陷波器的永磁定位末端振荡检测及抑制进行了验证。