动态路径规划形式化集成建模方法

曹 凯，奉 柳，刘秉政，沈 鹏，杨 旭

(山东理工大学 交通与车辆工程学院，山东 淄博 255049)

静态环境中机器人的路径规划问题主要解决以下3个问题：确定机器人出发的初始点和到达的目标点；规划机器人从初始点到达目标点同时躲避静止障碍物的轨迹；控制机器人追踪轨迹到达目标点。然而，动态环境中的路径规划问题会更加复杂，它需要面对移动的障碍物不断地评估和调整规划方案，以适应新的环境动态变化，这种动态环境中的路径规划方法对于机器人的开发才更有实用价值。

已有很多种动态环境路径规划方法被广泛应用，常用的包括人工势场法、粒子群法、概率路线图方法以及一些改进的启发式方法等。其中，人工势场法通过创建势能地形，并利用势能梯度下降进行导航和局部规划。该方法结构简单、执行时间短，便于底层实时控制，广泛应用于动态环境中多机器人问题。例如，多无人机避碰问题[1-2]、足球机器人路径规划问题[3-4]和移动机器人[5-8]等等。但是，其在路径寻优过程中还存在着可能陷入布局最优的局限性。为此，本文提出将形式化随机可达集建模方法与人工势场法相结合，在机器人与多个移动障碍物之间建立Ad-Hoc网络，提供机器人与移动障碍物之间的相对动态关系更加准确的表达方式和安全评估方法，从而提高动态环境中机器人避障路径规划的成功率。

随机可达性分析通过在有限时间内评估系统状态是否保持在状态空间的期望子集内，或者躲避状态空间的不期望子集来判断系统状态的安全性，为动态系统的安全验证提供了一种有效方法。然而，随机可达集的计算复杂度随系统状态维度增加呈指数级增长，因此利用其在动态环境中评估障碍物移动碰撞概率是不可行的。为此借鉴文献[9]提出采用离线计算在线查询的方法。然而，这种离线计算在线查询的方法对移动障碍物反应的灵敏度有限，因而易受到障碍物移动冲突的影响。

为此，本文利用随机可达集遍历系统动态的表现优势以及人工势场法在动态环境中局部规避较为灵活的特点，采用预先离线成对计算机器人与每个移动障碍物的随机可达集，并为每个障碍物构筑斥力场，然后在路径规划阶段在线查询。这里随机可达集的任务是提供机器人与移动障碍物之间碰撞概率的精确描述，而人工势场法依据斥力梯度提供机器人与障碍物碰撞的可能性。

实际上，在具有多个障碍物的动态环境中，由于是孤立地为每一个移动障碍物计算可达集，所以多个可达集的交集显然不能提供严格的安全保证。尽管存在这种限制，但是与其他Ad-Hoc法相比，由于是相对于机器人-障碍物动态计算随机可达集，因此随机可达集为碰撞概率与斥力场的关联提供了一种形式化方法。也就是说，可以使用Ad-Hoc方法生成可比较的斥力势场，然后将这种斥力势场与障碍物和机器人的相对运动联系起来。

1 基本假设

1.1 障碍物动态

为了提高计算随机可达集的时效性，本文采用降低维度的方法。为此，在所观察的动态环境中，假设移动障碍物具有如下特性：移动障碍物的速度具有随机性；移动障碍物遵循的轨迹为直线、弧线或由直线和弧线叠加的任意曲线。

(1)

而对于具有角速度w∈W和半径r∈R+的弧线运动，动态被离散化为

(2)

1.2 机器人-障碍物相对动态

(3)

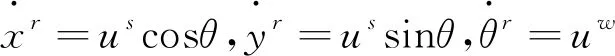
(4)

式中：us是速度；uw是独轮车的角速度。

用时间步长Δ离散化机器人动态式(3)的结果为

(5)

离散化机器人动态式(4)的结果为

(6)

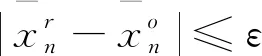
(7)

式中：fr(·)由式(5)和式(6)给出；fo(·)由式(1)和式(2)给出，那么碰撞可以定义为

(8)

1.3 随机可达集

(9)

(10)

Δfo(w,n))p(w)

Δfo(w,n))p(w)}

(11)

确定躲避碰撞的系统最优控制输入u。

(12)

式中Bi为对应于机器人避免与障碍物i碰撞的事件集合。因此，需要分别检查机器人与每个障碍物的避碰概率，并且取避碰概率的最小值为总体避碰概率的上界。虽然这个避碰概率上限不一定能完全保证安全，但它至少可以告知机器人哪条路径更可能躲避碰撞。由于本文的目的是在众多可选路径中找到一条具有更高成功率的到达目的地路径，而不是从理论上保证无冲突路径，因此上限式(12)是适合的。

2 算法集成

为了将随机可达集与人工势场法集成使用，需要利用随机可达集生成障碍物梯度和引向目标的梯度。为此必须先改进随机可达集以适应人工势场法，即将随机可达集合并到梯度计算中，然后更新机器人的控制律。

使用随机可达集来预示势场变化的一大难点是式(11)最优值可能存在非平滑点。一般来说，这种平滑性是难以保证的。这一点可以通过图1给出的验证结果来说明。该图验证的是在直线运动模式下，机器人-障碍物相对动态的随机可达集平滑性。验证从坐标原点开始，每图右面的彩色柱状图表明碰撞概率由小到大的变化程度。机器人动态分别采用了1.2节中考虑的两类机器人模型，即完整质点模型和非完整独轮车模型。图1(a)和(c)表现的是高斯卷积平滑处理前，两类机器人模型的随机可达集不连续状态表现；图1(b)和(d)表现的是使用了参数为N(μ=0,σ2=0.152)的高斯卷积平滑处理后，两类机器人模型的随机可达集连续状态对比。由此可见，高斯卷积平滑处理在表现随机可达集连续状态的作用。

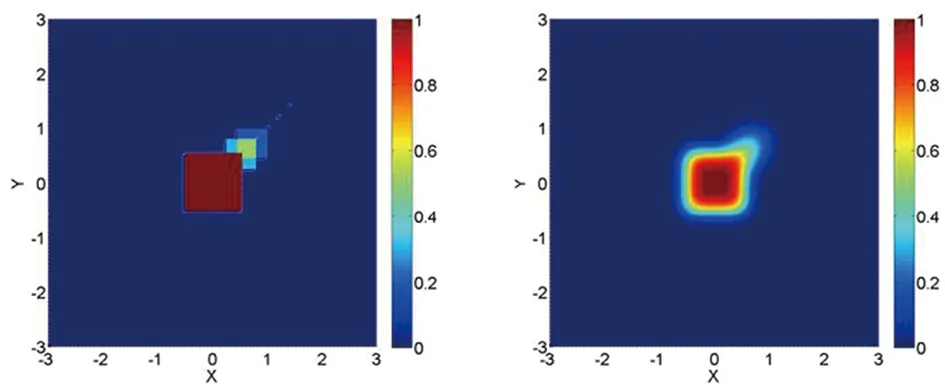
(a)不连续状态 (d)平滑处理后的连续状态

(c)不连续状态 (d)平滑处理后的连续状态图1 随机可达集平滑处理对比Fig.1 Comparison of random reachable sets smoothing

对于机器人附近的每个障碍物O，如果O在相对距离dmin范围内，则需要查询O对机器人的势场影响。要计算这个梯度，首先从距离机器人当前相对位置找到随机可达集中的最小邻近值pi,j；然后用以pi,j为中心的二阶中心有限差分计算这个梯度，再将每个障碍物的梯度合成在一起，生成所有障碍物最终共同的梯度。而函数goal-gradient是一个不断指向目标的梯度向量，将函数goal-gradient与每个障碍物的梯度合成获得最终的人工势场梯度，记为APFvector，如图2所示。

图2 障碍物梯度和合成势场梯度Fig.2 Obstacle gradient and synthetic potential field gradient

在算法1中，子函数U-O发挥了关键作用，即通过不断更新障碍物位置形成动态环境。为此，在算法2中将给出子函数U-O的具体计算过程，其中子函数U-O采用与计算随机可达集相同的动态方程，而且在每个采样时刻，算法2基于可能的速度分布p(w)来评估障碍物的速度w，并用该速度更新障碍物动态。

在获得APFvector之后，分别对两种系统模型利用函数calcControl(APFvector)计算控制输入u，即对于完整质点模型，有u=APFvector；对于非完整独轮车模型，从APFvector中提取航向和速度以便构建u=(us,uw)。为此，首先将uw设置为APFvector方向上的最大转弯率；然后将us设置为APFvector方向上的最大速度，这样独轮车的最大速度就与随机可达集计算中使用的最大速度相同；最后，使用u来更新机器人的控制律。

3 算法验证

为了演证本文提出的A-S算法对机器人避碰的路径引导中的效果，将A-S算法与具有参数N(0,σ=(0.15 )2)和N(0,σ=(0.45 )2)的高斯人工势场法[12]，依次进行噪声影响、完整质点模型和非完整独轮车模型的验证。

3.1 噪声影响验证

在现实动态环境中，机器人的环境感知经常面临许多不确定性。因此，实验中采用以障碍物的真实位置为中心的有界均匀分布，对每个时间步长感知到的障碍物位置进行随机抽样来模拟不确定性。其中均匀分布以障碍物宽度(1 m)的10%、25%和50%为界。例如，如果噪声被限定在50%范围内，并且障碍物的真实位置在原点，则该障碍物的感知位置可以在(0.5 m，0.5 m)、(-0.5 m，0.5 m)、(-0.5 m，-0.5m)以及(0.5 m，-0.5 m)的范围内的任何地方。

图3表示了在障碍物位置噪声存在的条件下，障碍物数量对成功率的影响。实际上，10%的噪声水平就意味着所感测到的障碍物位置可以根据均匀随机分布偏离真实位置，最大可达10%的障碍物宽度。

(a)A-S算法(b)σ = 0.15的高斯方法(c)σ = 0.45的高斯方法图3 噪声水平与障碍物数量对成功率影响的对比Fig.3 Comparison of the effects of different noise levels and number of obstacles

从图3(a)、(b)和(c)对比可知，对于所有噪声水平，A-S算法比高斯方法具有更高的成功率。验证可知，除了在拥有最大噪声量的高度拥挤情况下，A-S算法的成功率基本不受传感器不确定性的影响。

3.2 完整质点模型验证

如图4所示，在这个验证环境中，最大速度为0.36 m/s的完整质点模型机器人从起点车道位置S(-10 m，2.5 m)到目标位置G(15 m，7.5 m)，需跨越5条有移动障碍物的车道。动态障碍物在车道上行驶，并且利用障碍物动态式(1)对每个障碍物的速度进行随机采样。车道内障碍物运行的方向是从左向右和从右向左交替进行的，目的是增加对机器人向目标位置移动干扰的复杂度。为了保持障碍物的密度，障碍物在离开区域边界时被传送到其反向车道。

图4 多车道变道验证模型Fig.4 Verification model for lane changing in multi-lane

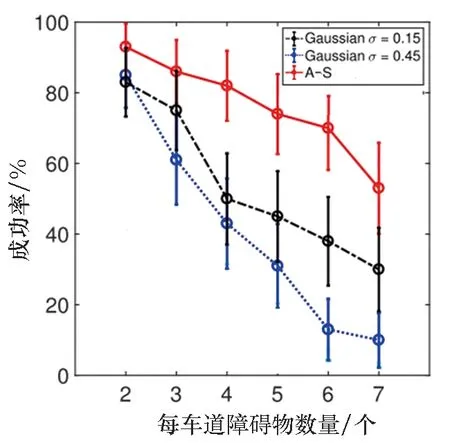
图5 算法成功率比较Fig.5 Comparison of success rates of three algorithm

图5展示A-S算法与其他方法成功率的比较，由于将形式化的随机可达集与Ad-Hoc 人工势场法集成，A-S算法提供了机器人-障碍物之间的相对动态更加准确的表达，从而提高了机器人对障碍物冲突反应的灵敏度，因此较其他方法有更高的成功率。

3.3 非完整独轮车模型验证

在这个实验中，采用非完整独轮车模型式(4)建模机器人动态，且从初始点S向目标点G行驶，而障碍物遵循随机方向的直线轨迹运行。实际上，在非完整约束条件下，如果不对路径进行修改，就无法用文献[9]中提出的离线计算随机可达集在线查询方法来求解这个问题。

图6(a)比较了A-S方法和高斯方法的成功率。由此图可以看到，与性能表现最好的高斯方法比较，A-S方法的成功率提高了约50%。这是由于随机可达集的引入，找到距离机器人当前相对位置的最小邻近值pi,j，再以pi,j为中心计算更为有效的躲避引导梯度，从而使得A-S方法能够做出更优指向目标的路径规划决策。

图6(b)展示了单次运行每种方法路径变化示例。期初在遇到移动障碍物较少时，三种方法的路径差异不大。由图6(b)的黑色圆部分可见，A-S方法与高斯方法在此处由于障碍物的冲突而产生背离运行，这种背离是由于用随机可达集所构造势场梯度的形状发挥的作用。另外，由于独轮车速度方向从正向负急剧变化，从而产生方向急剧反转，所以这些路径比完整机器人的路径更不稳定，因此机器人采取的是更激进的躲避方式来避开障碍物。由图6(b)最后路段三种方法比较可见，由于高斯方法在即将到达目标位之前与障碍物发生碰撞而停止不前，最后只有A-S方法躲过所有障碍物到达目标位。

图6(c)显示了所有方法与障碍物之间的斥力间隙的比较，由此表明无论环境如何变化，A-S方法的斥力势场的作用更加稳定，因而能产生更灵活多变的路径。

(a) A-S方法和高斯方法的成功率 (b)每种方法路径变化示例(c)不同方法与障碍物之间斥力间隙的比较图6 路径选择与成功率比较Fig.6 Comparison of path selection and success rate

4 结论

本文提出的形式化方法与Ad-Hoc方法集成具有如下优势：

1)形式化的随机可达集提供了碰撞概率的精确表示，其用于产生准确反映碰撞概率的势能梯度。

2)与高斯人工势场法比较，机器人面对移动障碍物的冲突的反应更加灵敏，不易被快速移动的障碍物所伏击。

3)该方法通过组合多个随机可达集来生成具有多个移动障碍物的近似避碰概率，从而容易表达和处理多移动障碍物的情况。

虽然研究结果表明提出的方法优于可比方法，但质点模型机器人是实际机器人的简化，尽管更符合实际的机器人模型可以集成到随机可达集的计算中，但需要更大的额外计算成本。另外，在实际应用中，离线计算的随机可达集数据库需要不断更新，才能适应范围动态变化的环境。