基于虚拟阵元冗余平均的对称嵌套MIMO雷达DOA估计

张宇乐, 胡国平, 周 豪, 朱明明, 赵飞龙

(1.空军工程大学防空反导学院， 西安， 710051； 2.93951部队， 青海格尔木， 816000)

MIMO雷达[1]具有良好的空间、频率、波形分集特性，能形成有效的大观测孔径，对增大虚拟阵元孔径[4]、优化检测和跟踪性能[5]、提高测向分辨力和精度[7]等具有重要意义，陆续有学者从DOA估计、多参数联合估计、非理想阵列条件下阵列参数估计等方面系统开展了MIMO雷达测向研究。传统MIMO雷达通常采用密布均匀线阵(Uniform Linear Array, ULA)作为发射和接收阵列进行DOA估计，其回波信号模型中的虚拟阵元个数受到物理阵元数限制，导致阵列的DOA估计性能受阵列孔径影响。嵌套阵[8](Nested Array, NA)的高自由度特征可以突破物理阵元个数的限制，有效提高阵列孔径，并且能得到确定的阵元位置和自由度闭式解。为提高嵌套阵虚拟阵元数，文献[9]建立了超级嵌套阵结构，该结构具有传统嵌套阵的所有优势，同时有效降低了阵元间互耦。文献[10]通过引入附加阵元建立了改进嵌套阵结构，自由度得到较大提升。上述算法仅仅利用了稀疏阵矢量化后形成的“差联合阵列”来扩展有效孔径，自由度扩展有限。MIMO雷达能够通过匹配滤波得到“和联合阵列”，实现虚拟孔径的扩展，将嵌套阵列与MIMO雷达体制结合，便可实现从“差联合阵列”到“和差联合阵列”的转变，从而进一步提升系统自由度。因此，将嵌套阵列与MIMO雷达体制结合起来开展多目标测向具有重要的理论意义和应用前景。

文献[11]采用二阶嵌套MIMO雷达，其发射和接收阵列均为二阶嵌套阵，增大了系统自由度，但其“和联合”阵列条件下的虚拟阵元存在不连续的问题，解决方法是选取连续的虚拟阵元进行DOA估计，但会损失掉离散虚拟阵元，自由度性能未得到充分利用。文献[12]通过设计发射和接收阵元间距，提出一种优化嵌套MIMO的无孔差合阵列，但其“和联合阵列”也不连续。文献[13]将嵌套子阵重新排在嵌套阵的两侧，提出了一种高自由度低复杂度的增强嵌套阵，并给出了实际阵元位置的4种形式。

综合考虑自由度、连续虚拟阵元等因素，本文提出一种对称嵌套阵结构，其发射阵列和接收阵列分别由2个以零点为参考中心布列的密布均匀线阵和稀疏均匀线阵组成，该阵列结构将传统虚拟阵元由“差联合”结构形式转化为对称“和联合”结构形式，形成的连续虚拟阵元数多，因此其可估计的目标数更多，角度估计性能更好，且接收阵元间距变大，互耦率更低，有助于提高测向精度。另外，针对现有算法都是删除“和差联合”阵列形成的重复虚拟阵元而丢失数据信息的问题，本文通过冗余平均处理后重构Toeplitz矩阵[14]，结合MUSIC算法实现DOA估计。该算法可以在不损失阵列有效孔径的条件下实现更多目标的DOA估计。

1 对称嵌套MIMO雷达系统模型

考虑单基地收发分置系统，对称嵌套MIMO雷达系统见图1，将2个均匀线阵以原点为中心对称布列，发射阵列由密布均匀线阵组成，共有Mt=4M-1个阵元，阵元间距为d；接收阵列由稀疏均匀线阵组成，共有Nr=2N-1个阵元，阵元间距为2Md，d为单位阵元间距，一般等于半波长λ/2，λ为信号波长。

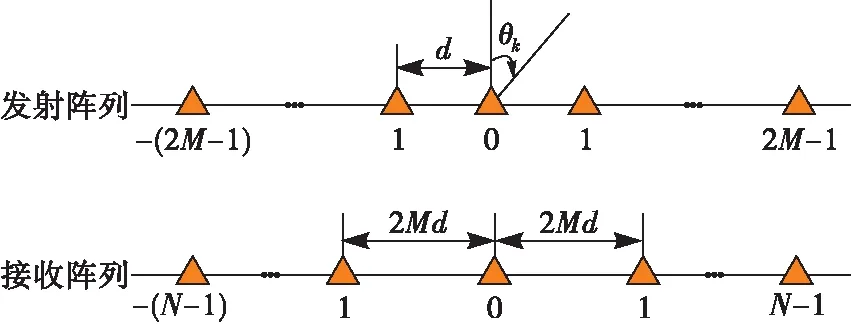
图1 单基地对称嵌套MIMO雷达结构图

假设空间中存在K个远场点目标，第k(k=1,2,…,K)个目标的波达方向和反射系数分别为θk和βk，则单基地对称嵌套MIMO雷达回波信号模型可表示为：

(1)

式中：b(t)=[b-(2M-1)(t),…,b(-1)(t),b0(t),b1(t),…,b(2M-1)(t)]T为发射信号；w(t)=[ω-(N-1)(t),…,ω(-1)(t),ω0(t),ω1(t),…,ω(N-1)(t)]T为接收阵元处的加性高斯白噪声；αt(θk)和αr(θk)分别为第k个目标的发射导向矢量和接收导向矢量，具体可表示为：

αt(θk)=[ej2πdQsin θk/λ,…,1,…e-j2πdQsin θk/λ]T

αr(θk)=[ej2π(2Md)Psin θk/λ,…,1,…e-j2π(2Md)Psin θk/λ]T

(2)

式中：Q=2M-1；P=N-1。

利用MIMO雷达发射波形为相互正交脉冲信号，即Rb=E[b(t)b(t)H]=I4M-1的特点,将回波信号进行广义匹配滤波可得：

[αt(θ1)⊗αr(θ1),…,αt(θK)⊗αr(θK)]s(t)+

n(t)=(At⊙Ar)s(t)+n(t)

(3)

式中：At=[at(θ1),at(θ2),…,at(θK)]；Ar=[ar(θ1),ar(θ2),…,ar(θK)];s(t)=[β1,β2,…,βK]T；n(t)为加性高斯白噪声矢量；⊗和⊙分别表示Kronecker积和Khatri-Rao积。

根据式(3)可得回波信号的协方差矩阵为：

R=E[x(t)x(t)H]=

(4)

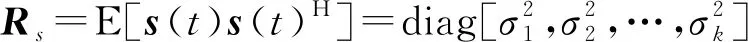
向量化协方差矩阵R可得：

r=vec(R)=

(5)

式中：vec(·)表示向量化运算；

(6)

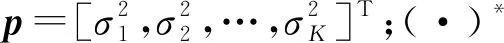
2 对称嵌套MIMO雷达虚拟阵元扩展

如图1所示，可得发射阵列阵元位置集合St为：

(7)

接收阵列阵元位置集合Sr为：

(8)

由式(3)可知，矩阵A=At⊙Ar的虚拟阵元位置由物理阵元位置的“和联合阵列”组成。具体分为以下4种情况：

(9)

由式(6)可知，矩阵A*⊙A的虚拟阵元位置由物理阵元位置的“和差联合阵列”组成。即：

(10)

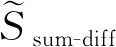
通过以上分析可知，“和联合阵列”和“和差联合阵列”可以实现对称嵌套MIMO雷达虚拟孔径扩展，进一步提升自由度。

3 DOA估计

3.1 非相干目标DOA估计

根据式(9)，可从式(3)中选取与扩展后的虚拟阵元位置对应的数据，重新排列后建立新的观测矢量：

x0(t)=A0s(t)+n0(t)

(11)

式中：A0=[a0(θ1),…,a0(θK)]，n0(t)为对应位置的噪声矢量，且a0(θk)=[ej2πdZsinθk/λ,…,1,…,e-j2πdZsinθk/λ]T，其中，Z=2MN-1。

由式(11)可得协方差矩阵为：

(12)

因此，通过“和联合阵列”估计非相干目标，可对式(12)进行特征值分解，然后采用MUSIC算法进行DOA估计。

非相干目标DOA估计也可以从“和差联合阵列”角度求解，将A*⊙A中虚拟阵元进行冗余平均，并按照虚拟阵元位置从小到大重新排序，可构造(8MN-3)×K维的方向矩阵A1：

[a(θ1),a(θ2),…,a(θK)]

(13)

式中：Lε(1≤ε≤8MN-3)为式(10)中第ε个虚拟阵元位置的冗余度，即“和差联合”阵列中虚拟阵元出现的次数；Bε(θk)为A*⊙A中能形成同一虚拟阵元位置的导向矢量的叠加；a(θi)=[e-jβiz1,e-jβiz2,…,e-jβiz8MN-3]，其中βi=2πsinθi/λ，zε(1≤ε≤8MN-3)为虚拟阵元位置。

此时，相应的回波信号矢量为：

(14)

为充分利用扩展的虚拟阵元，利用r1建立Toeplitz矩阵如下：

(15)

式中：

(16)

式中：zε和zμ均为虚拟阵元位置，ε,μ=1,2,…,8MN-3(ε+μ≤8MN-3),则式(15)可以写成矩阵的形式：

(17)

式中：pi为p中的第i个元素；nε为第ε个虚拟阵元中的高斯白噪声。

(18)

(19)

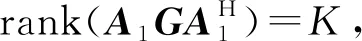
(20)

总结本文算法的具体步骤，见表1。

表1 基于虚拟阵元冗余平均的对称嵌套MIMO雷达DOA估计算法算法步骤

3.2 全相干目标DOA估计

全相干目标DOA估计，采用“和联合”阵列求解。根据式(12)，可利用空间平滑技术结合MUSIC算法求解目标角度，但会损失扩展的虚拟阵元孔径。因此，本文采用1-SVD算法[15]进行DOA估计。此时，全部的虚拟阵元都可以利用，角度估计性能更佳，具体步骤见表2。

表2 1-SVD算法步骤

步骤1:根据式(11)获得观测矢量x0(t);步骤2:对观测矢量x0(t)进行奇异值分解;步骤3:对观测矢量x0(t)和稀疏信号进行降维(观测矢量维度由阵元数×快拍数降为阵元数×信源数,稀疏信号维度由网格数×快拍数降为网格数×信源数);步骤4:求稀疏信号的ℓ1范数;步骤5:利用CVX工具箱进行凸优化处理,求得目标角度。

通过“和差联合阵列”进行全相干目标DOA估计时，单快拍测量矢量r的虚拟阵列方向矩阵中不同导向矢量之间由Khatri-Rao积关系变为Kronecker积，信源协方差矩阵由对角阵变为块对角阵，其非主对角元素为非零值。因此，需要估计更多的元素，导致其难以应用于全相干目标的测向。

4 克拉美罗界(Cramér-Rao Bound, CRB)

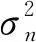
定义DOA角度矢量为：

η=[θ1,θ2,…,θK]T

(21)

由文献[15]可知Fisher信息矩阵的第i行第j列元素为：

(22)

式中：tr[·]表示矩阵的迹；ηi和ηj分别表示矢量的第i个和第j个元素。

假设

(23)

则式(22)可表示为：

(24)

其中，

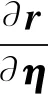
(25)

Ad=D*⊙A+A*⊙D

(26)

(27)

由于R为正定矩阵，(R⊗R)-1和(R⊗R)-1/2均为正定矩阵。则式(24)可写为：

FIM=LFHF

F=(R⊗R)-1/2ΑdP0,P0=blkdiag[Rs,Rs]

(28)

由此可得DOA估计方向的CRB为：

(29)

5 仿真实验和结果分析

5.1 场景设定

假设单基地对称嵌套MIMO雷达的发射和接收阵列的阵元数分别为Mt=7，Nr=5，即M=2，N=3，相应地设定传统MIMO雷达的发射阵列和接收阵列阵元个数分别为6，二阶嵌套MIMO雷达发射阵列和接收阵列均采用6阵元的嵌套阵，DOA估计的均方误差(RMSE)的计算表达式为(共200次蒙特卡洛实验):

(30)

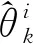
5.2 自由度和互耦率

5.2.1 自由度

表3给出了“和联合阵列”和“和差联合阵列”结构下传统MIMO、二阶嵌套MIMO和对称嵌套MIMO 雷达的物理阵元数、连续虚拟阵元数和总虚拟阵元数。从表3中可以看出，3种MIMO雷达物理阵元数相同，但对称嵌套MIMO雷达在“和联合阵列”条件下能够获得更多的连续虚拟阵元和总阵元数。对于向量化的样本协方差矩阵，二阶嵌套MIMO和对称嵌套MIMO雷达得到相同的连续虚拟阵元和总虚拟阵元数。

表3 不同阵列结构虚拟阵元数

5.2.2 互耦率

根据文献[17]，可求出不同阵列结构收发阵元互耦率，如表4所示。其中，Ωt和Ωr分别表示发射阵列和接收阵列的互耦率，互耦矩阵中的元素满足c0=1，c1=0.5ejπ/4，c2=0.5ej0.5π/2，c3=0.5ej0.5π/3，c4=0.5ej0.5π/4，B=4。由表4可知，对称嵌套MIMO雷达因接收阵元采用阵元间距更大的稀疏均匀线阵，相比于传统MIMO和二阶嵌套MIMO雷达，其互耦率大幅降低。

表4 不同阵列结构的互耦率

5.3 空间谱

本节比较了不同类型MIMO雷达可检测目标个数。假设信噪比为10 dB，快拍数为500，搜索范围为[-90°,90°]，搜索步长为0.01°，红色点画线表示真实角度方向。

5.3.1 非相干目标DOA估计

图2给出了“和联合阵列”结构下不同阵列结构的空间谱图。对二阶嵌套MIMO雷达形成的虚拟阵元选取连续部分，结合式(12)，采用MUSIC算法进行DOA估计。假设空间中存在20个非相干目标，由图2可知，传统MIMO雷达能够估计[-40°∶10°∶40°]的9个非相干目标，二阶嵌套MIMO雷达能够估计[-60°∶10°∶60°]的13个非相干目标，而对称嵌套MIMO雷达能够估计[-70°∶7°∶63°]的20个非相干目标，且目标角度间隔最小。因此，通过利用对称“和联合阵列”提升虚拟阵元个数，对称嵌套MIMO雷达能够估计更多的非相关目标。

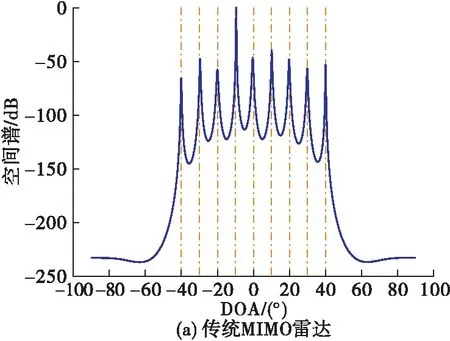
图2 “和联合阵列”结构下非相干目标空间谱

图3给出了“和差联合阵列”结构下对称嵌套MIMO雷达和二阶嵌套MIMO雷达空间谱图。假设DOA角度为[-70°∶7°∶63°]，采用3.1节所提算法进行角度估计。由图3可知，对称嵌套MIMO雷达和二阶嵌套MIMO雷达均能够估计20个非相干目标。

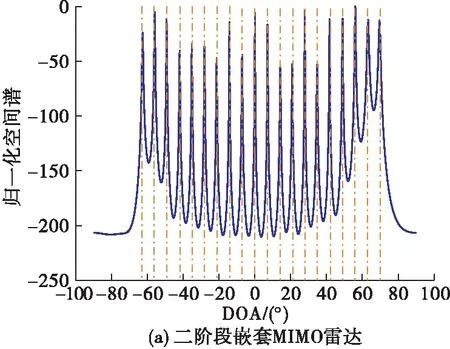
图3 “和差联合阵列”结构下非相干目标空间谱

5.3.2 全相干目标DOA估计

图4给出了“和联合阵列”结构下不同阵列结构的空间谱图。假设DOA角度为[-50°∶10°∶50°]，目标之间相干系数设为1。

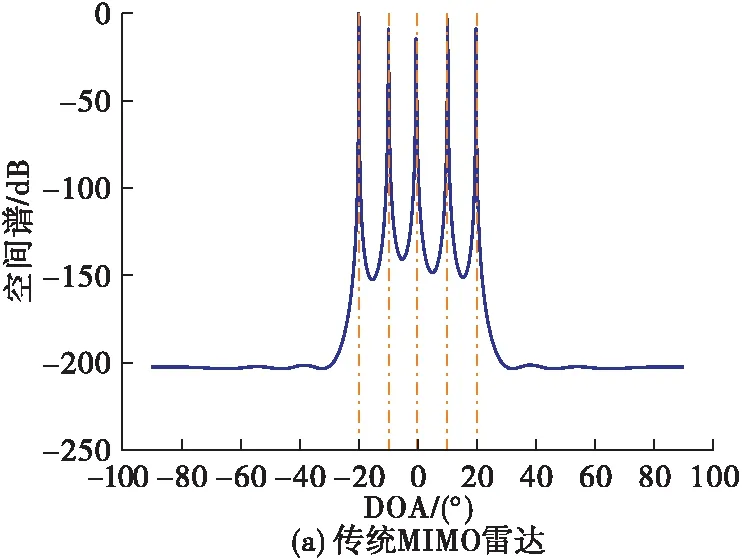
图4 “和联合阵列”结构下全相干目标空间谱

由图4可知，传统MIMO雷达能估计[-20°∶10°∶20°]，即5个全相干目标；二阶嵌套MIMO雷达能估计[-30°∶10°∶40°]，即8个全相干目标；而对称嵌套MIMO雷达能够估计全部11个全相干目标。因此，通过利用对称“和联合阵列”提升虚拟阵元个数，对称嵌套MIMO雷达能够估计更多的相干目标。

5.4 均方误差

假设目标的角度为θ1=10°，θ2=20°，θ3=30°，搜索步长为0.01°。

5.4.1 非相干目标DOA估计均方误差

图5给出了“和联合阵列”结构下不同阵列结构的均方误差对比图。图5(a)为DOA估计误差随信噪比的变化关系图，其中快拍数为500。图5(b)为DOA估计误差随快拍数的变化关系图，其中SNR=10 dB。结合图5和表3可以看出，对称嵌套MIMO雷达在“和联合阵列”结构下能够得到更多的连续虚拟阵元数和总阵元数。因此，估计性能更好。

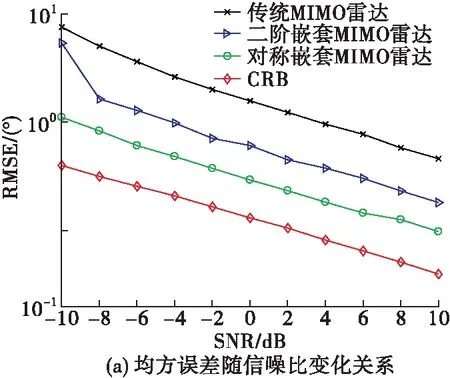
图5 “和联合阵列”结构下非相干目标估计性能对比

图6给出了“和差联合阵列”结构下不同阵列结构的均方误差对比图。

图6 “和差联合阵列”结构下非相干目标估计性能对比

图6(a)为DOA估计误差随信噪比的变化关系图，其中快拍数为500。图6(b)为DOA估计误差随快拍数的变化关系图，其中SNR=10 dB。结合图6和表3可以看出，对称嵌套MIMO雷达和二阶嵌套MIMO雷达在“和差联合阵列”结构下连续的虚拟阵元和总阵元数均相同。因此，两者估计性能接近。

5.4.2 全相干目标DOA估计均方误差

图7给出了“和联合阵列”结构下不同阵列结构的均方误差对比图。图7(a)为DOA估计误差随信噪比的变化关系图，其中快拍数为500。图7(b)为DOA估计误差随快拍数的变化关系图，其中SNR=10 dB。结合图7和表3可以看出，对称嵌套MIMO雷达可利用“和联合阵列”得到更多连续的虚拟阵元和总阵元数，因此，其估计性能更佳。

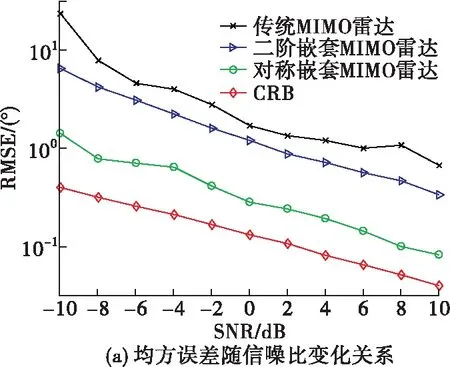
图7 “和联合阵列”结构下全相干目标估计性能对比

5.5 角度分辨率

以“和联合阵列”结构下全相干目标的角度分辨率为例。假设2个全相干邻近目标3°和6°，信噪比SNR=10 dB,快拍数为500，搜索范围为[0°,10°]，步长为0.1°，黑色点画线表示真实角度方向。由图8可知，传统MIMO雷达无法分辨上述两个目标，而二阶嵌套MIMO雷达和对称嵌套MIMO雷达可以分辨，且对称嵌套MIMO雷达测向精度更高，谱峰更尖锐。

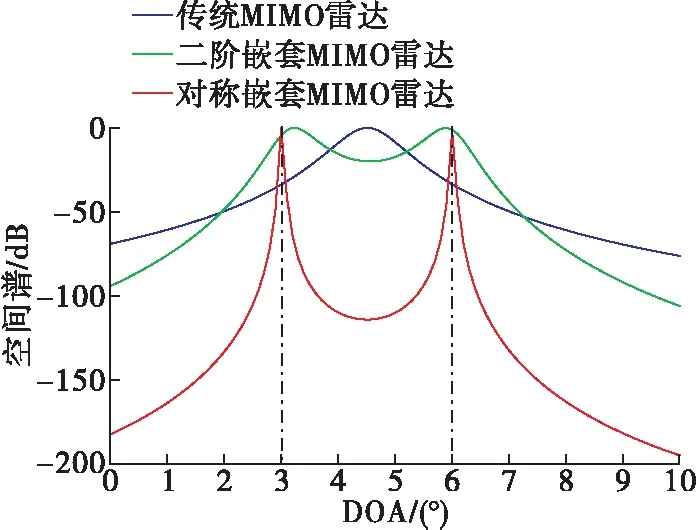
图8 “和联合阵列”结构下邻近全相干目标空间谱

6 结语

本文将阵列的“差联合”阵列结构变成了对称“和联合”阵列结构，提升了自由度性能、抑制了接收阵元互耦，并将其应用于全相干和非相干目标DOA估计，提升了目标估计个数和角度估计性能；针对传统算法通常采取删除嵌套阵列的重复虚拟阵元进行DOA估计时存在数据丢失问题，算法向量化协方差矩阵，对“和差联合阵列”形成的虚拟阵元进行冗余平均处理后重构Toeplitz矩阵，充分利用了所有的扩展虚拟阵元，结合MUSIC算法实现了欠定条件下目标DOA估计。仿真实验表明本文所提阵列结构和算法提高了多目标角度估计性能和精度。