两级串联超前校正网络飞行器控制系统设计

李瑀馨

（武汉理工大学 自动化学院，湖北 武汉430070）

1 任务要求

已知一飞行器控制系统开环传递函数为：

控制系统性能指标：调节时间小于0.01s，单位斜坡输入的稳态误差小于0.0005，相角裕度大于80°。

本文首先分析校正前系统的稳定性、动态特性等，对系统状况有了初步的了解。根据实际情况选择合适的校正装置，使得校正后的装置满足设计要求，并对校正前后系统进行对比分析。

2 校正前系统性能分析

2.1 校正前系统的稳定性分析

一般情况下，确定线性系统稳定性的方法分为基于经典控制理论和基于现代控制理论的方法。

经典控制论中，以传递函数或频率特性的形式来描述控制系统，稳定判据有：劳斯稳定判据、根轨迹法和奈奎斯特稳定判据等。

本文基于经典控制理论的稳定性判据，以确定特征根所在区域为目的，由此判断系统的稳定性[1-2]。

2.1.1 劳斯稳定判据

劳斯判据法可根据系统特征方程式系数判断系统的稳定性。这种方法比较简单，但只能判断系统是否稳定，不能判断系统的稳定程度。它可以用于飞行器控制系统设计阶段，判断所设计的飞行器控制系统稳定性。

针对给定的飞行器控制系统的开环传递函数，由系统的开环传函可知此系统为一个二阶系统。因此，可求得飞行器控制系统的系统特征方程为：

列出劳斯表如表1所示。

表1 飞行器控制系统的劳斯表

通过表1可以看到，要使系统稳定，即第一列为正，则K必须大于0。

2.1.2 系统根轨迹判定

根轨迹是分析和设计线性定常控制系统的图解方法，使用十分简便，特别在进行多回路系统的分析时，应用根轨迹法比用其他方法更为方便，因此在工程实践中获得了广泛应用[3]。本文利用Matlab进行编程[4]，绘制出飞行器控制系统开环传递函数随K变化的根轨迹图。

由根轨迹图可知当K＞0，根轨迹不会越过虚轴进入右半s平面，因此这个系统对所有的K值都是稳定的。当0＜K＜7.25时，闭环极点位于实轴上，系统为过阻尼系统；当K=7.25时，闭环极点重合，系统为临界阻尼系统，响应速度较0＜K＜7.25情况快；当K＞7.25时，闭环极点为复数极点，系统为欠阻尼系统，超调量随K的增大而增大，但调节时间的变化不显著。

2.1 .3 奈奎斯特稳定判据

奈奎斯特稳定判据对系统稳定性进行判别时根据系统的开环频率特性。P为开环传递函数在右半s平面上的极点数。N为轨迹沿逆时针方向包围实轴上点（-1，j0）的次数。闭环控制系统正实部极点数：Z=P-R。奈奎斯特稳定判据指出Z=0时，闭环控制系统稳定；Z≠0时，闭环控制系统不稳定。

利用Matlab绘制未校正系统的奈奎斯特曲线，并进行判断。可知R=0，P=0，由Z=P-R可得，Z=0，说明K＞0时系统一直处于稳定状态，与上述劳斯稳定判据、根轨迹判定结果一致。

2.2 系统伯德图与系统幅值裕度、相角裕量

利用伯德图可以看出在不同频率下系统增益的大小及相位，也可以看出增益大小及相位随频率变化的趋势，还可以对系统的稳定性进行判断。

本文利用Matlab编程仿真[5]绘制了系统的伯德图。通过观察绘制的伯德图可以看出未校正前控制系统的相角裕度随K值的增大而增大，且未校正前控制系统的幅值裕度和相角裕度均为正值，进而可得未校正前控制系统为稳定系统，与上述论证结果一致。

2.3 单位阶跃输入状态下的系统响应

为了进一步观察系统的动态性能，本文利用Matlab编程仿真，观察未校正系统在单位阶跃输入和单位斜坡输入下的响应情况。单位阶跃输入分为过阻尼、临界阻尼、欠阻尼状态，以此研究系统的动态性能。求得的3种状态下的动态性能指标如表2所示。

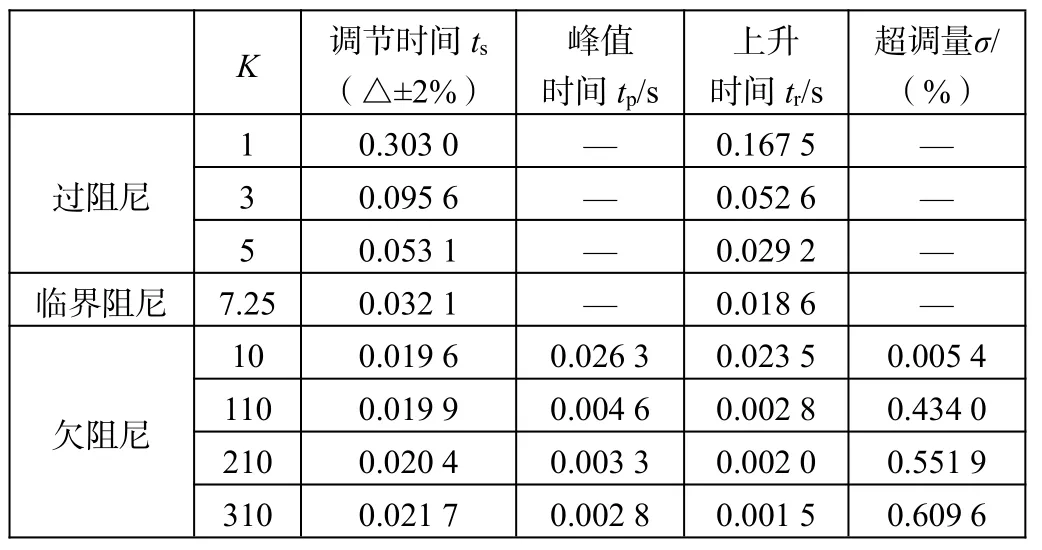
表2 3种状态下动态性能指标

由表2可以观察到过阻尼状态系统调节时间和上升时间随K的增大而缩短，临界阻尼系统响应速度较过阻尼情况快；欠阻尼峰值时间和上升时间随K的增大而缩短，且超调量将随K的增大而增大，但调节时间的变化不太显著，并且可以清楚地看出系统处于稳定状态，与前述分析结果一致。

3 飞行器控制系统的校正

3.1 系统K值的确定

系统要求单位斜坡输入的稳态误差小于等于0.0005，根据单位斜坡输入的稳态误差定义可做出如下计算。

由前面分析可知此系统处于欠阻尼状态，峰值时间和上升时间随K的增大而缩短，且超调量将随K的增大而增大，但调节时间的变化不显著。因此，方便计算综合可取K=161。

可计算得到系统的调节时间ts=0.199s（△=±2%），wc=813.72rad/s，相角裕度γ=23.94°。

3.2 两级串联超前校正网络设计

要将待校正系统的相角裕度提高到大于80°。由于串联校正a不能过大，想要达到目标相角裕度，至少选用两级串联超前网络。

根据上述设计步骤，本文针对给出的控制系统和相应的性能指标要求等，设计对应的串联超前校正装置，具体参数计算与设计过程如下所示[6-7]。

3.2.1 设计第一级串联超前校正网络[7]

根据稳态性能要求，确定开环增益K=724500。

求出未校正系统的截止频率wc0=813.72rad/s，相角裕度γ0=23.94°。

利用超前校正网络将相位裕度校正到γ1=60°，计算需要产生的最大超前角φm=γ1-γ0+（5°～10°）=60-23.94+（5°～10°）≈45°。

令校正后wc=wm。

确定校正装置的传递函数：

3.2.2 设计第二级串联超前校正网络

求出第一级校正后系统的截止频率wc1=1217.9rad/s，相位裕度γ1=61.09°。

利用超前校正网络将相位裕度校正到γ2＞80°，计算需要产生的最大超前角φm=γ2-γ1+（5°～10°）≈25°。

根据所需要最大超前角求出a=2.47。

校验已校正系统的各项性能指标，求得截止频率wc1=1217rad/s，相位裕度γ1=81.21°，调节时间ts=0.0049s。单位斜坡输入的稳态误差为0.00049855。综上所述，校正后系统满足题目设计要求。

4 校正后系统性能分析

4.1 校正后系统根轨迹

绘制校正后系统根轨迹如图1所示。由图1可知根轨迹不会越过虚轴进入右半s平面，因此这个系统对所有的K值都是稳定的。

图1 校正后系统根轨迹

4.2 校正后奈奎斯特稳定判据判稳

绘制校正后系统奈奎斯特曲线如图2所示。通过奈奎斯特曲线可以得出R=0，P=0，所以根据Z=P-R可得Z=0，说明没有闭环极点位于右半s平面，所以系统处于稳定状态，与上述根轨迹判定结果一致。

图2 校正后系统奈奎斯特曲线

4.3 系统伯德图与系统幅值裕度、相角裕度

绘制校正前后系统的伯德图，求出的幅值裕量和相角裕量如表3所示。

表3 幅值裕度和相角裕度

可以看出校正前后控制系统的幅值裕度和相角裕度均为正值，进而可得校正前后控制系统为稳定系统，且校正后系统满足设计要求。

4.4 校正后系统单位阶跃输入状态下的系统响应

为了进一步观察系统的动态性能，本文利用Matlab编程仿真，观察校正前后系统在单位阶跃输入下的响应情况，具体的仿真结果如图3所示，可见系统可较好地跟踪上阶跃信号，且比原系统跟踪信号的能力显著提高。计算出系统动态性能指标，如表4所示。

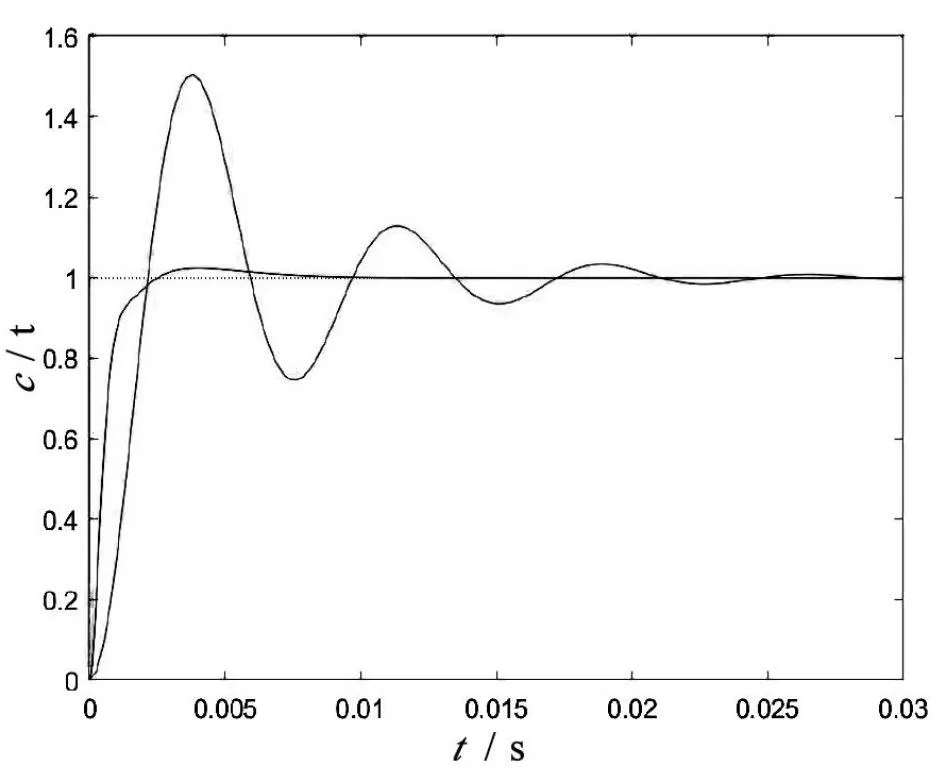
图3 单位阶跃输入下系统响应

表4 系统动态性能指标

由表4可知，校正后调节时间显著缩短，峰值时间和上升时间基本不变，超调量显著减小，可见校正后系统的性能显著提升。

本文设计的两级串联超前校正装置很好地满足了设计要求，而且校正后系统快速性、稳定性、跟踪信号能力方面都有显著提升。