基于铺覆模拟的复合材料螺旋桨叶片实体有限元建模分析
2020-03-26李雪芹郭双喜
李雪芹 陈 科 郭双喜
(1 航空工业复合材料技术中心,中航复合材料有限责任公司,先进复合材料重点实验室,北京 101300)
(2 海军研究院,北京 100161)
文 摘 为了评估复合材料螺旋桨叶片在铺覆时纤维取向改变对性能的影响,基于Fibersim 软件的铺覆模拟结果建立了复合材料螺旋桨叶片的实体有限元模型,并与不考虑纤维取向改变时的有限元计算结果进行对比。结果表明:不考虑纤维取向改变时叶片固有频率及均布压力下最大位移误差小于5%,但热载荷下考虑真实纤维方向时的最大变形量约为不考虑真实纤维方向时的2倍,叶片局部区域0°、45°、-45°方向铺层的纤维角度偏差超过了25°。在进行复合材料螺旋桨叶片有限元分析时应基于铺覆后的真实纤维方向。
0 引言
传统的金属螺旋桨存在噪音大、不耐海水腐蚀、疲劳寿命不长等问题,将纤维增强复合材料应用于船用螺旋桨叶片上将有助于改善这些问题,因此具有巨大的潜力[1-2]。瑞典在21 世纪初已经在其皇家海军Vikten 扫雷艇上安装了三叶碳纤维复合材料螺旋桨,2014年日本载重499 t 的运输船“太鼓丸”号的主推进系统安装了五叶碳纤维复合材料螺旋桨[3]。近年来,复合材料螺旋桨叶片的铺层角度优化[4-5]、流-固耦合[6-7]、振动阻尼[8-9]等方面是研究的重点,但对于复合材料叶片的成型制造过程及其对叶片性能的影响涉及较少。螺旋桨叶片这类空间形状复杂的复合材料构件可直接采用三维机织或编织获得三维复合材料构件预成型体,再采用RTM 工艺方法成型;虽然国外该技术已在航空发动机叶片上应用[10-11],但是这种工艺方法难度大、成本高、周期长。采用二维平面单向或多向织物通过铺覆来制造三维复杂结构仍是复合材料构件主要采用的工艺方法[12-14]。
在对二维平面织物制得的复合材料螺旋桨叶片进行设计分析时,需要重点关注纤维在铺覆过程中的变形问题。在铺覆过程中,纤维会通过变形进行重新分布以适应复杂的三维铺覆面,并且纤维的方向也会发生变化[15-17]。纤维方向的改变对复合材料结构的性能有着重要影响,在设计时必须考虑真实的纤维方向[18-20]。对于复合材料螺旋桨叶片来说,因其叶形呈空间自由曲面状,造成复合材料在铺覆时纤维方向变化较大,基于铺覆模拟的有限元建模分析研究有着重要意义。采用商用铺覆模拟软件Fibersim可以对复合材料的铺覆过程进行模拟,再将模拟后纤维取向导入到CAE软件中进行进一步的结构分析。Fibersim软件导出的铺覆模拟结果既可以用于壳单元也可以用于实体单元。在文献[21]中,已对船用复合材料螺旋桨叶片的有限元建模方法进行了讨论,采用壳单元前处理所需时间一般较长,且计算叶片热载荷下的响应时是不适用的。因此,本文将采用实体单元进行建模及分析。先采用Fibersim软件对叶片曲面上的纤维铺覆过程进行模拟,然后基于Fibersim软件铺覆模拟后叶片各处的真实纤维方向进行船用复合材料螺旋桨的实体有限元建模,并分析不同工况下叶片的响应,比较考虑和不考虑真实纤维方向两种情况下叶片的前三阶模态、表面均布压力下的变形和热载荷下的变形结果,讨论基于铺覆模拟的有限元建模分析技术对于复合材料螺旋桨叶片结构的有效性和适用性。
1 实验材料及结构
1.1 材料
T300碳纤维增强环氧树脂复合材料性能见表1[21]。

表1 碳纤维增强复合材料性能Tab.1 Properties of carbon fiber reinforced composite
1.2 螺旋桨结构
研究对象为图1 所示旋转直径为3.16 m 的五叶船用螺旋桨,具体尺寸参见文献[21]。

图1 船用复合材料螺旋桨Fig.1 Composite marine propeller
1.3 有限元模型
有限元建模前的叶片几何模型处理方法[21]如图2 所示,划分为叶面和叶背两部分,再将叶片两部分各自的中面提取出来,用于Fibersim 软件铺覆模拟。被中面划分开的两部分叶片沿其厚度方向只划分1个单元,将Fibersim 软件铺覆模拟结果映射到每个单元中心点上。
采用ANSYS软件进行船用复合材料螺旋桨叶片建模及计算,最终的有限元模型见图3,包含17 918个六面体单元和97 749 个节点,单元的z方向与叶片中面的法线方向基本一致。
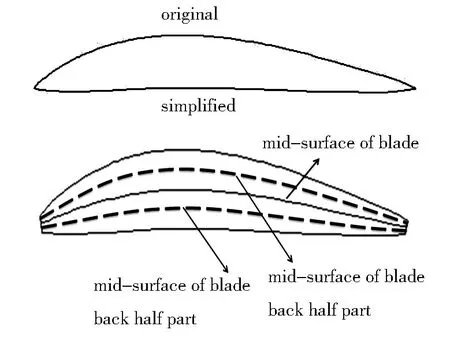
图2 叶片几何模型处理示意图Fig.2 Geometric model processing of propeller blade
1.4 铺层与等效的材料参数
叶片的铺层方式是从叶背表面到叶片中面以及从叶面表面到叶片中面顺序铺设,叶背和叶面的铺层数量相同。
采用[0/45/0/-45]sn对称铺层考察纤维方向的变化以及对计算结果的影响,叶片各处铺层均一致。铺层角为纤维方向和单元x方向之间的夹角。不考虑真实纤维方向时,采用等效的各向异性材料参数进行计算,对应[0/45/0/-45]sn铺层的等效性能参数如表2所示。

表2 材料的等效性能Tab.2 Equivalent properties of materials
2 结果与讨论
2.1 铺覆模拟
采用Fibersim 软件依据铺覆面上各铺层的边界及角度定义进行复合材料铺覆模拟。以叶背中面为铺覆面的铺层边界如图4所示,由于桨叶厚度在不断变化各铺层的铺覆面积也在逐渐缩小。叶面中面为铺覆面时铺层边界与图4类似并一一对应。

图4 叶背中面上的铺层边界Fig.4 Ply boundaries on mid-surface of blade back
叶背部分中面处0°铺层的模拟结果如图5所示,图中不仅显示了叶片从叶根到叶尖各处真实的纤维方向,还显示了纤维发生变形的区域和变形量。在叶身中部和靠近导边的叶片局部铺覆的纤维均有较大的变形。
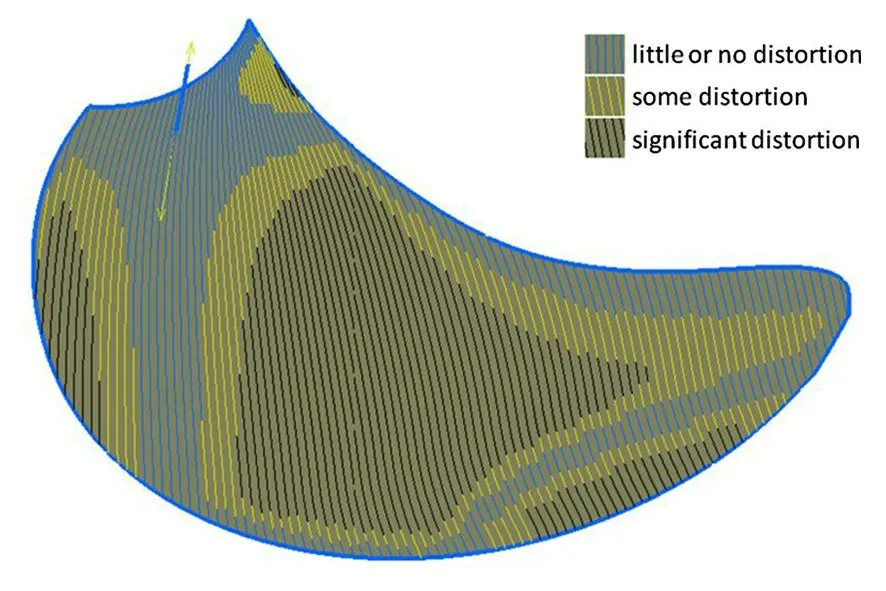
图5 叶背中面0°铺层铺覆模拟变形结果Fig.5 Distortion result of 0°ply draping simulation on mid-surface of blade back
纤维铺覆变形会导致铺层的角度产生偏差。图6 显示了叶背中面各角度铺层纤维偏差的铺覆模拟结果。
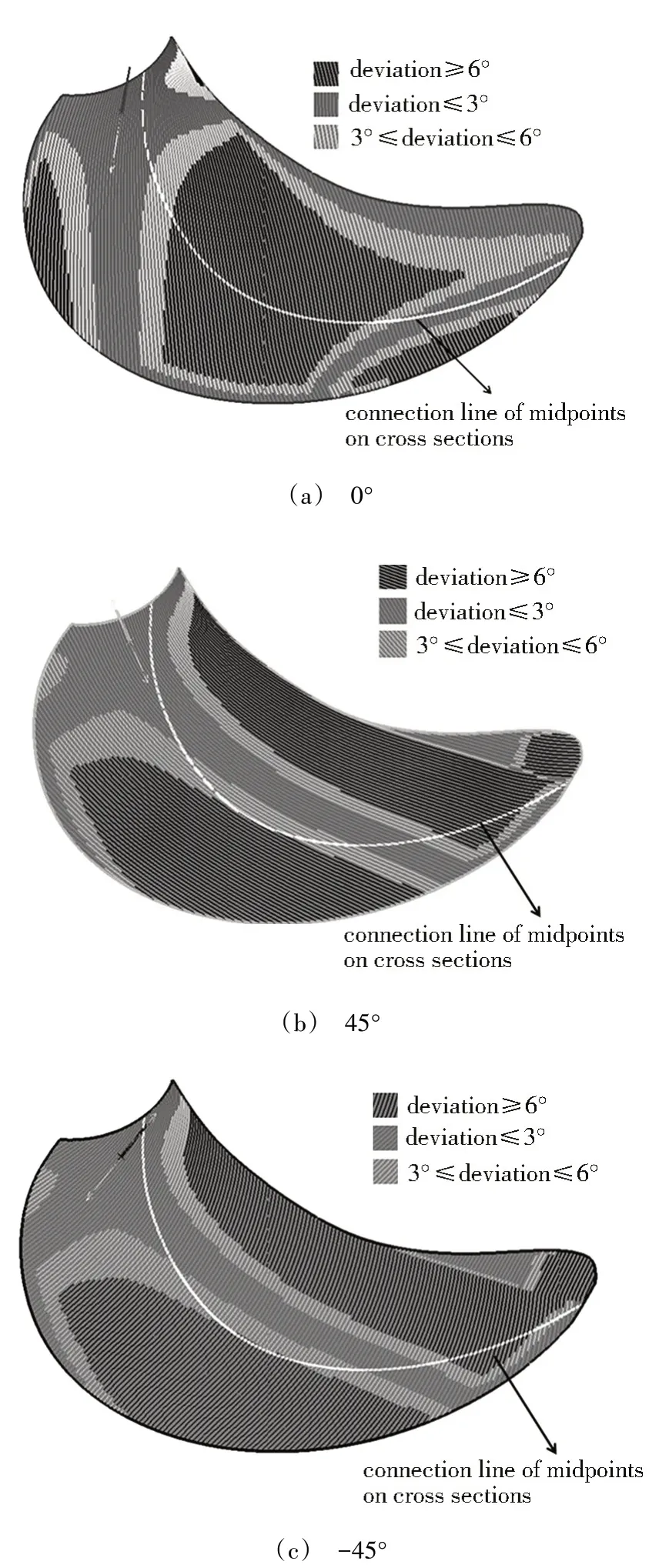
图6 叶背中面铺覆模拟角度偏差结果Fig.6 Deviation results of draping simulation on midsurface of blade back
图6(a)中0°铺层在叶身中部和导边有较大的变形,真实纤维角度与设计角度相比偏差大于6°;除此以外,还可以看出纤维取向与桨叶截面中点的连线之间的夹角从叶根到叶尖不断变大,叶尖处接近90°。图6(b)中45°铺层在随边和导边附近有纤维角度偏差大于6°的较大变形;纤维取向与桨叶界面中点的连线之间的夹角从叶根开始由45°逐渐减小,到叶身中部接近0°,到叶尖处夹角又增加到-45°左右。图6(c)中-45°铺层纤维角度偏差较大的位置与45°铺层相似;纤维取向与桨叶界面中点的连线之间的夹角从叶根开始由-45°逐渐增加至接近90°,到叶尖处夹角仍较大。叶面中面上的模拟结果与图6相似。
2.2 模态分析
不考虑真实纤维方向时,均匀分布铺层的螺旋桨叶片模态分析结果如图7 所示。叶片前三阶频率分别为57.0、127.2 和165.4 Hz。采用Fibersim 软件进行铺覆模拟,得到真实纤维方向后,计算得到的叶片模态分析结果如图8 所示。均匀分布铺层的螺旋桨叶片模态计算固有频率结果见表3。对于均匀分布铺层的螺旋桨叶片来说,纤维方向的改变对频率结果影响小于5%,振型也仅有微小的区别。

图7 不考虑纤维方向改变的叶片模态分析结果 2×Fig.7 Modal analysis results of propeller blade ignoring fiber direction deviation
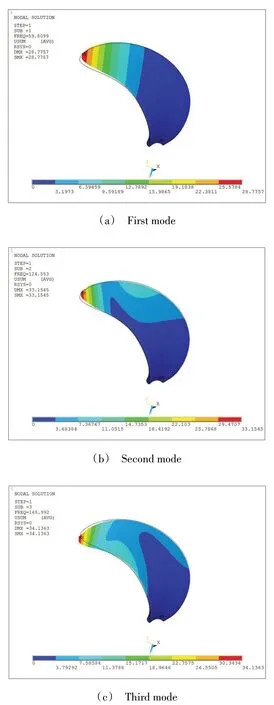
图8 考虑纤维方向改变的均匀分布铺层叶片模态分析结果 2×Fig.8 Modal analysis results of propeller blade considering fiber direction deviation
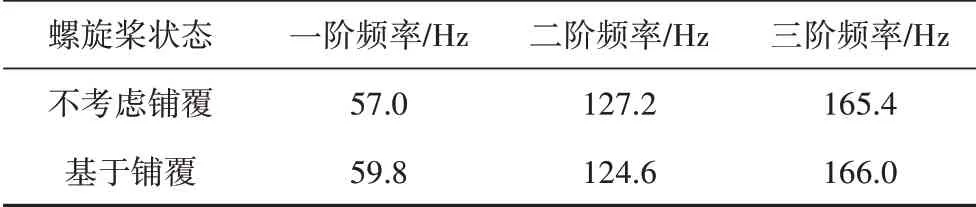
表3 固有频率计算结果Tab.3 The results of natural frequency
2.3 均布压力载荷及热载荷响应分析
固支约束桨叶与桨毂的连接面,在叶面表面施加0.1 MPa的均布压力,螺旋桨叶片的最大变形量如表4 所示。表4 中也显示了同样的约束条件下,固化后从180℃冷却至20℃过程中螺旋桨叶片产生的最大位移。图9 为均布压力载荷下复合材料螺旋桨叶片的位移分布,图10 为热载荷下复合材料螺旋桨叶片的位移分布。
由表4 和图9 可以看出,均布压力载荷下复合材料螺旋桨叶片的变形两种模型计算结果差异小于3%,这说明纤维方向的变化并未对叶片的整体弯曲刚度造成太大的影响。由表4 和图10 可以看出,热载荷下复合材料螺旋桨叶片两种模型的计算结果差异很大,考虑真实纤维方向时的变形量约为不考虑真实纤维方向时变形量的2倍。
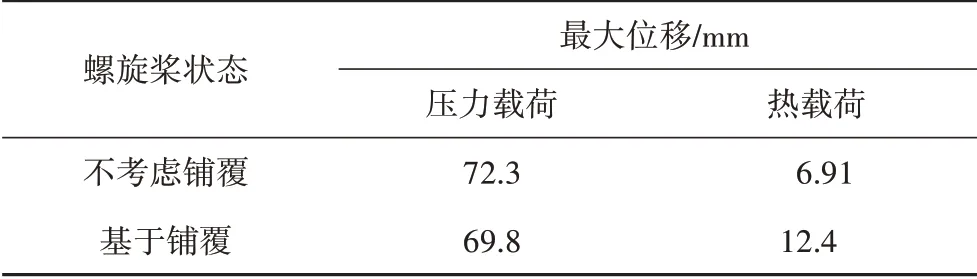
表4 均布压力载荷及热载荷下的分析结果Tab.4 Results of uniformly distributed pressure loads and thermal loads
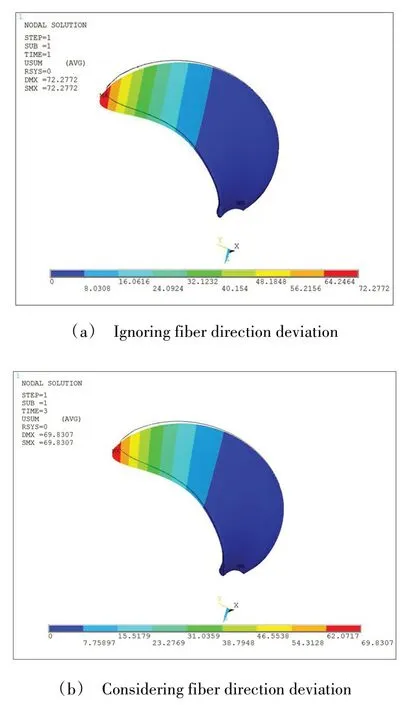
图9 均布压力载荷下的分析结果 2×Fig.9 Results of propeller blade under uniformly distributed pressure loads

图10 热载荷下叶片的分析结果 10×Fig.10 Results of propeller blade under uniformly distributed thermal loads
2.4 纤维取向变化及其影响
由图6可知,纤维铺覆变形会导致铺层的角度产生偏差,局部区域纤维角度偏差大于6°。为了对纤维取向变化进行定量分析,在叶面中面上取铺覆原点和典型位置上的4个点,获取这些点所在位置局部坐标系下的纤维角度,纤维实际角度与设定角度之间的偏差代表纤维取向变化的具体数值。铺覆原点及4 个标记点的位置如图11 所示。0°、45°及-45°铺层在铺覆原点及4 个标记点处的对应角度如表5 所示。可以看出,从叶根往叶尖方向0°方向的铺层在局部坐标系下的角度与设定角度之间的偏差先逐渐增加然后减小,最大角度偏差超过35°。45°方向的铺层在起始时接近设计角度,但越靠近叶尖角度偏差越大,最大角度偏差超过25°。-45°方向的铺层在起始时以及点1、点3处接近设计角度,在其他2点处角度都发生较大变化,最大角度偏差超过30°。
从模态分析及均布压力载荷下复合材料螺旋桨叶片的变形可以看出,纤维取向的改变对这两种工况的结果影响很小,这可能是不同部位纤维取向改变综合作用的结果。而热载荷下不考虑纤维真实方向时复合材料螺旋桨叶片的变形的计算误差较大,差异主要是靠近叶尖的区域变形急剧增加造成的。靠近叶尖的区域厚度较薄,线胀系数的不匹配更容易造成叶尖局部变形;纤维取向变化后,叶尖局部变形方式也发生较大变化,因此叶片在热载荷下的最大变形受到纤维取向变化的影响较大。总体上看,由于复合材料螺旋桨叶片铺覆面是复杂的空间曲面,因此纤维方向的变化规律比较复杂,纤维取向改变对复合材料螺旋桨叶片响应的影响规律也比较复杂,基于铺覆模拟进行复合材料螺旋桨叶片实体有限元建模分析是十分必要的。
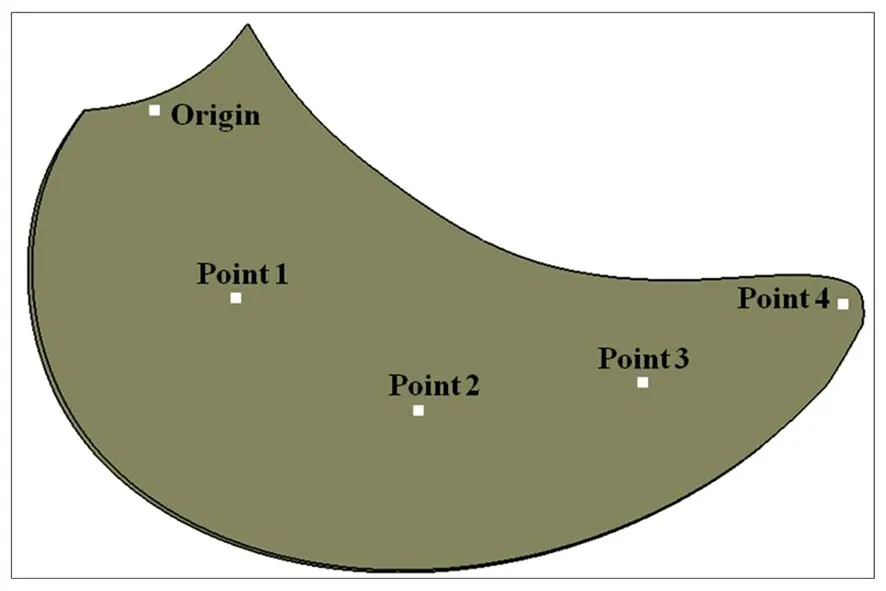
图11 叶面中面上的铺覆原点及4个标记点Fig.11 Origin and 4 markers on mid-surface of blade face
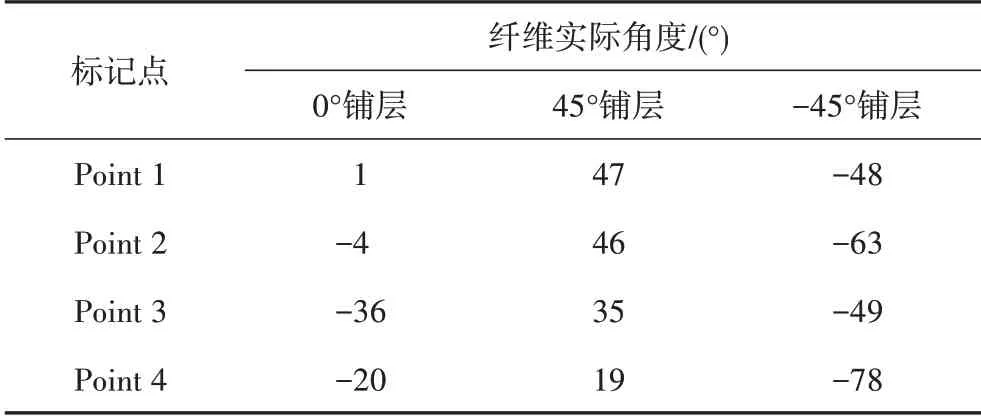
表5 标记点处3种铺层的纤维实际角度Tab.5 True fiber angles of 3 layers at the markers
3 结论
(1)复合材料螺旋桨叶片各处铺层均采用[0/45/0/-45]sn对称铺层时,不考虑纤维取向改变时叶片固有频率及均布压力载荷下最大变形的计算结果误差小于5%,热载荷下考虑真实纤维方向时的最大变形量约为不考虑真实纤维方向时变形量的2倍。
(2)0°方向的铺层在局部坐标系下的角度与原设定角度之间的偏差最大超过35°,45°方向的铺层最大角度偏差超过25°,-45°方向的铺层最大角度偏差超过30°。
(3)为了避免因纤维方向不准确导致计算误差,在进行复合材料螺旋桨叶片有限元分析时应基于铺覆后的真实纤维方向。
