初中数学中关于动点问题的试题探究
2020-03-25李亚亚

摘 要:动点问题是中考数学的高频考点,近几年中考试题中,以动点为基础的图形平移、旋转和剪拼问题频频出现在各类题型当中,同时,由于中考数学中动点问题题型灵活多样、难度大、综合性强,因此往往是命题者的宠儿。
关键词:素养;解题;特殊;模型
一、 中考试题中动态几何类问题的命题特征
动态几何知识模块具有很大的灵活性,熟悉这类题型的试题特征是提高解题效率、获得解题策略的重要途径。笔者选取甘肃省不同地区近5年的中考试题真题,通过对试题中动态几何部分知识的分类统计,归纳出中考试题的以下命题规律。
(一)知识点的分析
归纳历年中考试题中动态几何问题的考点分布,对于中考备考具有重要的指导意义。笔者在整理近5年省内各地区的中考试题后发现,在以往的试题中各知识点的分布中,试题中关于动态几何的知识点包括三类:其一,图形的变化性质、其二,锐角三角函数;其三,图形与坐标。其中,图形的变换包括图形的平移、对称与旋转、图形的相似、投影与三视图;三角函数主要考查了锐角三角函数和解直角三角形及其应用;图形与坐标则主要考查图形运动中对应的位置的变化。
新课标中动态几何知识模块也有比较详细的划分,同时,考纲中关于动态几何问题涉及的有三角形、四边形、图形的变化等相关知识。三角形相关知识点是其中的高频考点,比例多达28%,而四边形考查比例为11%。通过对考题的进一步统计与分析,笔者还发现面积公式、勾股定理、三角形的性质、三角形全等的判定或者相似性的证明是三角形相关题型中常考的点。图形的变化则考查了图形的平移、对称和旋转,图形旋转的考查频次最高,5年4考,对图形平移的考查有逐年弱化的趋势。
(二)试题类型分析
根据对动态几何问题的分类研究,以及真题中求解类型和变式升级讨论可知,求解类型的题目包括:求动点坐标、求函数表达式、猜想证明“最值”问题等题型。其中猜想证明类题目则包含证明三角形的全等、三角形的相似、线段的长度、三角形的角度等。“最值”问题包括面积的最值、线段最值等。求函数表达式,一方面涉及中学常见的基本函数,如一次函数、二次函数和反比例函数,另一方面还包括动态问题中与图形面积、线段最值等有关的函数关系。根据统计与分析还发现,甘肃省近五年试题中,动点坐标计算、函数关系式、猜想证明以及线段或面积的最值问题考查次数较多分别为13,7,7,10。尤其是猜想证明类题型最多,这类题目难度较大,且具有一定的区分度,容易拉开分值差距,失分最严重。
(三)试题特点的分析
中考数学试题一般具有以下两个显著特点:其一,基础性与梯度化相结合,其二,空间观点与推理论证并举。这样的试题特点也将贯穿于以后的中考试题当中,是任何命题人都参照执行的命题准则。
首先就第一点而言,一方面,基础性体现出基础教育的价值,梯度化重点突出了人才选拔。尽管省内各个地区对基础性题的考查比重是不完全一致的,但是总体上看来,各套试题对学生不可或缺的几何基本素养都进行了重点考查,如白银市2019年中考试题中第3题考查了简单组合图的三视图,同年的兰州卷选择题第15题则考查了反比例函数的几何性质等题目,都围绕着初中几何教学中最基本的概念、原理和规律进行考核,中等偏下难度的题目占到总分值的8成以上。另一方面,中考作為重要的选拔性考试,数学考试中的动态几何仍然保持着合理的梯次设置,这样的设置很好地贴合了不同学习能力学生的学习需求。
其次,各地区的中考试题中对学生应该具备的空间观点和推理论证能力都有不同程度的体现。如兰州卷选择题第3题考查了简单组合图的三视图,白银卷第5题考查了中心对称和轴对称的概念。
二、 动态几何问题的解题策略
在初中数学教学中,教师一定要明确,动态几何问题的解决一定是建立在大量的知识积累基础上的。在教学实践中,教师一方面要让学生熟悉常见的基本图形、常用的数学模型以及常用辅助性作图方法;另一方面,读图能力是中学几何教学的重要方面,要培养学生数形结合的意识,这是解决动态几何问题的重要思想方法。鉴于学生动态几何问题解题中的基本现状,笔者总结出以下对应策略。
(一)以不变应万变
变和不变总是相对而言的,要用辩证的思维看待数学问题。在动态几何问题中,当某些变量变化时,总有一些量是保持不变的。学生要认真地审题,从变化当中提取有效信息,找到隐含在变化当中的不变的量。同时要注意,获得不变的量往往可以通过对图形进行平移、旋转等变形后出现。
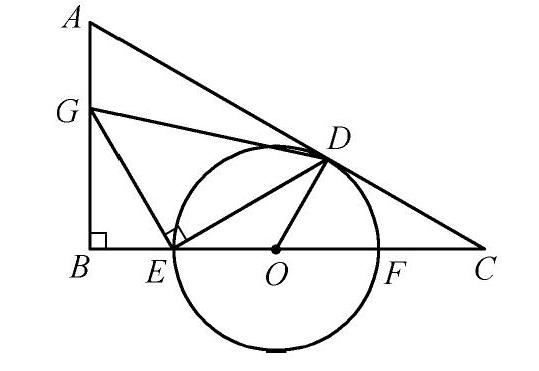
例1 如图,已知Rt△ABC中,∠B=90°,∠A=60°,AB=23cm,点O从C点出发,沿CB以每秒1cm的速度向B点方向运动,运动到B点时运动停止,当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与BC边所在直线相交于E、F两点,过E作EG⊥DE交直线AB于G,连结DG。
(1)求BC的长;
(2)若E与B不重合,问t为何值时,△BEG与△DEG相似?
解析:Rt△ABC中,∠B=90°,∠A=60°,AB=23。
AB∶BC∶AC=1∶3:2。
BC=3AB=3×23=6。
(2)OC=t,OD=t/2,DE=(3/2)×t。
BE=6-3t/2,GE=2BE=12-3t。
△BEG∽△DEG,则GE/DE=3。
或DE/GE=3。
(12-3t)=3t/2,24=9t,t=83。
或12-3t=12t,24=7t,t=247。
在类似的动态问题的解决中,学生一定要明确解题的关键,要抓住动态问题中不变的东西,用辩证的观点看待动和静之间的相互关系。要以动为突破口,将动态的变化转化为静态的可以解决的问题中来。
(二)以一般对特殊
数学解题的本质是实现未知问题向已知问题的转化。在中学试题中,动态几何的动线型问题的解题关键也常在于能否把特殊的问题转化为学生熟悉的数学情境中,用一般模型去处理特殊关系,最值问题更是如此。如以下问题中的最短距离的求解。
例2 一艘货轮位于海上的A点,P为灯塔,A此时处于灯塔P的南偏西60°的方位,当货轮朝东行驶20海里后到达点B,B在P的南偏西45°的某处,若货轮继续朝着正东行驶,问行驶过程中货轮与灯塔P的最短距离。(结果保留根号)
【考点】勾股定理的应用;方向角问题。
【分析】利用题意得到AE⊥PE,∠APE=60°,∠BPE=45°,AB=20,如图所示,在Rt△APE中,可以计算出
AE=3PE,再判断△PBE为等腰直角三角形得到BE=PE,然后通过AE-BE=AB计算出PE即可。
【解答】解:延长线段AB,然后作点P关于该延长线的垂线,相交于点E,如图,
由“垂线段最短”可知:PE的长就是轮船航行途中与灯塔P的最短距离,在Rt△PBE中,∠BPE=45°,∴BE=PE,在Rt△APE中,∠APE=60°,∴AE=3PE,
∴3PE-PE=20,
∴PE=203-1=103+10。
答:轮船航行的最短距离是(103+10)海里。
由此可见,中考试题当中涉及动点问题的部分,多是围绕点、线和面之间的相对位置关系展开,学生在解题中一定要找准变量之间的特殊关系,建立它们之间的可以用函数表示的一般模型。如果能把这样特殊的数学情境用具体的函数表示出来,那么,抽象的几何关系就可以用学生熟悉的函数来解决。最大值、最小值等最值问题就成功转化为一个数学中的函数问题。通过将特殊问题一般化,学生在解题中就可以找到该类问题普适性的解题方法,从而將抽象的几何动点问题转化为静态的、自己熟悉的问题情境中来。
(三)以静态对运动
数学当中的所有动态过程都是由一个一个的静态瞬间组成的,动态几何问题的解题本质也是借用转化思想,将动态过程中的点、线和面分解成一个一个相对独立的瞬间,然后从中找到相对“静止”的背后的运动规律或者特殊的静态图形,然后以此为基础进一步证明求解。
例3 如图所示,在平面直角坐标系中,函数
y=kx(k>0)的图像上有P、Q两点,P、Q坐标分别为P(1,4)、Q(m,n)。当m>1时,分别作过点P关于x轴、y轴的垂线于A、B两点;过点Q分别作x轴、y轴的垂线于C、D两点,DQ与AP相交于点E,求当m增大时,四边形EQCA的面积( )
A. 增大
B. 减小
C. 先减小后增大
D. 先增大后减小
【分析】该动点问题可以转换为函数问题,然后利用函数的性质求四边形面积的递变规律,这样就可以成功地将几何问题转化为函数问题。
【解答】解:AC=m-1,CQ=n,
则S四边形ACQE=AC·CQ=(m-1)n=m·n-n。
∵P(1,4)、Q(m,n)在函数y=kx(x>0)的图像上,
∴m·n=k=4(常数)。
∴S四边形ACQE=AC·CQ=4-n,
∵当m>1时,n随m的增大而减小,
∴S四边形ACQE=4-n随m的增大而增大。
故选:A。
【点评】本题考查了反比例函数的性质以及矩形的面积的计算,m增大时四边形的面积大小也在不断地变化,要证明面积的大小变化规律时,将特殊的数学情境转化为函数关系,用函数表示四边形ACQE的面积,通过对函数性质的讨论就可以判定该四边形面积的变化情况。
总之,教师在动点问题的备考中,一定要循序渐进,夯实基础,注重思维发展的层次性要求;同时,要不断地研究试题,归纳解题方法,提高解题技巧。只有这样,才能真正服务于教学实践,提高学生学业成绩。
参考文献:
[1]孙远琴,林泽飞.初中几何教学中的数学情境与提出问题:“平行四边形性质的应用”教学案例[J].数学教育学报,2011(4):91-93.
[2]何国伟,杨德焱.一道中考几何计算题解法的探究与启示[J].中国数学教育(5):16-18.
[3]马先龙.构造图形打开解中考几何最值问题的突破口[J].中学数学杂志,2014(10):52-53.
[4]霍晋兰.解析中考动态几何问题[J].数理化学习:初中版,2007(6):21-23.
作者简介:李亚亚,甘肃省白银市,甘肃省会宁县八里湾乡教育管理中心百户小学。
