基于AHP的既有预应力混凝土空心板梁承载能力评价

王亚飞，王行耐*，王永利，彭霞，韩亮亮

1.山东交通学院 交通土建工程学院，山东济南 25000；2.威海市公路事业发展中心，山东威海 264200

0 引言

随着经济水平的提高，截止到2018年底，我国已建成公路桥梁85.15万座。四级及以上等级公路里程中，高速公路里程占比逐年稳步提高，高速公路主要运输装备类型逐渐由客运转为货运[1]，我国交通运输结构渐渐向高速、重载的现代化运输结构过渡[2]，部分高速公路的原设计车道运输能力已远不能满足现代化的运输需求。

在对公路桥梁进行加宽或改造时，按文献[3]定量化应用检测结果，客观评估桥梁承载能力恶化状况,评定结果决定旧桥是否需要拆除及旧梁拆除后梁板二次利用的范围。这种计算方法对环境条件良好的桥梁来说，承载能力恶化系数偏大，将会降低桥梁运输能力的利用率，增加旧桥改、扩建和加固费用。文献[4]论述了国内外对于服役桥梁可靠性评估的进展，指出我国可靠性评估的局限性；文献[5]论述了层次分析(analytic hierarchy process，AHP)法在承载能力检算系数上的应用；文献[6]论述了现有承载能力评定的方式，分析各自的优缺点；文献[7]总结实际案例，验证了蒙特卡罗法在工程评定中的适用性；文献[8]论述了模糊综合评定理论有很高的保证率；文献[9-12]论述了如何在不确定层次分析下确定桥梁评估的最优指标权重。现有评定方法未考虑裂缝对承载能力恶化的影响[13]，造成目标因素过少、权重值偏大；分析方法单一，层次分析法[14]、模糊分析法[15-16]、熵权法[17-19]、神经网络法[20-21]等方法各有侧重点，综合运用多种方法可使结果更准确。

本文对5座建成时间、环境条件、交通流量均相同的高速桥梁进行承载能力研究，基于AHP法并参考熵权法理论，将熵权改为去除最大值和最小值后取平均的方法融入AHP法中；参考遗传分析法，引入隶属度函数公式，以达到准确评估旧梁承载能力恶化系数的目标。在对桥梁进行外观检测后，对比单梁荷载试验推定的实际结果、规范推定结果和分级模糊理论计算结果，以期寻找最接近实际承载能力的评价方法，可为高速公路改、扩建过程中旧梁承载能力的评价提供参考。

1 旧桥承载能力恶化状况综合评价方法

1.1 AHP法评估指标分层及修正

图1 恶化状况评定标度分层模型

基于模糊综合评估法，对恶化状况评定标度E进行重新取值、归类，将恶化状况分为目标层E(恶化状况评定标度)、准则层A(裂缝、钢筋、混凝土)、指标层B(受力裂缝、锈蚀裂缝、锈蚀电位、护层厚度、缺损状况、电阻率、碳化状况、氯离子质量分数、混凝土强度等)[22]，修正后的层次模型如图1所示。

1.2 AHP判断矩阵

采用1～9标度法建立判断矩阵，矩阵中的Bij表示同一分层中i比j的重要程度，判断标度如表1所示。

表1 Bij判断标度及取值范围

根据表1的定义及标度，基于目标层E、准则层A、指标层B三者之间的从属关系，对E、A1、A2、A3中的因素进行两两比较，得判断矩阵：

式中：Aij表示Ai对Aj的重要程度，其余矩阵中的元素符号同理。

为进行一致性检验，计算判断矩阵U的特征值及特征向量。即对于判断矩阵U，应满足

Uω=ηmaxω，

式中：ηmax为矩阵U的最大特征值；ω为对应的特征向量，即相应参数的权重。

采用和法计算归一化的特征向量[23]，将U每一列归一化：

(1)

式中n为判断矩阵的阶数。

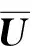
(2)

特征向量归一化，得

(3)

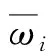
可得权重系数矩阵

计算最大特征值

(4)

1.3 一致性检验

采用AHP法时，若判断矩阵为非一致性矩阵，则权重系数无法保证其合理性。因此计算得到权重系数后，需要检验权重系数的合理性，即检验判断矩阵的一致性。

一致性指标

(5)

一致性比率

LCR=NCI/RRI,

(6)

表2 RRI指标计算结果

式中：RRI为重复计算1000次的平均随机一致性指标，1～5阶RRI如表2所示。

当LCR<0.1时，该判断矩阵为一致性矩阵；当LCR>0.1时，需调整判断矩阵，直到LCR<0.1，满足一致性检验要求。

1.4 配筋混凝土构件恶化状况评估集

根据文献[3]中各等级之间的评定标度及实桥检测的经验，建立各影响因素的评定标准。将B1～B9划分为5个等级，5分为情况最差，1分为情况最优，按此评定标准建立评估集

V={v1,v2,v3,v4,v5}={5,4,3,2,1}。

(7)

1.5 多级模糊综合评估

分级模糊理论计算的关键为确定准则层A、指标层B的隶属度，而隶属度为定量指标，定量指标的关键为划分定量指标的等级标准是否准确。隶属度采用专家评价法与隶属度函数结合的方式确定。

1)专家赋分。选取10名资深桥梁检测专家对图1指标层各因素按式(7)赋分，赋分后去掉一个最大值和一个最小值，将其他赋分结果的平均值作为相应因素的得分。

2)指标层评估矩阵。对准则层A1～A3的各个指标层因素进行评估并建立各自的评估矩阵

(8)

式中rij为第i个影响因素对第j个评定标度的隶属度。

3)隶属度函数。采用F分布中的降半阶梯法得最小最优解，确定vj级隶属度函数

(9)

确定vj+1级隶属度函数

(10)

4)二级模糊综合评估。采用模糊矩阵、合成算子、权向量三者相互运算的模式。

KAm=WB⊙Am,m=1，2，3。

(11)

式中：⊙为模糊算子，如表3所示；KAm为Am的模糊评价结果;WB为准则层Am所包含因素得权重构成得单行矩阵。

表3 模糊算子分类

分析模糊算子及其适用环境，选用M(•，⨁)为模糊算子，即：

(12)

5)一级模糊综合评估。把A1、A2、A3的模糊矩阵运算结果作为一级模糊综合评估的因素集KE，对因素集的权重矩阵WA与相应的判断矩阵Am作模糊运算，即：

KE=WA⊙Am

(13)

6)恶化状况评定标度E最终评价。用加权平均的原则对二级模糊综合评估结果KA进行计算，其计算结果就是恶化状况评定标度E的分级模糊理论综合评价值，即：

(14)

式中n为二级分层因素的个数。

2 应用实例

以山东省境内某高速公路5座20 a以上的空心板桥梁检测资料为依据，其跨境分别为6、8、10、13、16 m。5座桥梁外观完好，地处寒冷地区[24]，属于干、湿交替冻无侵蚀性介质环境。冬季干旱少雨雪，其平均降水量为全年的5%左右[25]；该桥设计荷载为汽车-超20级，挂车-120级。

2.1 评价指标及权重

1)建立判断矩阵。对6 m旧桥空心板承载能力恶化评定标度E中的各项指标打分，建立目标层E中因素A1～A3的判断矩阵

建立准则层A1中因素B1、B2的判断矩阵

建立准则层A2中因素B3、B4的判断矩阵

建立准则层A3中因素B5、B6、B7、B8、B9的判断矩阵

2)由式(1)～(3)对判断矩阵进行归一化处理，得相应的特征向量。

由式(1)对UA3矩阵每一列进行归一化处理，得

由式(2)对UA3每行求和处理，得向量

ωUA3=(1.994 0.245 0.822 0.822 0.059)T。

3)由式(3)对ωUA3归一化处理，得特征向量

4)由式(4)计算最大特征值ηUA3，即

5)利用式(5)(6)对ωUA3i权重进行一致性检验，即

NCIA3=0.041,LCRA3=0.021<0.1,

证明权重系数合理，判断矩阵有较强的一致性。同理可验证ωUEi、ωUA1i、ωUA2i均满足一致性要求。

评价指标及各层对应权重结果如表4所示。

表4 评价指标对应权重

2.2 多级模糊综合评价

1)10位专家对6 m空心板梁各因素赋分，舍弃最大值和最小值后取平均值，如表5所示。

表5 6 m空心板梁恶化评定标度各因素打分结果

2)利用式(7)～(10)建立6 m空心板梁准则层(A3)下指标层的评估矩阵RA3，即：

3)利用式(11)(12)计算准则层(A3)的KB，将指标层各因素的KB组合成准则层模糊综合评判矩阵KA3，即：

同理可得矩阵KA1、KA2，即

4)将KA1、KA2、KA3组合成目标层因素得模糊综合判断矩阵

同理利用(13)得KE，即

5)利用式(14)得6 m空心板梁恶化状况评定标度E的分级模糊理论综合评价结果，即E=1.725，同理可得8、10、13、16m空心板梁恶化状况评定标度E，如表6所示。

表6 空心板恶化状况评定标度

3 试验段旧桥承载能力评定

3.1 试验段旧桥各影响因素系数的确定

承载能力检算系数Z1如表7所示。构件恶化状况评定标度E及承载能力恶化系数ξe如表8所示。截面折减系数ξc、ξs如表9所示。

表7 各空心板技术状况评定计算结果

表8 构件恶化状况评定标度及承载能力恶化系数

表9 截面折减系数

3.2 承载能力极限状态理论值的确定

3.2.1 旧桥梁断面尺寸

查阅相关设计说明，混凝土等级为C40，横截面一般构造如图2所示(图中单位为cm)。

a) 6 m b) 8、10 m

c) 13 m d) 16 m图2 6、8、10、13、16 m细部构造图

3.2.2 承载能力极限状态计算结果

截面承载能力极限状态的理论计算结果如表10所示。

表10 承载能力恶化系数及极限承载能力结果对比

由表10可知，规范计算结果与实际承载能力的误差小于2.5%，AHP法计算结果与实际承载能力的误差小于1.0%。两种方法的计算结果都在桥梁实际承载能力允许误差范围内。

4 结语

基于旧桥改、扩建工程，对实际工程项目中的5座桥进行承载能力恶化状况评估，采用AHP法并参考熵权法理论，进行多级模糊综合评估。将旧桥恶化状况分为目标层、准则层、指标层，对各指标因素建立判断矩阵，确定评价指标及权重，进行分级模糊评价。确定旧桥各影响因素的检算系数，建立有限元模型计算理论承载能力极限状态，最终确定规范法和AHP法的计算结果与实际承载能力的误差。

计算结果表明，两种方法的计算结果都在桥梁的实际承载能力范围内。规范方法计算的承载能力恶化系数偏大、桥梁承载能力评估偏低；AHP法计算的承载能力恶化系数更加准确，桥梁承载能力更接近真实水平；AHP法将裂缝纳入到评价因素中，使评价结果更加科学。该AHP法对今后承载能力恶化系数算法的改进有一定参考意义。