双层金属波纹管抗冲击性能研究

王洪斌1，刘永刚，吴 舟，李冬颖

(1.中国一拖集团有限公司，河南洛阳 471003；2.河南科技大学 机电工程学院，河南洛阳 471003)

0 引言

双层波纹管是通过将两个单层波纹管套合在一起形成的，其位移补偿能力更高，具有高强度和更好的柔韧度，是舰船管道系统中的一个重要部件。随着舰船的隐身技术的要求越来越高，降低舰船管道系统的噪声非常重要。管道噪声是舰船机械噪声的主要来源之一，波纹管作为管道系统中主要的减振降噪部件，对其隔振、隔声性能有很高的要求。此外，舰船还可能遭遇深水爆炸和撞击等情况，这时船体会受到一个瞬态冲击波[4-7]，并传递给管道系统，管道系统受到冲击后常常会因为变形过大而造成损坏，从而导致舰船的动力系统和液压系统管道丧失功能，使舰船失去动力和战斗力。波纹管作为管道系统位移补偿和吸能的重要构件，对其在冲击载荷作用下的动态响应进行研究，为提高波纹管的抗冲击性能设计，对提高舰船的寿命和战斗力起着至关重要的作用。

陈海龙等[4]利用DDAM法和时域法相结合的方法，在频域和时域上对船用典型动力设备进行了抗冲击分析，通过分析结果表明，船用设备的自身特征和载荷施加的方向对冲击响应的影响较大；耿盼盼等[5]用ANSYS软件在时域上分别从垂向、横向和纵向对舰用燃气轮机施加正负三角冲击波，得到了其冲击动态响应特性，并根据支架的冲击能力对其进行了优化;姜忠涛等[7]基于ABAQUS软件中的耦合欧拉-拉格朗日算法，模拟水下爆炸气泡射流载荷对船体外板的冲击过程，对射流的压力特性和速度分布，以及射流冲击引起的结构剪应力分布进行仿真分析；Kim等[8]利用三维有限元的方法分析了波纹管的振动模式和固有频率，结果表明低频振动导致了波纹管的应力不均匀分布;朱建峰[9]利用ADINA软件对高阻尼多层波纹管的轴向等效刚度进行了研究，并分析了波根外径、波距、壁厚和夹层阻尼材料对其轴向刚度的影响;曾诚等[10]用大质量法对建立的橡胶隔振器模型施加冲击脉冲，然后采用锤落式冲击试验法对橡胶隔振器进行动态冲击试验，并用半正弦波作为冲击输入条件，得到了不同工况下的冲击响应曲线,试验值和数值分析基本吻合;刘永刚等[11-12]采用有限元和试验结合的方法，对含夹层阻尼波纹管进行了力学性能研究;Wei等[13]针对金属波纹管成型工艺的缺点，提出一种水射流成型技术，利用试验获得了波纹管厚度控制的工艺;Prasanna等[14]根据膨胀节制造协会标准，采用试验和有限元法分析了设计参数与静态力学性能的关系，结果表明壁厚对波纹管静态力学性能影响比较大，并对设计参数进行优化;贺世忠等[15]以膨胀管式吸能元件为研究对象，利用全自动电液伺服压力机和大型落锤冲击试验机，研究了壁厚、锥头外径、冲击速度这三个参数对吸能元件吸能特性的影响规律。

近几年来，国内外学者对波纹管刚度、阻尼、振动性能和成型工艺等进行了一系列的研究工作，而对波纹管的抗冲击性能方面的研究很少见，国内还没有舰船管道系统的冲击试验的规范和标准[6]。文中以双层金属波纹管为研究对象，应用有限元软件ANSYS，采用瞬态动力学分析法对波纹管进行冲击性能分析，并对同型号波纹管进行抗冲击试验研究。

1 冲击响应分析

1.1 有限元模型

双层金属波纹管的剖面结构见图1。公称直径DN=1 500 mm，波高h=60 mm，圆弧半径R=14.25 mm，波距W=65 mm，壁厚s=2 mm，波数为6。材料为304不锈钢。

图1 双层波纹管的几何剖面结构示意

在管道系统中，波纹管通过两端的法兰盘连接管道系统。根据波纹管的结构特征，建立波纹管有限元模型，采用3个假设：(1)波纹管两层之间黏接性好，且各向同性；(2)壁厚分布均匀，发生变形时各层之间无相对滑移；(3)将法兰盘简化处理，用质量单元Mass 21直接替代法兰盘的质量，并与波纹管建立刚性连接。利用Proe软件建立波纹管的三维模型，将建好的波纹管三维模型通过无缝对接功能导入到Workbench中。波纹管属于薄壁结构，在ANSYS软件中，8节点Shell 93单元具有任意的空间各向异性，具备塑性、应力钢化和大变形能力，因此选用Shell 93单元建立波纹管金属壁的有限元模型。波纹管层间属于面面接触，接触面和目标面都是柔性的，所以在设置接触面时用Targe 170,Conta 174,Conta 175接触单元来建立绑定接触，在分析中会自动生成所需的接触对。由于波纹管是不规则的结构，因此采取映射法合理地划分壳体单元网格，节点数为53 000，单元数17 400，波纹管有限元模型见图2。边界条件设定波纹管一端为自由端，另一端为固定端约束。

图2 有限元模型

首先进行模态分析，获得波纹管前5阶模态频率和模态振型，第一阶模态振型见图3。

翻译活动存在于生活的方方面面，无论是电视或杂志广告、药品介绍，或是街头标语，但由于译者水平的参差不齐，出现了大量质量低劣的译文。其中的原因除了译者自身水平不足之外，最重要的原因还是在于译者的译者伦理意识的缺失。商务英语翻译和其他翻译不同，需要更多的兼顾顾客和译者之间的关系，在满足顾客或委托人意愿的同时也要遵循作为一个译者的基本操守。

图3 一阶的模态振型图

利用模态频率和单元动能，根据模态质量公式，得到波纹管轴向模态质量为209.844 kg，横向模态质量为43.89 kg。

1.2 冲击信号的设定

管道系统中冲击载荷非常复杂，无法准确得到冲击力的波形。根据潜艇核动力装置阀用多层金属波纹管规范(GJB 5323—2004)和冲击安全性-联邦德国国防军建造规范(BV043—85)可知，常用的冲击波形有三角波/半正弦波、双重三角波和双重正弦波等[4-5]。利用典型的三折线冲击谱的参数和波纹管的模态质量，可以计算得到冲击谱的谱位移D0=0.067 m，轴向冲击力的谱速度V0=2.93 m/s，谱加速度A0=648.5 m/s2；横向冲击力的谱速度V0=1.21 m/s，谱加速度A0=271.1 m/s2。

本文采用等面积的双重正弦波作为冲击信号，正弦波谱如图4所示。实践中，冲击信号一般根据三折线冲击谱(SAS)，利用以下公式进行转化：

A2=0.5A0

(1)

(2)

(3)

(4)

(5)

式中A2——第1个波的加速度幅值，m/s2；

V1——第1个波的速度，m/s；

V2——第2个波的速度，m/s；

t1——第1个波的持续时间，s；

t2——第2个波的持续时间，s；

A4——第2个波的加速度幅值，m/s2。

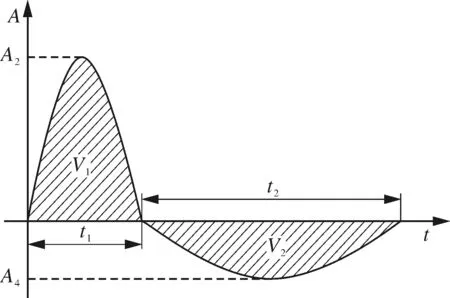
图4 双重正弦波谱

1.3 有限元分析

分别在双层金属波纹管的轴向和横向加载上述冲击信号，对波纹管进行瞬态动力学分析。轴向冲击信号垂直加载在自由端面的圆心处，图5为轴向冲击响应曲线。可以看出，最大加速度为143.5 m/s2，轴向最大冲击位移为8.6 mm。加速度响应曲线和位移响应曲线都是随时间的变化上下非对称振荡，轮廓线一致、均呈现逐渐减小的趋势，变化比较平缓，没有明显突变。说明波纹管没有发生结构性损坏。

(a)加速度 (b)位移

图5 轴向冲击响应曲线

横向冲击信号加载在自由端面的圆周上，沿着端面上作用点的横向，指向圆心。图6示出横向冲击响应曲线。可以看出，最大加速度为134.8 m/s2，横向最大冲击位移为1.89 mm，响应曲线变化比较平缓，没有明显突变。说明波纹管没有发生结构性损坏。

(a)加速度 (b)位移

图6 横向冲击响应曲线

2 试验研究

波纹管冲击试验采用落锤法，冲击激励信号有冲击速度法和脉冲波形法两种。为了更加有效地模拟波纹管的冲击环境，选用脉冲波形法中的半正弦波作为冲击激励信号，它的主要参数是脉冲峰值和脉宽。试验过程中，通过调整重锤的高度来改变冲击信号的脉冲峰值和脉宽。冲击试验系统由波纹管、重锤、横向冲击架、波形发生器、信号处理系统等组成。冲击试验系统原理见图7。

试验对象是同型带法兰盘的双层金属波纹管。信号处理系统包括：BK加速度传感器、BK电荷放大器、信号处理仪、电脑等。主要试验设备情况见表1。

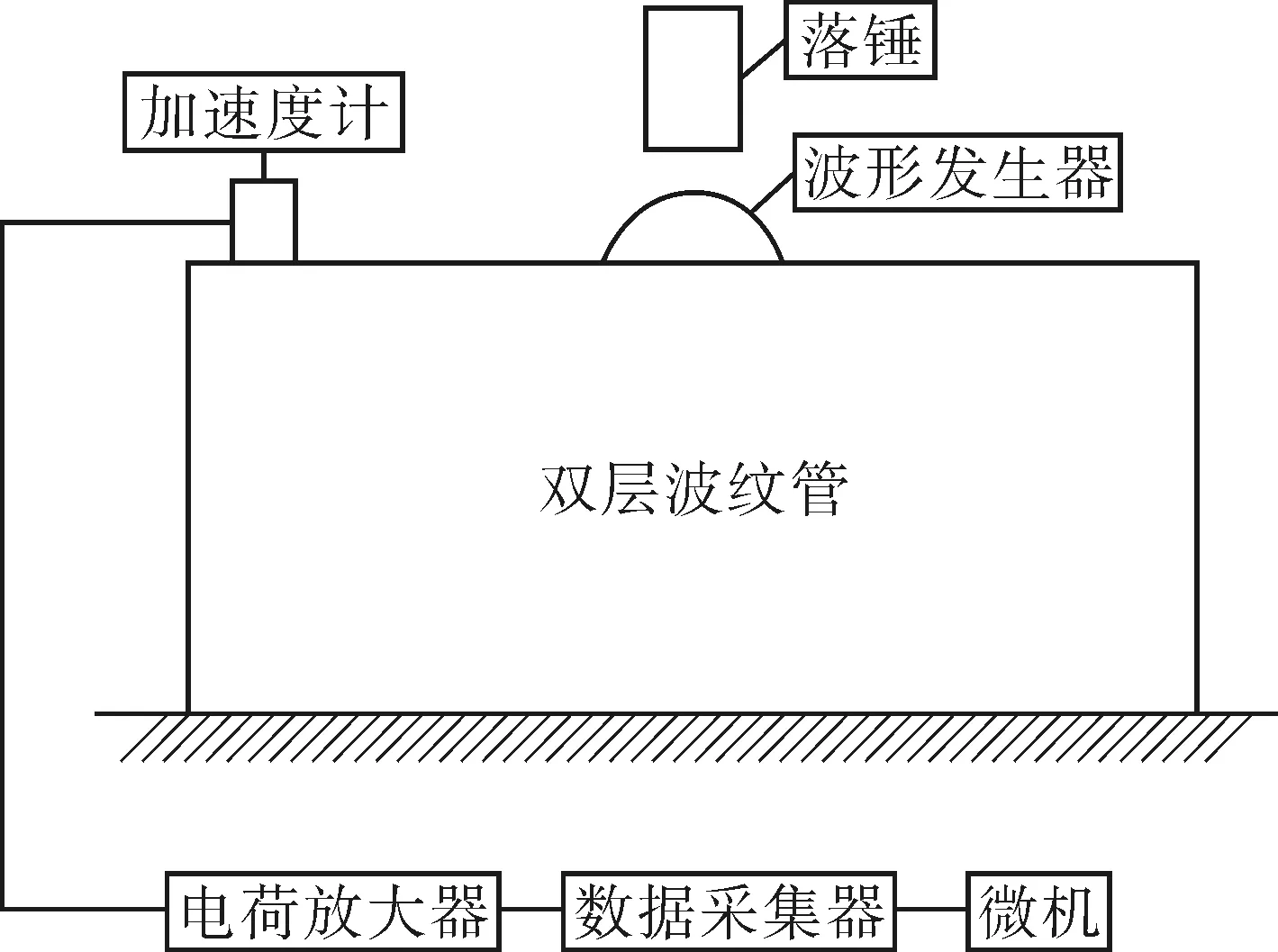
图7 冲击试验原理

表1冲击试验设备

设备名称型号生产厂家加速度传感器BK4371丹麦BK电荷放大器BK2635丹麦BK数据采集系统PCM3000河南科技大学电脑IBMIntel波形发生器(半正弦波)6 ms脉宽莱伯通试验设备有限公司冲击架自制

2.1 横向冲击试验

横向冲击试验系统见图8。波纹管的下端用地脚螺栓连接在地基上，在重锤冲击的瞬间，除了大量的动能被波纹管吸收，地基吸收了剩余的能量，这样使得波纹管受力均匀，保证波纹管不会在冲击力作用下跑偏。横向冲击架主要支撑波纹管装置，在试验过程中保持波纹管的轴向稳定性。并且冲击架具有引导重锤沿着横向垂直冲击在波纹管侧面的波形发生器上、限制波纹管发生轴向偏移(只能沿着横向运动)、检测波纹管横向位移等功能 。

图8 横向冲击试验系统

当重锤冲击在波形发生器上时，波形发生器给波纹管施加正弦冲击信号。横向冲击信号脉宽为2 ms，最大冲击速度为1.2 m/s。波纹管横向冲击响应加速度曲线见图9。响应开始后，加速度经历了大约2.6 ms，完成了第1个半正弦波形，到达最大峰值140.6 m/s2。通过横向冲击试验，检查到波纹管沿横向最大位移为2 mm后，可以恢复到原始位置，经过检测未发现波纹管有结构性损坏。冲击响应曲线上下波动不稳定，是因为重锤在完成第一次冲击后，跟随波纹管振动过程中，有时贴在波纹管上、有时分离，现场试验时，发出“砰砰”的连续冲击声。

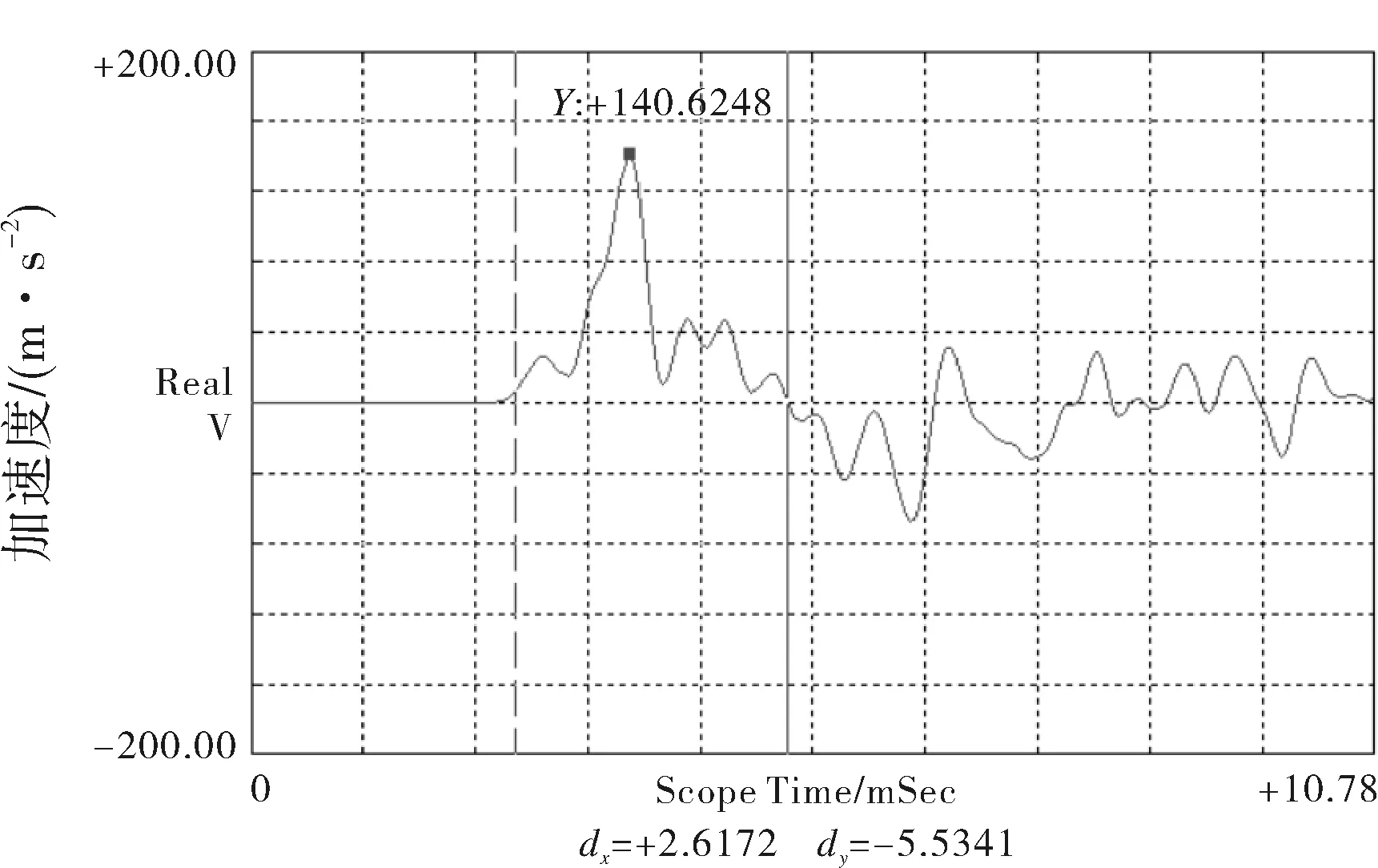
图9 横向冲击响应加速度曲线

2.2 轴向冲击试验

轴向冲击试验系统见图10。轴向冲击架保持波纹管横向稳定性，引导重锤沿波纹管中轴线垂直作用在波形发生器上，并均匀作用在法兰盘。调整重锤的高度，轴向冲击信号脉宽4 ms，最大冲击速度3 m/s。

图10 轴向冲击试验系统

图11 轴向冲击响应加速度曲线

重锤自由落体撞击在正弦波形发生器上，波纹管轴向冲击响应加速度曲线见图11。轴向冲击响应加速度曲线和横向冲击响应加速度曲线的变化趋势基本一致。加速度曲线表现出上下振荡并不断衰减的趋势，冲击开始的瞬间加速度几乎为零，反应十分微弱，随后加速度随着时间的增加而不断地增大。冲击响应发生后，在t=3.9 ms时，加速度达到了最大峰值148.6 m/s2，然后又随着时间的增加而减小。通过试验还发现，波纹管沿轴向变形到达最大位移(轴向9 mm)后，可以恢复到原始位置，经过检测未发现波纹管有结构性损坏。

2.3 结果分析

有限元分析和冲击试验结果见表2。可以看出，结果误差最大为5.5%。造成误差的因素有很多，如有限元模型简化、网格不够精细等。试验过程中的误差主要包括：重锤第一次冲击后，不能同波纹管有效分离，存在多次冲击现象；冲击台架的制造精度问题，造成冲击力不能准确沿着波纹管轴向和横向作用等因素。

表2 仿真值和试验值的比较

根据设计要求,该波纹管的轴向冲击许可位移为11 mm，横向冲击许可位移为3.3 mm。经过分析和试验,证明了波纹管的冲击性能满足设计要求，分析和试验的误差能够满足实际工程应用的需要；表明采用有限元软件对双层金属波纹管仿真结果是正确可靠的，采用瞬态动力学法在时域上对波纹管进行抗冲击动态分析是可行的。

3 结论

以双层金属波纹管为研究对象，基于ANSYS软件，采用瞬态动力学分析法，分析了波纹管轴向和横向的冲击响应，建立冲击试验平台，研究了在轴向和横向对波纹管的抗冲击响应，具体如下。

(1)建立有限元模型，进行模态分析，得到波纹管前5阶模态频率和阵型，计算得到轴向和横向模态质量。

(2)利用三折线冲击谱，根据波纹管的模态质量，建立轴向和横向双重正弦冲击谱。

(3)利用有限元模型，进行瞬态动力学分析，分析波纹管轴向和横向冲击响应。

(4)根据同型号波纹管的特点，建立冲击试验平台，研究了波纹管轴向和横向的冲击响应。轴向最大加速度的数值分析和试验结果的误差为3.4%，横向最大加速度的数值分析和试验结果误差为4.1%；作为参考，轴向最大位移的数值分析和试验结果的误差为4.4%，横向最大位移的数值分析和试验结果的误差为5.5%。数值分析和试验结果基本一致，说明该冲击分析方法准确有效，可以在同系列波纹管抗冲击性能研究中推广应用。