一种直接利用连续时间非周期信号的频谱计算相应周期序列的频谱的方法*
2020-03-25陈绍荣陈柏良薛在阳
陈绍荣,陈柏良,何 健,薛在阳
(1.陆军工程大学通信士官学校,重庆 400035;2.深圳市惟新科技股份有限公司,广州 深圳 518000;3.军委装备发展部军事代表局驻成都地区军事代表室,四川 成都 610041;4.奥特斯科技(重庆)有限公司,重庆 401133)
0 引 言
在国内外《信号与系统》著作[1-2]中,对连续时间非周期信号、非周期序列和周期序列的频谱,依据各自的定义,研究其性质、定理,一般仅研究了两种信号频谱之间的关系。基于《信号与系统》著作[3]和《数字信号处理》著作[4],本文利用函数逼近冲激函数时,其曲线下的面积保持不变的特性,证明了周期冲激信号的频谱具有离散性、谐波性和均匀性。以此为基础,导出了连续时间非周期信号频域分解的表达式及其频谱计算公式。然后分别导出了非周期序列的频域分解表达式及其频谱计算公式。最后不仅给出了基于连续时间非周期信号的频谱来计算相应周期序列的频谱的方法,而且还给出了基于连续时间非周期信号的频谱来计算相应周期序列的频谱的实例。
1 连续时间非周期信号的频谱

由式(1)可知,x(t)是周期为T0的连续时间周期信号,并且t=mT0(m为整数)时,将出现冲激函数Aδ(t-mT0),因此,由式(2)可以得到:
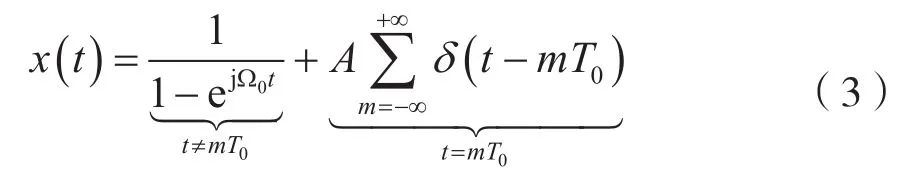
式中,第二项是第一项当t→mT0时的结果。考虑到函数逼近冲激函数时,其曲线下的面积具有保持不变的特性,若m=0,则冲激函数Aδ(t)的强度A为:

考虑到式(1)、式(3)、式(4)及单位冲激函数δ(t)为偶函数,则有:
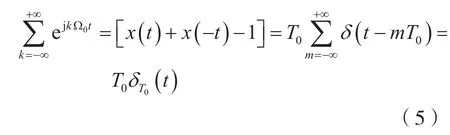
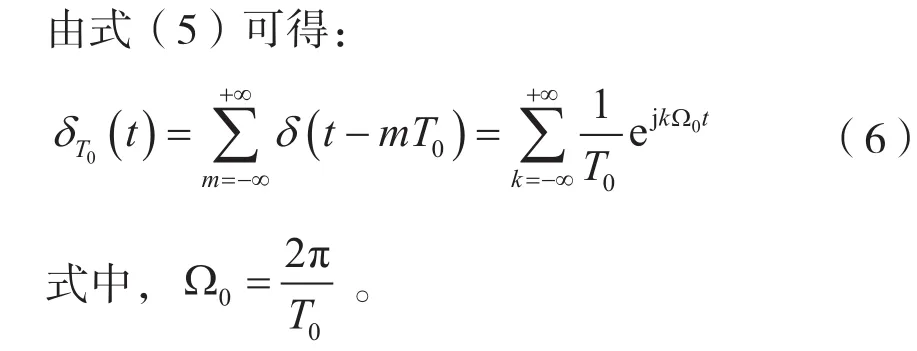
式(6)表明,周期冲激信号δT0(t)可以分解成无穷次谐波kΩ0(k=0,±1,±2,…)之和,并且各次谐波的幅度都为1/T0(均匀性)。由于在频域上角频率Ω取值不连续(离散性),按kΩ0(k=0,±1,±2,…)的方式取值(谐波性),因此,通常用X(kΩ0)表示周期冲激信号δT0(t)的频谱,即X(kΩ0)=1/T0。
考虑到式(1),则有:

考虑到式(7),则连续时间非周期信号xa(t)的频域分解可以表示为:

式中,称Xa(jΩ)为连续时间非周期信号xa(t)的频谱,并且,可以表示为:
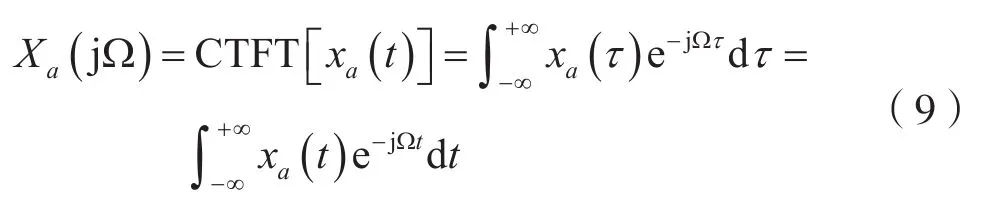
式(9)表明,连续时间非周期信号xa(t)的频谱Xa(jΩ)是频率Ω的连续函数。
若以等间隔T对连续时间非周期信号xa(t)进行抽样,则样值信号xs(t)可以表示为:
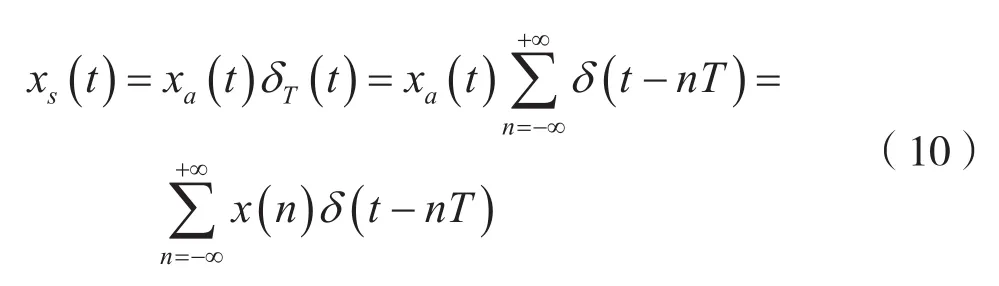
式中,x(n)=xa(nT),称x(n)为非周期序列。
考虑到式(9)、式(10)及式(6),则样值信X号xs(t)的频谱Xs(jΩ)可以表示为:

式(11)表明,时域上以等间隔T对连续时间非周期信号xa(t)进行抽样,得到了样值信号xs(t),则频域上以Ωs为周期对连续时间非周期信号xa(t)的频谱Xa(jΩ)做周期延拓,再除以T,就得到了样值信号 xs(t)的频谱 Xs(jΩ)。
2 非周期序列的频谱
考虑到式(8)及式(11),则非周期序列x(n)=xa(nT)的频域分解可以表示为:

式中,数字角频率ω=ΩT。X(ejω)称为非周期序列x(n)的频谱,并且,可以表示为:
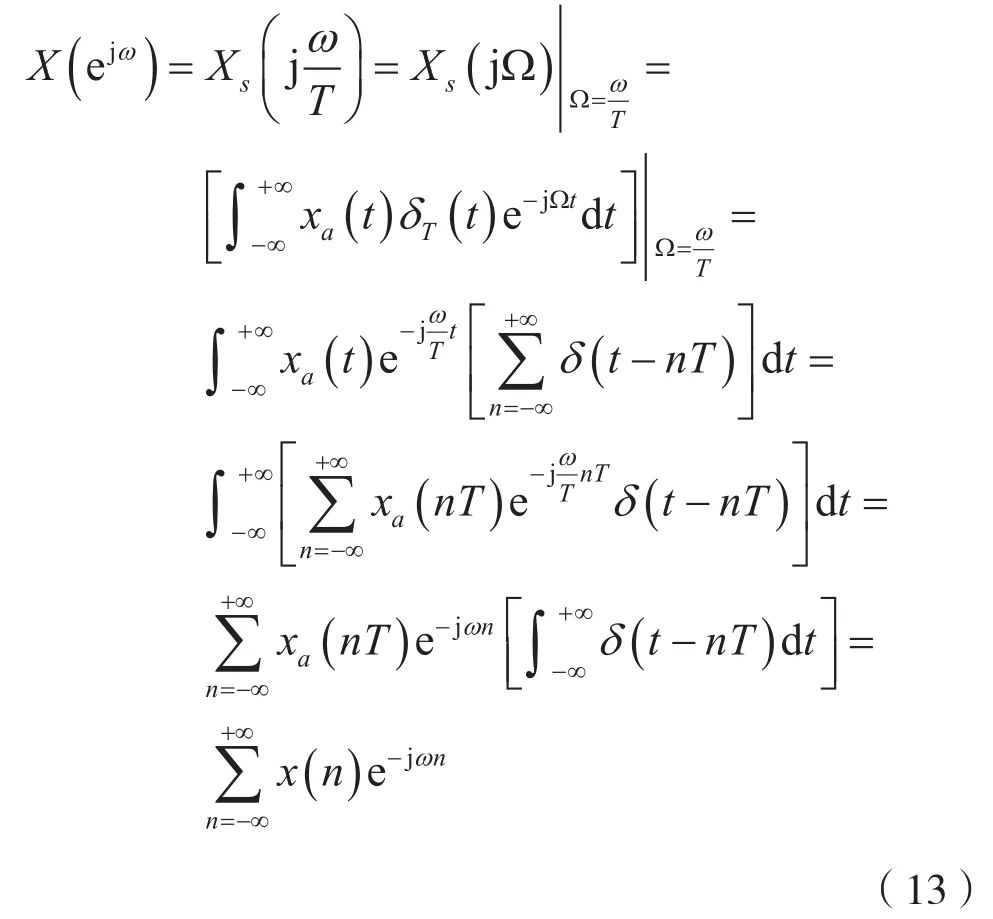
式(13)表明,非周期序列x(n)的频谱X(ejω)不仅是数字角频率ω的连续函数,而且是周期为2π的周期函数。
3 周期序列的频谱
考虑到式(6),即:

考虑到式(18)、式(12)、式(17)及周期函数在一周期内的积分与起点无关,则一个周期为N的周期序列x~(n)的频域分解可以表示为:

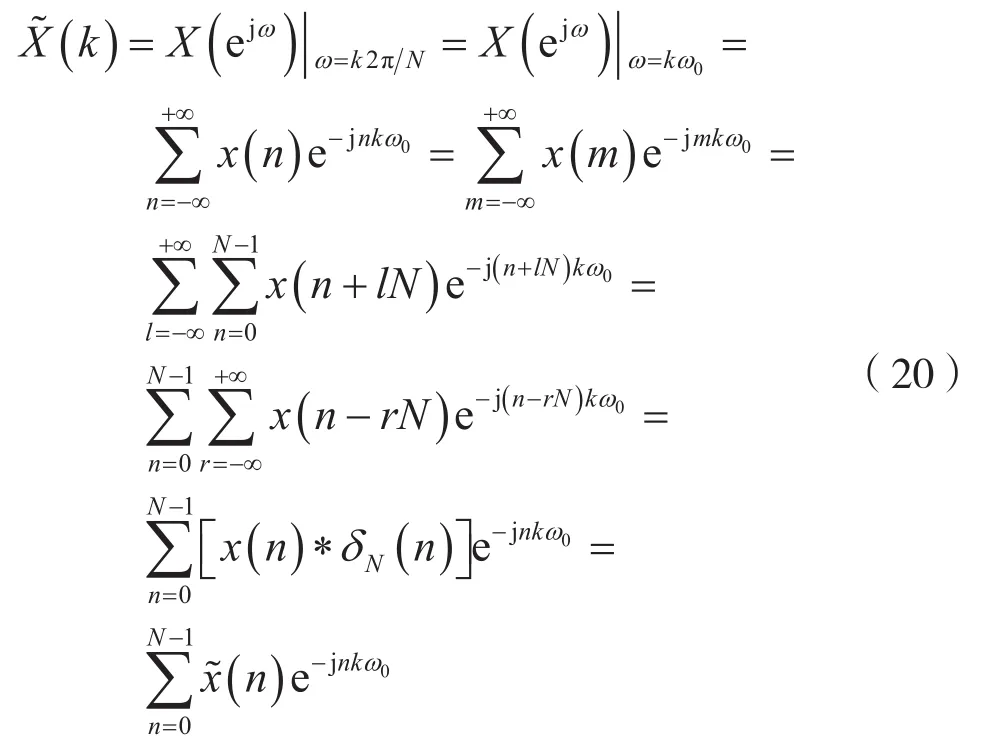
4 基于连续时间非周期信号的频谱计算相应周期序列的频谱
考虑到式(20)、式(13)及式(11),则有:
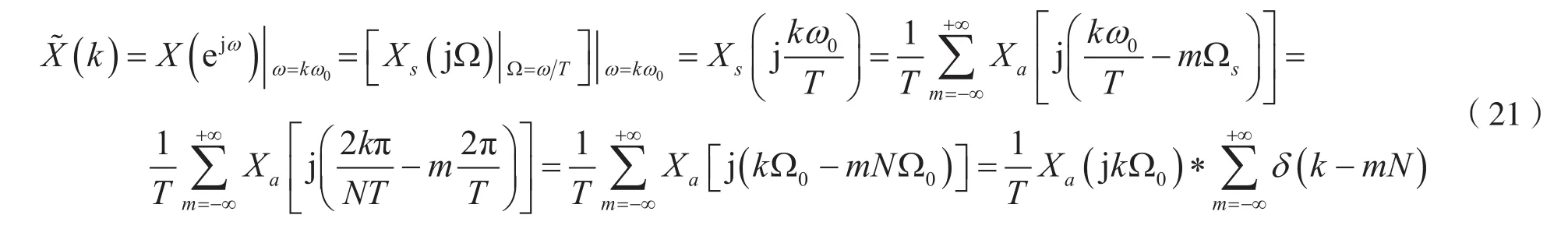
式(21)是直接利用连续时间信号xa(t)的频谱Xa(jΩ)来计算相应周期序列的频谱的依据。
(1)试直接利用连续时间信号xa(t)的频谱Xa(jΩ)计算相应周期序列的频谱
解:(1)考虑到
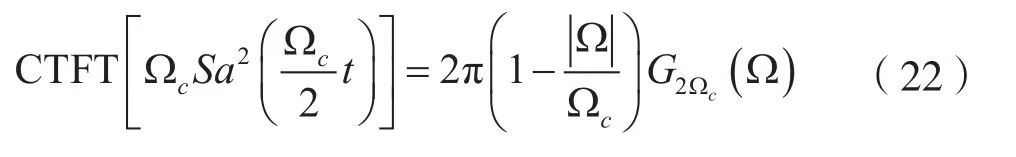
式 中,G2Ωc(Ω)=ε(Ω+Ωc)-ε(Ω-Ωc),ε(Ω)为 单 位阶跃函数。
在式(22)中,令Ωc=π/2,可得:

考虑到式(23),则连续时间非周期信号xa(t)的频谱为:

定义矩形窗:

式中,ε(k)为单位阶跃序列。
考虑到式(24)及式(25),则有:
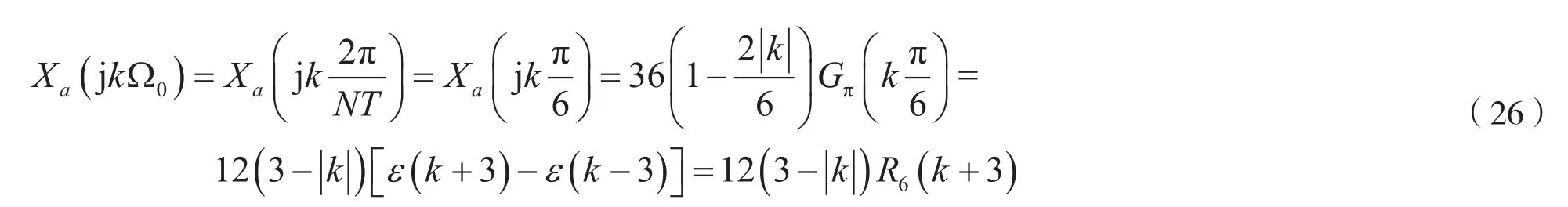


5 结 语
本文证明了周期冲激信号的频谱具有离散性、谐波性和均匀性。以此为基础,导出了连续时间非周期信号频域分解的表达式及其频谱计算公式。然后分别导出了非周期序列的频域分解表达式及其频谱计算公式。最后不仅给出了基于连续时间非周期信号的频谱来计算相应周期序列的频谱的方法,而且还给出了基于连续时间非周期信号的频谱来计算相应周期序列的频谱的实例。
