一种功率最小化的双层迭代子载波分配算法*
2020-03-25李孜恒
孟 超,李孜恒,戴 西,王 刚
(1.金陵科技学院 网络与通信工程学院,江苏 南京 211169;2.东南大学 移动通信国家重点实验室,江苏 南京 210096)
0 引 言
随着无线通信技术的快速发展,越来越多的用户选择无线传输的方式接入互联网。同时,随着物联网技术的发展,越来越多的设备接入互联网[1-2]。接入的用户和设备对网络的服务质量如传输速率、网络延迟等提出了更高要求[3-4]。由通信相关行业产生的能源消耗每年都在以极快的速度增长,因此无论是从降低运营成本还是从保护生态环境考虑,降低无线通信系统的能量消耗,提高能量的使用效率,已引起人们的广泛关注。
正交频分复用(Orthogonal Frequency Division Multiplex,OFDM)和多输入多输出(Multiple-Input Multiple-Output,MIMO)技术是第四代移动通信的关键物理层技术。OFDM技术可以有效对抗多径干扰,提高系统的频谱利用率[5-6]。文献[7]给出了一种关于子载波和功率联合分配算法,在利用注水算法使用户的最小速率满足要求后,对速率需求较大的用户优先分配系统的子载波和发射功率,最后再分配剩余的功率。文献[8]提出了一种基于分组子载波的资源分配算法,在满足用户比例公平的条件下,能够最大化系统的吞吐量。
本文研究了OFDM下行链路系统的子载波和对应功率分配问题。在满足用户最小速率和子载波约束的条件下,形成了最小化系统功率消耗为目标的混合优化问题。通过变量代换,将原始问题转化为只与子载波分配有关的整数优化问题,并在此基础上提出了一种功率最小化的双层迭代子载波分配算法。每次内部迭代求解两个用户的局部最优值,在一轮内部迭代完成后,应用外部迭代判断收敛停止条件,最后通过数值仿真验证了所提算法的有效性。
1 系统模型和问题形成
考虑一个OFDM的下行链路系统,基站位于小区中心,通过总带宽为B的L个子载波与K个用户进行通信,每个子载波的宽度为W=B/L。第n个子载波相对第k个用户的接收信噪比为:

其中hk,n表示基站在第n个子载波上到第k个用户的信道衰落系数,pk,n表示基站在第n个子载波的发射功率,n0表示对应的高斯白噪声功率。假设每个子载波上的噪声相对独立,对其他子载波无干扰。
因此,第n个子载波在第k个用户上对应的传输速率为:

用户的服务质量以用户的传输速率表示,满足第k个用户的服务质量就是要满足该用户的最小速率rk。满足用户k的服务质量需要的子载波个数αk,由用户的最小速率和其占用的子载波的传输速率决定。

令Gk,n=|hk,n|2/n0表示第n个子载波在第k个用户上的接收信道增益。假设同一用户使用的子载波具有相同的接收信道增益,即Gk,n=Gk。令基站分配给第k个用户的子载波数为lk。在保证用户服务质量的条件下,以使系统的总功率消耗最小为目标函数,形成问题如下:

其中,(a)表示优化目标为最小化系统的总功率消耗;(b)表示用户k的最小速率rk得到满足;(c)表示基站分配给用户的子载波总数;(d)表示基站的发射功率非负;(e)表示分配给第k个用户的子载波数目lk为正整数。由于需要优化的变量lk和pk分别为正整数和正实数,问题(4)是一个难以求解的混合优化问题。随着lk和pk的增加,用户速率也增加。令式4(b)取等号,可得到系统的最小消耗功率[6]。基站给第k个子载波的发射功率为:

问题(6)是一个整数优化问题,最优的子载波分配的必要条件为为了降低总的功率消耗,系统应该使用全部的子载波。对问题(6),穷举搜索算法通过枚举所有可能的子载波组合,从中挑选系统功率消耗最小的子载波组合作为最优值,因此穷举搜索算法的复杂度较高。
2 双层迭代子载波分配算法
在用户调度已知的条件下,受文献[9]的启发,利用问题特点提出了一种双层迭代子载波分配算法,可使系统的功率消耗最小。提出的算法由内部迭代和外部迭代组成。将每个用户从左向右排列,先随机给每个用户分配子载波。在每次内部迭代中,先固定相邻的两个用户的子载波个数,然后利用一维优化算法求解此时两个用户的子载波分配局部最优值。保留前一用户的子载波值为本次内部迭代的最优值,把后一用户与下一用户固定,继续执行相同的内部迭代。内部迭代算法每次向右选择一个用户,直到最后一个用户,因此需要进行K-1次内部迭代才能对所有用户进行子载波分配完毕。在K-1次内部迭代结束后执行外部迭代。外部迭代将本轮K-1次内部迭代后的总功率消耗和上次进行比较,判断如果满足条件,则终止迭代,否则继续进行内部迭代。可以看出,本文提出的算法既可用于整数优化问题,也可用于实数优化问题。
以基站将L个子载波分配给3个用户为例,说明提出的双层迭代子载波分配算法。从左到右把3个用户标记为用户1、用户2、用户3,初始化时随机给3个用户分配的子载波数分别为l10、l20和l30,有 l10+l20+l30=L。令 b10=l10、b20=l20、b30=l30进行第一次内部迭代,固定b10+b20,利用一维搜索算法求解用户1和用户2的功率消耗之和的最小值b11和b21,把b20赋值为b21,即b21=b20,有b11+b21=b10+b20。对第二次内部迭代,固定b20+b30,利用一维搜索算法求解用户2和用户3的功率消耗之和的最小值b21和b31,有b21+b31=b20+b30。经过两次内部迭代算法,完成一次对所有用户的子载波分配,即l11=b11、l21=b21和l31=b31。两次内部迭代后进行第一次外部迭代,外部迭代用来判断经过一轮内部迭代的子载波集合[l11,l21,l31]相比上次子载波集合[l10,l20,l30]的总功率的差值是否满足阈值ε。如果总功率差值小于阈值,迭代停止,[l11,l21,l31]为最优的子载波分配;否则,进行下一轮内部迭代和下一次外部迭代,直到满足收敛条件。
提出的双层迭代子载波分配算法如下。
参数初始化:总带宽B,子载波个数L,用户个数K,接收信道增益Gk,用户k的最小速率rk。
迭代初始化:随机初始化分配给用户的子载波[l10,l20,…,lK0],计算总的功率消耗P0,令[b10,b20,…,bK0]=[l10,l20,…,lK0]。
第t次外部迭代
for t=1:(L-K)
第m次内部迭代

收敛性判断
if Pt-Pt-1≤ε
Else
t=t+1;
继续下一次外部迭代。
end
3 仿真结果与数值分析
本文中的OFDM下行链路系统采用LTE标准中的信道衰落模型[10]:

其中dk表示用户k到基站的距离,此外对快衰落统计其平均值。子载波宽度设为1 kHz,白噪声功率为-115 dB。用户在小区内服从均匀分布,所有用户的最小速率设为1 kb/s。
图1、图2和图3分别仿真了在不同子载波初始化条件下,3个用户分配的子载波随迭代次数的变化关系,3个图的子载波初始化集合分别为(6,6,6)、(1,2,15)和(15,1,2)。迭代次数0代表子载波初始化,系统中的3个用户距离基站分别为300 m、400 m和500 m,表示为用户-300 m、用户-400 m和用户-500 m。图1表示平均初始化子载波,每个用户分配相同的子载波。图2表示初始化时,距离基站近的用户分配的子载波较少,距离基站远的用户分配的子载波较多。图3的子载波初始化情况和图2相反,每次内层迭代只对两个用户进行子载波分配,因此,只有两个用户的子载波分配情况发生变化。3种不同的子载波初始化情况下,经过不同的迭代次数,最终分配的子载波集合都为(3,6,9)。从3个图可以看出,子载波的初始化情况对提出算法的复杂度有影响。图1和图2的内部迭代次数都为6,而图3的内部迭代次数为8。
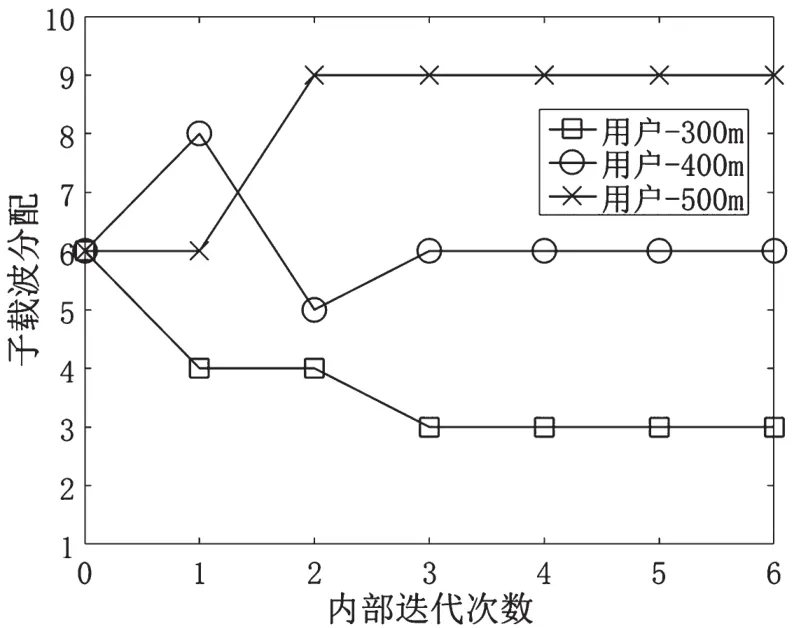
图1 子载波初始化集合为(6,6,6),子载波随内部迭代次数的分配
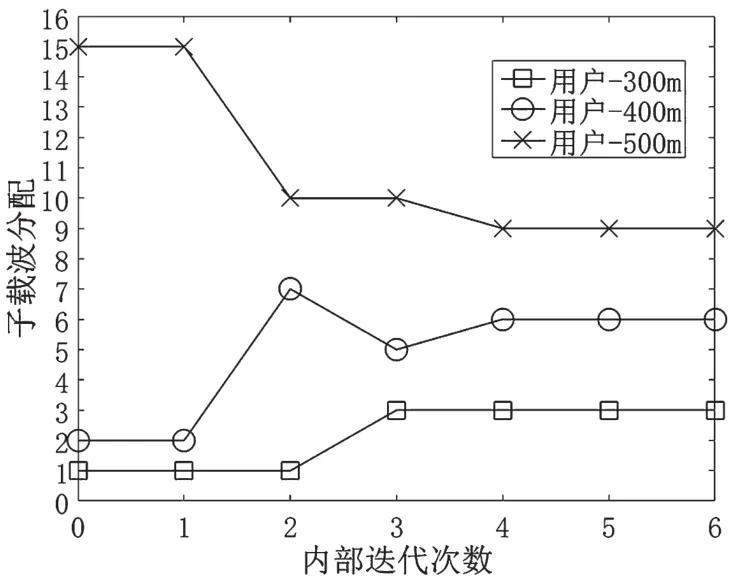
图2 子载波初始化集合为(1,2,15),子载波随内部迭代次数的分配
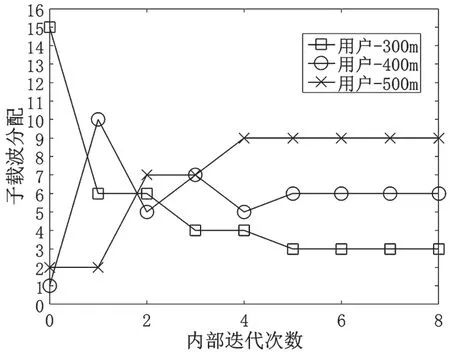
图3 子载波初始化集合为(15,1,2),子载波随内部迭代次数的分配
图4给出了不同的子载波初始化集合下,系统功率消耗随内部迭代次数的变化情况。3种条件下系统的功率随着内部迭代次数的增加而减小,分别经过3次、4次和5次内部迭代达到最优值,此时系统的最小消耗功率为43.6 W。

图4 不同子载波初始化集合下,总功率消耗与内部迭代次数的变化关系
4 结 语
本文研究了OFDM下行链路系统的子载波和对应功率分配问题,在保证用户最小速率的前提下,形成了关于子载波和对应功率分配的系统功率最小化的优化问题,即将原问题转化成一个关于子载波分配的整数优化问题,并提出了一种低复杂度的双层迭代子载波分配算法。最后,仿真结果验证了提出的算法的有效性。
