一种基于强度折减法的自适应安全系数算法研究①

2020-03-25伍礼杰邓红卫张亚南

矿冶工程 2020年1期

伍礼杰，邓红卫，张亚南

（中南大学资源与安全工程学院，湖南长沙410083）

稳定性分析是边坡工程建设、评估、治理中的重要内容，目前主要通过理论计算、试验研究和数值模拟等方法进行研究，其中利用强度折减法计算安全系数是目前最常用的数值模拟方法之一。保证安全系数计算准确的关键是精准判定边坡的状态，目前在边坡稳定性分析中常使用潜在破坏面贯通［1－2］、特征点位移突变［3］、能量突变［4－6］和数值计算不收敛［7］作为边坡失稳的判据，但前3 种判据对边坡临界状态的判定依赖在折减系数等增量变化下对判据变化的观察，且贯通塑性区发展部位的判断依赖于人的经验，在事先不能确定安全系数范围的情况下要想获得高精度的解，计算过程繁杂、效率低，即使采取增量细化搜索策略［8］进行优化，其计算量也非常庞大。数值计算不收敛判据的生效并不依赖折减系数等增量变化下某些观测量表现出的突变性和渐变贯通性，并能通过交叉二分法提高安全系数的搜索效率，使用方便且计算效率较高，因此在大型数值计算中具有良好的实用性。基于数值计算不收敛判据，许多研究通过各种方法来提高算法效率［9－12］，这在一定程度上对强度折减安全系数算法的搜索区间、搜索机制、初始应力状态回归等方面进行了优化，但对数值计算收敛判据的标准依旧采用人为划定的收敛限值和迭代计算上限，收敛限值过大会影响安全系数的准确性，过小则会提高计算收敛难度导致计算量过大甚至无法收敛；迭代计算上限过大或过小会导致边坡状态的误判，且过大的迭代计算上限还会导致计算量过大。寻找位于安全系数求解准确性和效率两者平衡点间的迭代计算上限值需要丰富的经验，所得结果会因人而异，故在保证安全系数计算准确性前提下提高求解效率的关键是采用合理数值计算不收敛判据。

本文从FLAC3D内置安全系数算法（以下简称内置算法）出发，针对内置算法的不收敛判据存在的一些不足，通过对安全系数搜索和计算流程中的系统失稳状态判定的优化研究，建立了一种原理简单、方便易用、准确高效的自适应安全系数算法（以下简称自适应算法）。

1 FLAC3D内置算法的机制与问题分析

1.1 内置算法原理

FLAC3D内置算法采用强度折减法计算边坡的安全系数，即不断折减材料的剪切强度以获取边坡临界平衡状态，此时的材料折减系数即边坡稳定性安全系数FS，其原理的表达式为：

式中c、φ 分别为材料的粘聚力和内摩擦角；Ftrial为折减系数；ctrial、φtrial分别为材料强度折减后的粘聚力和内摩擦角。

大多数工程边坡特别是失稳后亟需治理和处治后，要求边坡的安全系数介于0.5～2.0 之间，因此本文讨论的安全系数范围为［0.5，2.0］。FLAC3D5.0 软件的内置算法机制可以视为运用Ftrial搜索区间为［0.5，2.0］且首次Ftrial为1.0 的特殊二分法来逼近边坡临界状态的折减系数，其典型的求解流程如图1 所示，具体步骤如下：

1）初始计算条件设置，包括材料本构关系、性质和模型边界条件等参数的设置，重力加速度的施加等。

2）初始平衡计算，生成初始地应力，并对数值计算产生的变形位移、变形速度和塑性屈服区进行归零处置，获得模型初始应力状态文件。

3）系统特征响应时步Nr的计算，以摩尔-库仑本构模型为例，此计算过程的实质是给模型粘聚力和抗拉强度一个极大值，使系统内部应力状态产生巨大变化，默认给系统应力状态一扰动因子为2 的扰动，计算系统将历经多少时步回归平衡，这个时步值即为Nr，反映系统的求解计算难度。

图1 内置算法典型流程

4）采用交叉法猜测强度折减系数Ftrial的上下限值［v1，v2］，并用二分法不断试算逼近模型临界状态的FS。每经过Nr时步的强度折减迭代计算都会进行系统状态判定，当不平衡力比率小于收敛限值Rd（软件默认为1.0×10－5）时，则认为数值计算结果收敛，系统状态是稳定的，更新稳定状态文件FOSStable.f3sav。当某次迭代计算Nr时步后系统的平均力比率的变化量小于10%或者其变化量一直大于10%但迭代时步超过6Nr，都认为数值计算结果不收敛，系统处于失稳状态，更新失稳状态文件FOSUnstable.f3sav。以上条件都不符合时，系统处于未确认状态，进入下一轮Nr时步的迭代计算，直到满足条件后才会退出强度折减迭代计算。

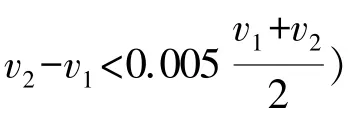
1.2 内置算法存在的问题分析

FLAC3D5.0 内置算法的本质是传统强度折减法，虽然有着众多优点，但在计算边坡安全系数时依旧存在有待改进之处，比如对粘聚力和内摩擦角的同比例折减策略并不完全符合实际边坡失稳破坏过程中粘聚力和内摩擦角的变化［13－14］，边坡失稳状态难以精准判定等。图2 为内置算法计算过程中不平衡力比率和折减参数的时变曲线，可以看出在时步（6.5～13）×104计算阶段的三次强度折减中，计算结果不再收敛，但算法并不能及时精准识别这一系统状态。结合内置算法的求解流程分析可知，以特征响应时步Nr作为分析单位过于保守，对系统失稳状态的识别度较低，在采用不平衡力比率判定系统状态时，无法及时有效识别系统失稳状态使得求解时间变长，效率变低，尤其对于尺寸大、网格密度高和工况复杂的大型数值模型计算，安全系数求解时间会随着求解难度的提高明显变长，而且限于软件权限，内置算法无法对边坡折减过程进行连续监测以及在大变形模式下计算安全系数。

图2 某例内置算法求解不平衡力比率及折减系数时变曲线

2 自适应算法的机制与实现

2.1 自适应算法的求解机制

根据上述分析可知FLAC3D内置算法求解效率较低是因为计算过程中对系统失稳状态的判定比较保守，不能充分利用强度折减迭代计算结果中蕴含的信息，常存在已经可以判断系统处于失稳状态但软件仍继续计算的情况。本文在进行这种数值计算时发现所有的失稳状态下的不平衡力比率时变曲线都符合前期迅速下降、后期平稳波动的规律，具体如图3 所示。可以看出Ⅰ区域曲线下降速度快、幅度明显，计算收敛迅速，Ⅱ区域曲线在某一稳定值上下波动，但变化幅值极小，一般而言整个计算周期不平衡力比率最小值会出现在这一区域，Ⅲ区域曲线以极缓极小幅度上升，表明数值计算不再收敛，系统失稳。

图3 某例求解不平衡力比率时变曲线

为解决内置算法计算效率低的问题，本文利用不平衡力比率变化量来表征强度折减计算过程中失稳状态下的不平衡比率时变曲线的变化规律，通过比特征响应时步更小的分析单位来观测折减计算的收敛情况，提出一种改进的安全系数求解算法——自适应算法，其主要机制如下：

以NS取100 时步为分析单位，提取n·NS时步后的不平衡力比率Rn，并与（n－1）·NS时步后的不平衡力比率Rn－1做差值，得到当前第n 次分析计算的不平衡力比率变化量Vn：

Vn反映出第n 次分析计算过程中不平衡力比率的收敛速度，分析Vn在不平衡力比率时变曲线不同阶段的特性，易知：

1）第n 次分析计算处于Ⅰ区域时，Vn＜0，且其值随着时步增加而增加，其绝对值随着时步增加而减小；

2）第n 次分析计算处于Ⅱ区域时，Vn值有正有负，其值在0 上下以极小幅值波动；

3）第n 次分析计算处于Ⅲ区域时，Vn＞0，Vn值稳定且极小。

从强度折减迭代计算开始到不平衡力比率最小值出现结束，Vn的绝对值逐渐减小且逼近0，而失稳状态的实质就是系统的不平衡力比率无法在实际可行的有限时步内达到收敛限值以下。因此为识别系统失稳状态，理论上可以通过Vn来预测系统当前达到收敛限值需要的最少计算时步Ni，人为设定Ni的限值（取1.0×105），当Ni超过限值时，认为系统不具备在实际可行的有限时步内达到稳定状态的可能性，即系统处于失稳状态。

定义一个新的变量目标收敛特征比Tn，用以表征当前循环不平衡力比率变化量占比目标差值Rn－Rd的多少，其计算如式（4）所示，相应的Tn的限值D1可由式（5）确定，当Tn＞D1时，说明系统处于失稳状态。

根据Vn的变化规律可知，当前观测到继续计算Ni时步后无法收敛，意味着实际这个预测的判断区间长度是不止1.0×105计算时步的。与内置算法的最大判断区间长度3.0×105计算时步（实际绝大多数情况下，这个判断区间是达不到的）相比，两者处于同一数量级，因此出于计算效率和实用性的考虑以1.0×105为判断区间是合理的。由于本算法的分析单位NS相较于内置算法很小，其更新频率高、能更快识别出系统失稳状态，故这种判断方法效率更高。所有采用数值计算收敛判据的强度折减安全系数算法结构都是折减参数循环包含着折减计算循环，自适应算法能提高每一个系统状态失稳的计算循环，从而明显提高安全系数求解效率。

2.2 自适应算法实现与计算流程

自适应算法采用NS作为折减计算循环单位，由于其计算时步较短，使得其失稳状态识别功能的适应性较弱，受限于网格数量、模型条件和工况条件等，可能会出现计算奇异点对这个识别功能带来干扰，计算结果会失准。为了避免出现上述情况，本文设计了多重判断机制来避免识别功能陷入计算奇异点的陷阱。执行的失稳状态判定条件有：

1）判定的前置条件：①某次计算循环的预测迭代次数超过Ni且其不平衡力比率变化量是负值，即D＜Tn＜0。②连续5 次计算循环的不平衡力比率变化量是正值，即min [ Tn－4，Tn－3，Tn－2，Tn－1，Tn]＞0。③以10NS时步为间隔，某次最大不平衡力比率Un不再减小，即Un－Un－9＞0。

当条件①、②或③累计出现次数超过1 次后，视为前置条件已满足。

2）单个分析单位的最终判定条件：当前置条件达到后，连续3 次小循环的预测迭代次数超过Ni，即min [ Tn－2，Tn－1，Tn]＞0，认为当前系统为失稳状态。

上述3 种最终判定条件只要满足其中一种就判定系统处于失稳状态，系统稳定状态的判定则与内置算法一样，以不平衡力比率小于收敛限值为条件，一旦失稳或稳定判定条件生效，算法就会退出当前的强度折减计算。其他情况则属于系统状态未确定，算法继续强度折减迭代计算，直至系统状态可以判定。

这种判定机制的建立是基于不平衡力比率时变曲线的变化规律，前置条件的判断是为了保证计算阶段已处于平稳波动区，条件2）则是通过多次识别系统的失稳状态，进一步精确判断系统状态，降低误识别的机率；条件3）和4）则是为了充分利用已经计算得到的不平衡力比率数据，在保证失稳状态识别功能完备前提下弹性调整判定限值，避免进入计算奇异点，陷入死循环。

自适应算法采用软件提供的FISH 语言编写实现，系统状态判定采用前述的判定机制，具体流程如图4 所示。

图4 自适应算法典型流程图

3 自适应算法的验证与分析

3.1 自适应算法的可靠性验证

为对比内置算法与自适应算法在求解结果上的差异和求解效率上的优劣，参考文献［15］中的模型数据和参数设置了4 个具有代表性的边坡模型来进行对比分析，其边坡具体尺寸如图5 所示，模型宽度统一取5.0 m，其材料参数如表1 所示，安全系数都处于［0.5，2.0］区间内。

图5 4 种边坡网格构形

表1 材料参数

建模时采用Midas GTS NX 进行网格划分，网格类型为四面体＋六面体的混合网格，网格尺寸为1.0 m，模型底部施加3 方向位移约束的边界条件，四周施加垂直面的方向位移约束的边界条件，上部施加自由边界。为保证计算效果的可靠性，两种算法对同一边坡进行安全系数计算时采用的网格模型、重力加速度、材料参数和软硬件环境保持相同，求解精度均取0.001。

表2 和表3 分别为自适应算法与内置算法求解的安全系数和所需的计算时步，可以看出两种算法求解结果差异非常小，4 个边坡自适应算法结果与内置算法结果的差值比分别为0.52‰，1.86‰，0.00‰和0.00‰，但在计算时步上自适应算法与内置算法相比，4个边坡的计算时步分别减少了42.24%，65.75%，39.90%和18.98%。这说明自适应算法不仅求解结果是准确的，而且在求解效率上是大于内置算法的，因此自适应算法一定程度上改进了内置算法存在的系统失稳状态识别效率低的缺点。

表2 安全系数对比

表3 计算时步对比

3.2 网格密度对自适应算法求解结果的影响分析

为进一步研究在大型数值计算中网格密度对两种算法的计算结果差异的影响，以边坡（c）为基础，划分0.3～1.2 m 共10 种不同网格尺寸的模型，获得了不同网格密度下两种算法所得的安全系数、求解时步和求解时间，具体结果如表4 和图6～8 所示。

由表4 和图6 可知，2 种算法求解的安全系数曲线的变化规律基本相同，数据差异很小，始终保持在1.1%以下，说明网格密度对自适应算法计算结果的准确性基本上没有影响。由表4 和图7 可知，随着网格密度增大，内置算法的求解时步总体上不断增大，而自适应算法所需的求解时步能够始终保持在一定的数值范围内，对比内置算法平均能够减少55.62%的求解时步，自适应算法在计算时步上的优化效果显著。由表4 和图8 看出，随着网格密度增加，2 种算法的求解时间都在增加，但自适应算法的增幅小于内置算法，相比内置算法，自适应算法平均能够减少50.10%的求解时间。因此自适应算法在计算效率上比内置算法具有更加明显的优势。