亚声速矩形射流的噪声辐射特性和声源分布

2020-03-25张俊龙雷红胜田昊李杰

航空学报 2020年2期

张俊龙，雷红胜，田昊，李杰，*

1. 西北工业大学航空学院，西安 710072 2. 中国空气动力研究与发展中心气动噪声控制重点实验室，绵阳 621000

射流噪声问题是气动噪声研究中的一类经典问题，普遍存在于航空发动机、火箭推进器、开口风洞以及各类排气系统中。随着民航业对噪声排放关注度的增加，射流噪声问题引起了越来越多的关注，研究人员采用数值模拟和试验手段对射流噪声机理、辐射特性及降噪措施等进行了较为系统的研究[1-3]。近年来，对非轴对称射流尤其是矩形射流的研究越来越引起重视，其广泛应用于新型隐身战斗机的二元喷口、超声速验证机尾喷口[4]、机翼增升的吹气流动控制喷口[5]等。尽管国际上进行了不少的矩形射流噪声的试验和计算研究[6-10]，但是不同研究结果对矩形射流噪声辐射特性的认识还存在一些差异，如文献[7]指出，相同喷口面积的矩形射流和圆形射流频谱差异较小；而文献[11]表明，特定宽高比(Aspect Ratios，AR)的矩形射流噪声较圆形射流明显偏小。文献[6]指出，矩形射流噪声辐射存在明显的周向不对称性，不同周向位置的辐射频谱存在一定的差异。在射流噪声降噪研究中，通过调整非轴对称射流噪声辐射的周向分布，来降低特定方向的噪声辐射，将会是一个潜在的降噪手段。

对射流噪声进行定位研究有助于研究人员对射流噪声机理的进一步认识[12]，有助于更细致地对射流噪声辐射特性进行评估[13]。射流噪声的噪声源定位研究还可用于揭示不同类型射流湍流混合剪切层的增长率。Nick和Ahuja[14]的研究表明，射流噪声声源越靠近上游，表明湍流混合剪切层增长越快，向远场辐射的总噪声级越小。早在20世纪70年代，Laufer等[15]就采用了声聚镜的方法对射流噪声进行了定位测量研究。Fisher等[16]建立了极角相关法，将射流噪声看成轴向分布的线声源，通过不同极角位置处的传声器和参考传声器之间声信号的相关关系得到不同频率下射流噪声沿着轴向的分布情况。20世纪90年代以来，基于波束成形(Beamforming)算法的传声器阵列噪声源定位技术逐渐成熟[17]，并被用于射流噪声的定位测量中[18-21]，成为了主流的射流噪声定位工具。目前的噪声源定位研究主要围绕轴对称射流进行。James等[22]采用了数值虚拟的传声器阵列针对宽高比为4∶1的矩形喷口和矩形斜掠喷口进行了噪声源定位的数值模拟研究。真正的矩形射流噪声源定位的试验研究目前还开展得较少。

本文基于射流噪声模拟试验台，采用更换喷口的方式，对相同出口面积，宽高比分别为1、1.5、2、10的矩形亚声速射流进行了较为系统的射流噪声远场辐射特性研究。通过远场噪声测量，获得了不同宽高比矩形喷口在不同方位角平面的射流噪声频谱分布结果相对于圆形喷口射流噪声的差异。通过基于波束成形算法的传声器阵列，获得了矩形射流噪声源峰值位置随频率的变化情况，系统分析了射流速度、方位角、宽高比等参数对矩形射流定位结果的影响。本文研究成果对于进一步揭示亚声速矩形射流噪声产生机理和研究新的射流降噪措施具有较强指导意义。

1 试验装置和方法介绍

1.1 试验装置和设备

1.1.1 射流模拟装置

本项目射流模拟装置如图1所示。该装置建立在全消声室内。消声室净空间尺寸为10.8 m×8.4 m×7.0 m(长×宽×高)，截止频率为100 Hz。消声室满足ISO-3745标准，本底噪声仅为7 dB(A)。射流模拟装置的动力来源于压力为2 MPa、容量为20 000 m3的中压气源，通过两级调压控制系统实现对目标压力的精确控制，控制精度达0.1%。整个装置最大供气质量流量为2 kg/s，核心区射流马赫数最大可达1.8。

图1 射流模拟装置照片

1.1.2 传声器及传声器阵列

本试验远场测量传声器和阵列传声器均采用1/4英寸G.R.A.S.46BE自由场传声器，前置放大器为G.R.A.S.26CB。其频率测量范围为4 Hz～80 kHz；动态范围为35 dB(A)～160 dB；灵敏度为4 mV/Pa。

数据采集系统为基于NI板卡的128通道动态数据采集系统。该系统的最高采样频率为204.8 kHz；模数转换位数为24 bit；精确度≤±0.1 dB；动态测量范围>120 dB；抗叠混保护>110 dB。

传声器阵列为70通道的多臂螺旋结构阵列。阵列内传声器最大间距为1 m，传声器的具体布置阵型如图2所示。

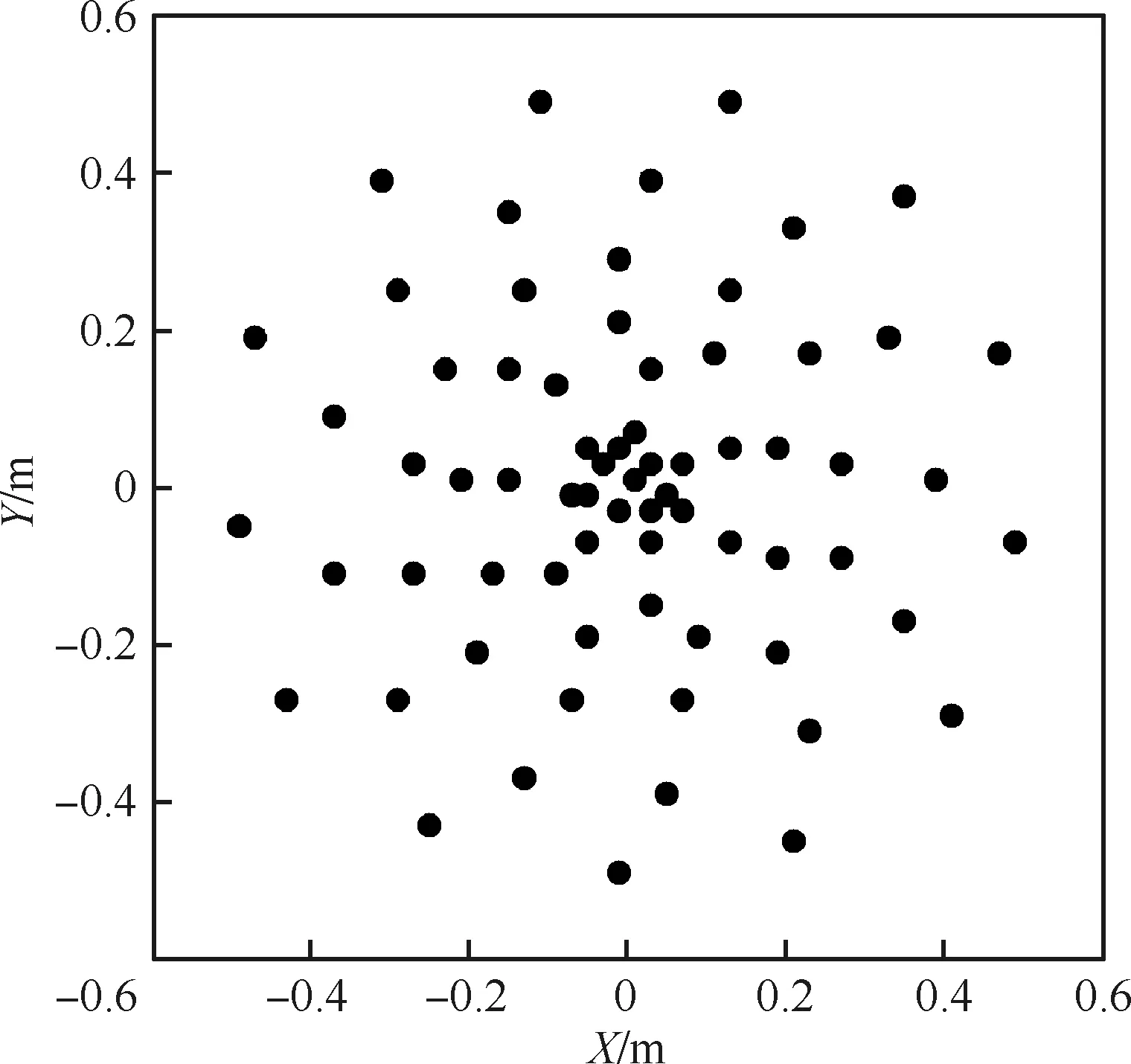
图2 70通道传声器阵列布置方案

1.2 试验方案

本试验所使用的喷口包括圆形喷口和宽高比分别为1、1.5、2、10的矩形喷口，所有喷口的出口截面积均为25 cm2，唇口厚度为8 mm。文献[23]表明，来流条件及边界层分布对射流噪声定位和传播特性有较大影响。本试验不同外形的喷口通过更换收缩段和喷口的方式实现切换，这样就保证了上游管路和控制参数的一致性。同时，本试验所有喷口的上游收缩曲线均采用相似的多段样条平滑曲线统一加工，使得不同截面形状的射流来流条件和边界层分布均具有很好的一致性。以上措施确保了试验得到的圆形射流和矩形射流的噪声辐射特性及噪声源分布的对比结果精确、可信，具有指导意义。

本文针对矩形射流的轴系定义如图3所示。其中XOZ平面为长轴平面，XOY平面为短轴平面，介于XOY和XOZ平面之间、周向角(Φ)为45°的平面定义为斜角平面。试验在XOY平面、XOZ平面及斜角平面之间的切换采用转动喷口上游收缩段入口处法兰的形式进行，该形式确保了试验过程中远场传声器或阵列传声器与喷口的相对位置保持不变。

图3 矩形射流坐标轴定义

远场测量时，传声器的布置方式如图4所示。图中所示为与射流轴线同高的水平面。在该平面上，以射流喷口出口中心为原点，在半径r= 3 m(约53D，D为喷口直径)的圆上布置测点，测点极角(θ)覆盖的范围为30°～120°。

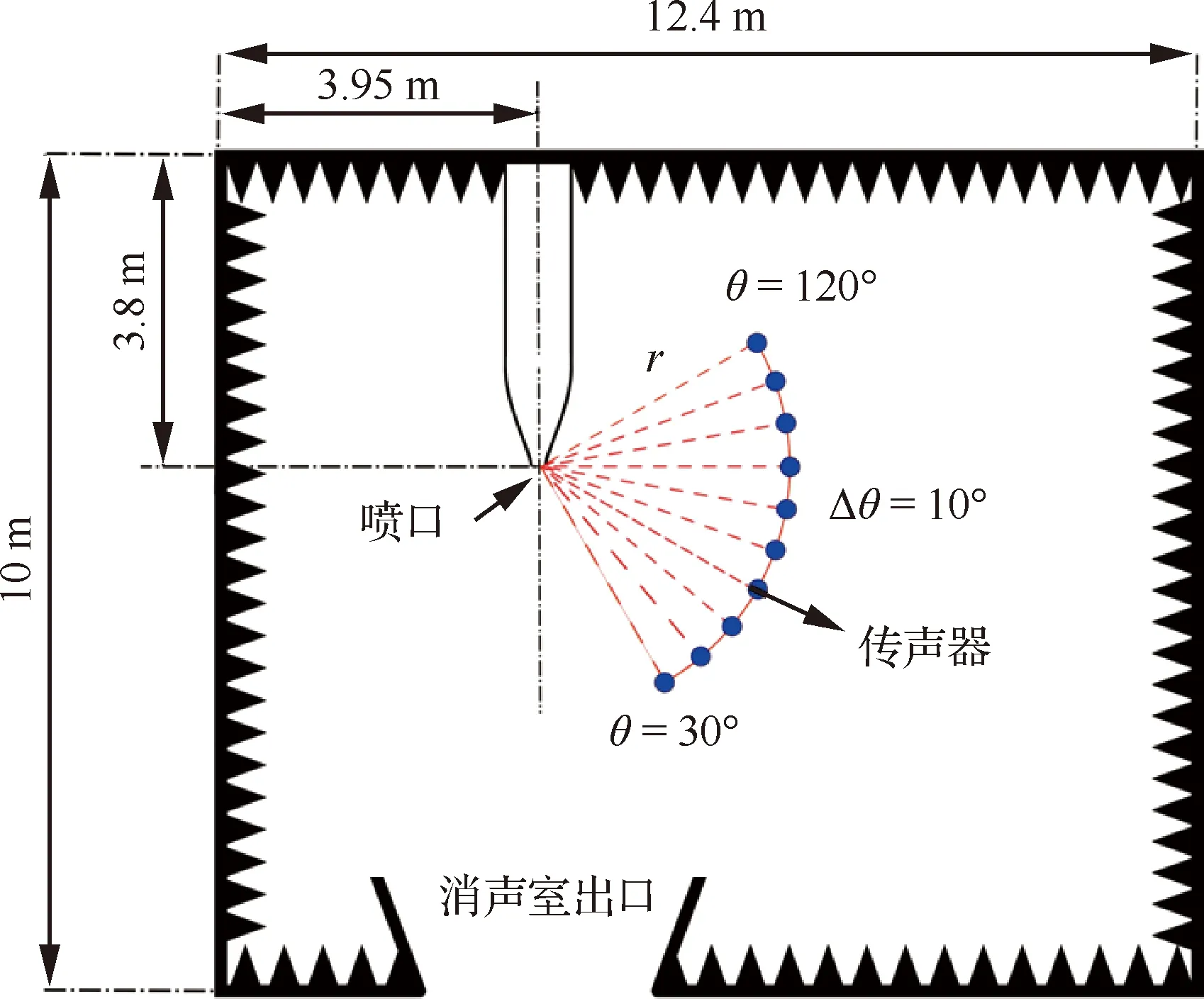
图4 射流远场噪声测点布置示意图

传声器阵列测量如图1所示。传声器阵列位于喷口侧面，阵列平面与喷口轴线平行，阵列中心正对喷口出口截面中心，距离喷口出口中心2.15 m。

试验时，为减小测量装置之间的干扰，远场噪声测量与阵列定位测量分别单独进行。试验时，所有传声器同步采集，采样频率为204.8 kHz，采样时间设为20 s。

1.3 数据处理方法

1) 远场噪声数据处理方法

远场噪声数据的频谱分析采用Welch求功率谱密度(Power Spectrum Density,PSD)的方法进行，将数据分为多块，每块加窗函数进行傅里叶变换，然后进行平均，每个数据块数据个数为8 192，窗函数采用Hanning窗，所分析的窄带信号的频率间隔为25 Hz。传声器采用去保护罩的形式进行测量[23]，并进行了传声器频响特性修正、空气吸声效应修正[24]。

2) 传声器阵列声源识别方法

首先求出阵列传声器信号互谱矩阵。对于由M个传声器组成的传声器阵列，可形成一个M×M的互谱矩阵，互谱矩阵中每一个矩阵元素可通过快速傅里叶(FFT)变换取得。将每一个通道的数据分块，对每一块进行傅里叶变换得到频域的噪声信号，每块样本数为32 768个(窄带分析频率为6.25 Hz)。互谱矩阵计算表达式为

(1)

式中：

(2)

式中：K为传声器阵列数据分块数；Pm′k(f)为第m′个传声器第k段数据块的频域信号，f为目标频率；W为频谱分析所选取的数据窗函数常数，窗函数采用Hanning窗；上标“*”表示共轭。互谱矩阵下三角矩阵通过上三角对应矩阵元素的复共轭得到。

然后获得扫描点到阵列传声器的指向性向量。采用传声器阵列对潜在目标声源平面进行扫描，对于扫描平面上的任一扫描点，阵列的指向向量可表示为

(3)

式中：第m个传声器的指向因子为

(4)

式中：Am为第m个传声器的剪切层振幅修正因子；Rm为声波扫描点与传声器之间的传播距离，Rm=τmc0，τm为延迟时间，c0为声速；Rc为阵列中心点到扫描点之间的距离。

最后得到目标扫描平面的声源强度分布。目标扫描平面的声源强度分布即阵列在每一个扫描点的输出功率谱，其表达式为

(5)

(6)

式(6)为阵列扫描平面上某点位置处的输出功率谱。测量时，将目标扫描平面离散化为扫描点阵，利用式(6)求出每个扫描点的输出功率谱，所有点结果组合起来就可得到扫描平面的噪声源分布云图。

本试验噪声源定位分析结果采用1/12倍频程信号，在每个目标频段内对窄带信号能量求和而得到该频段的噪声源功率谱分布结果。

2 矩形射流远场噪声辐射特性试验结果

图5～图7分别给出了射流马赫数Maj=0.9时，矩形射流短轴平面、斜角平面以及长轴平面噪声辐射功率谱密度与圆形射流的差量(ΔPSD)云图。图中正值表示矩形射流噪声辐射能量大于圆形射流，St为斯特劳哈尔数，表征无量纲频率，其定义为

(7)

式中：U为射流核心区速度。

由图5～图7可知，宽高比为1的矩形射流与圆形射流远场噪声辐射特性差异较小，在各方位角平面以及各频率下，二者的噪声功率谱密度差量不超过0.7 dB。随着矩形喷口宽高比的增加，矩形射流远场噪声辐射特性与圆形射流的差异逐渐明显。总的来说，矩形射流高频段部分的辐射声能要大于圆形射流，低频段部分的辐射声能要小于圆形射流，且这个差异随着矩形宽高比的增加而明显增加。值得注意的是矩形射流短轴平面下游方向的噪声辐射结果。几乎在所有频段，矩形射流该位置处的噪声辐射功率，都要明显小于圆形射流。矩形射流的这种辐射特性值得在以后射流噪声降噪措施的研究中给予重视。

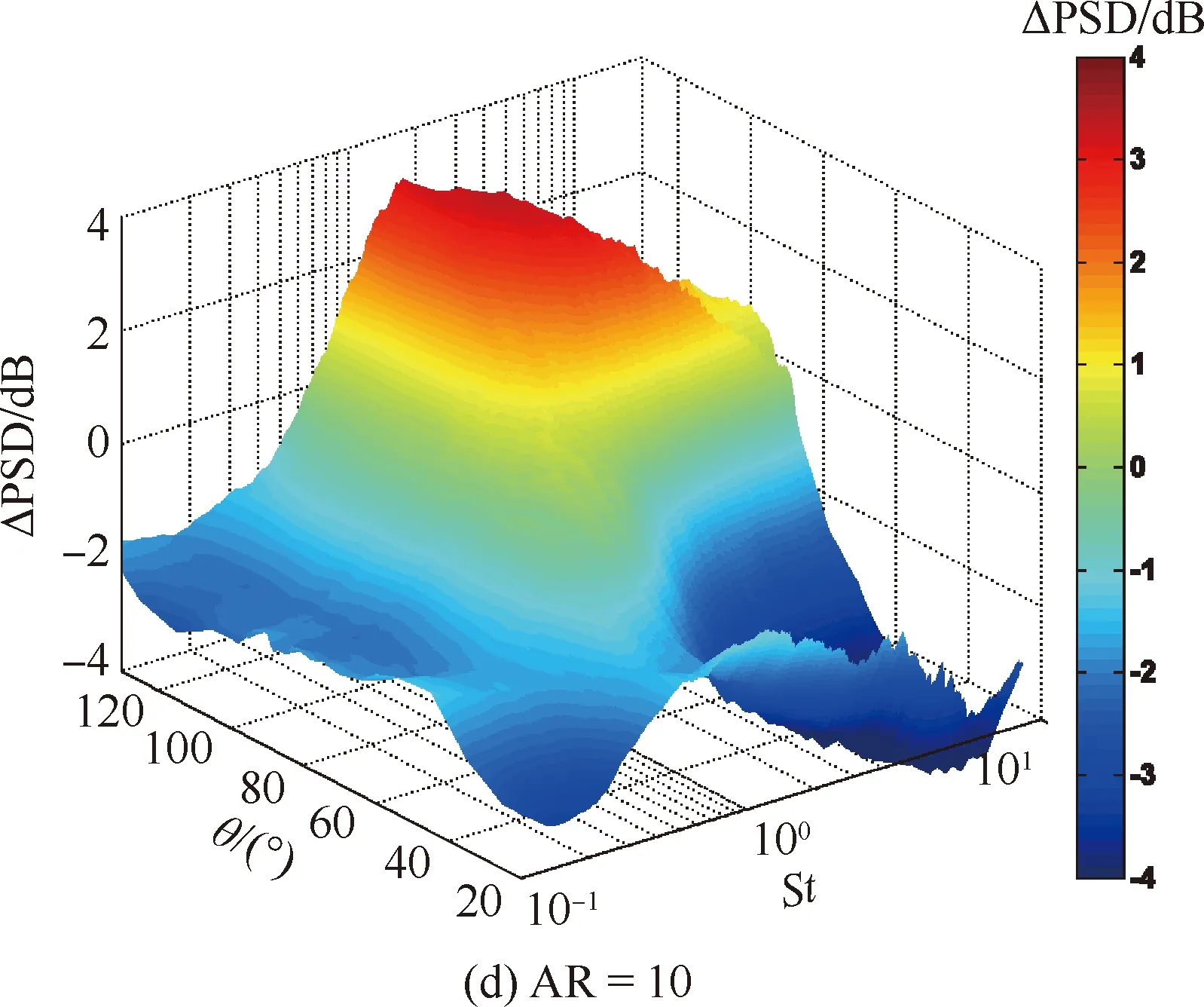
图5 短轴平面矩形射流噪声功率谱密度与圆形射流的差量

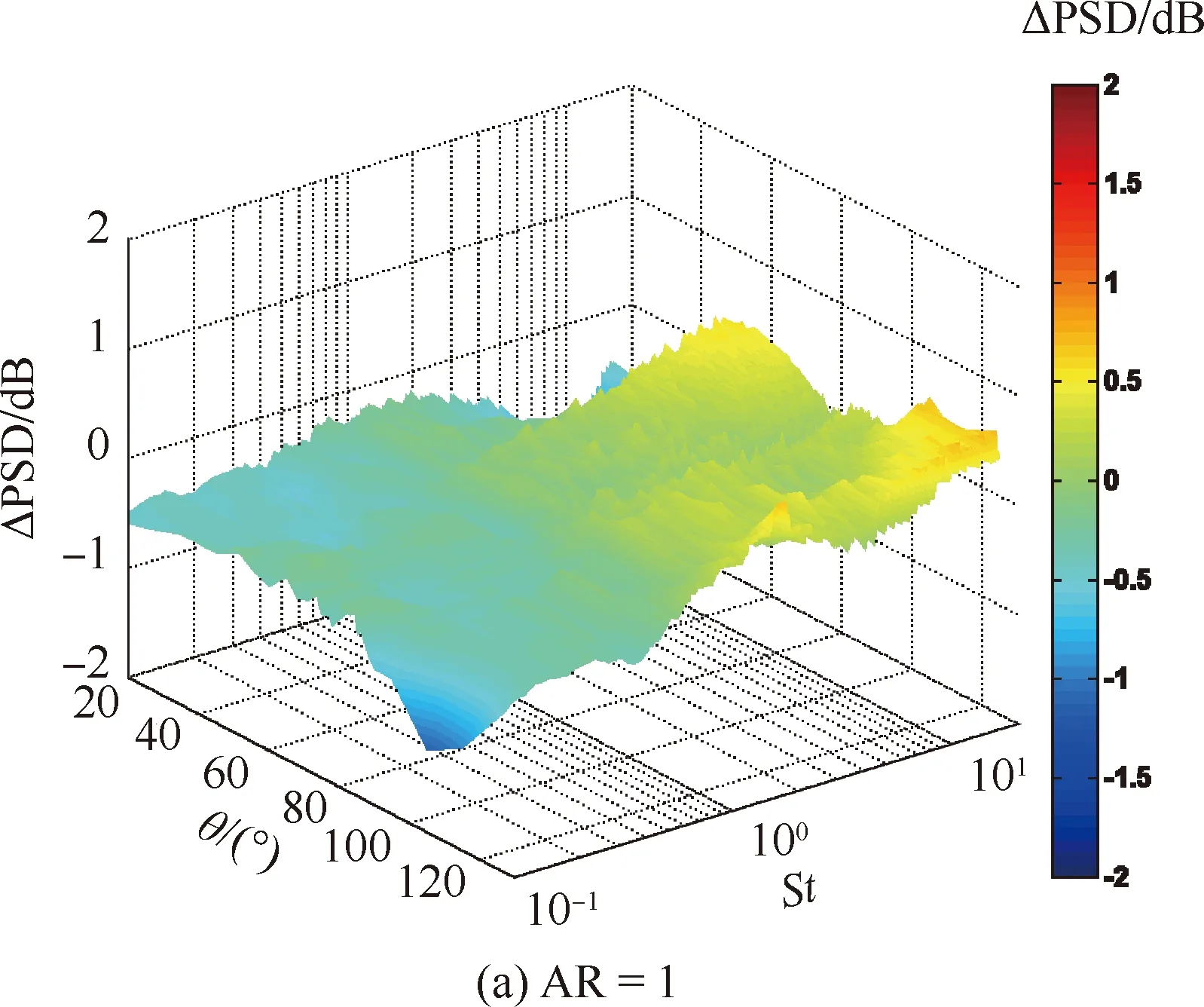
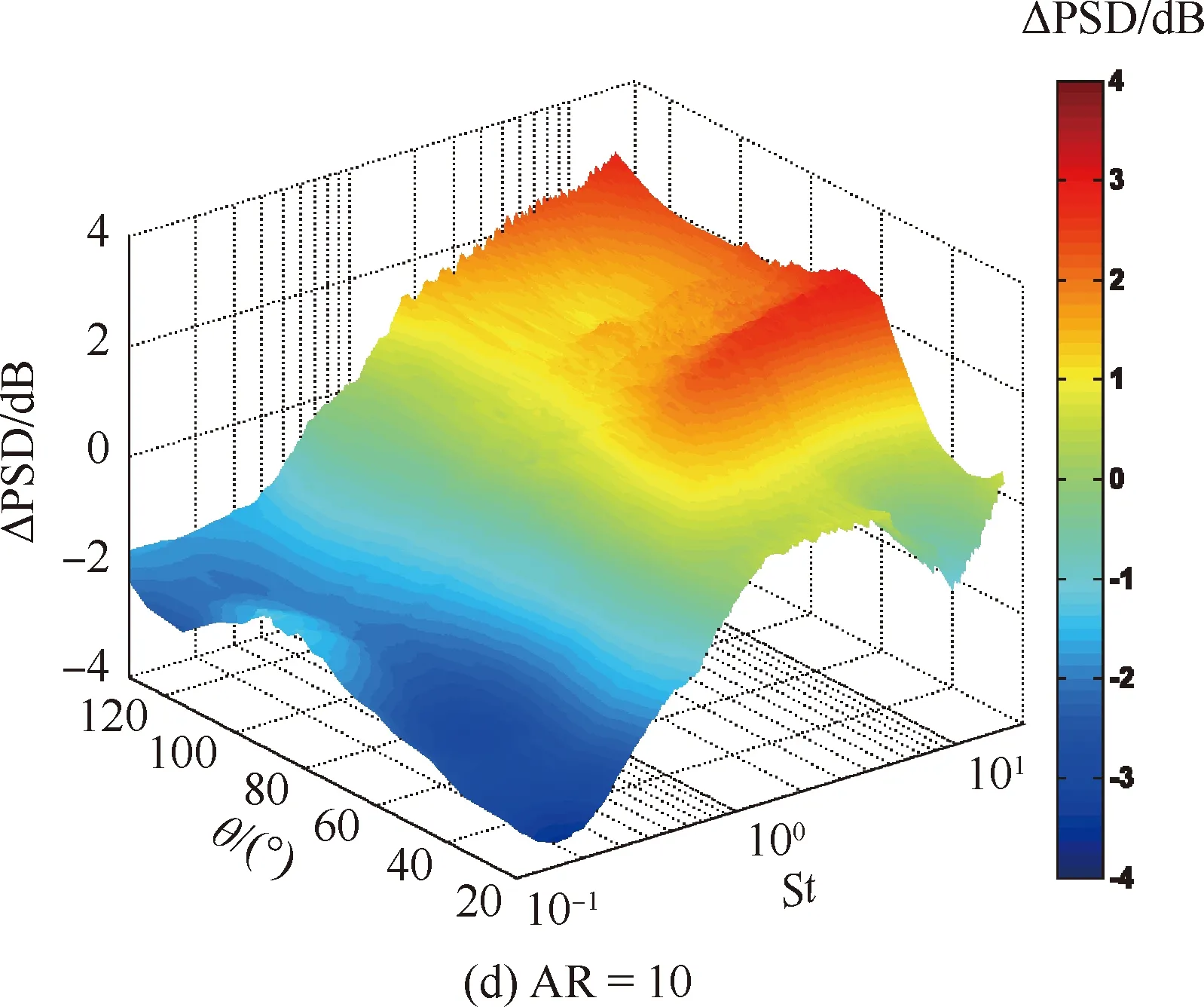
图6 斜角平面矩形射流噪声功率谱密度与圆形射流的差量

图7 长轴平面矩形射流噪声功率谱密度与圆形射流的差量

3 亚声速矩形射流噪声源定位结果

3.1 圆形射流噪声源定位结果

传声器阵列的分析频率下限由阵列尺寸决定，分析频率上限由传声器的最小间隔、定位误差等决定[25]。在低频段，频率越低，阵列的空间分辨率越低；而在高频段，频率越高，阵列云图动态范围越低，即旁瓣值越接近主瓣。最终阵列的频率分析范围需根据云图结果进行评估。

图8给出了Maj=0.7，目标频率分别为400、4 000、40 000 Hz时圆形单射流的声源定位云图，图中SPL表示声功率级。该云图由扫描平面上300(X向)×100(Y向)个点的结果插值而成。目标频率为4 000 Hz和40 000 Hz时，扫描点间隔为0.004 m；目标频率400 Hz时，扫描点间隔为0.012 m。

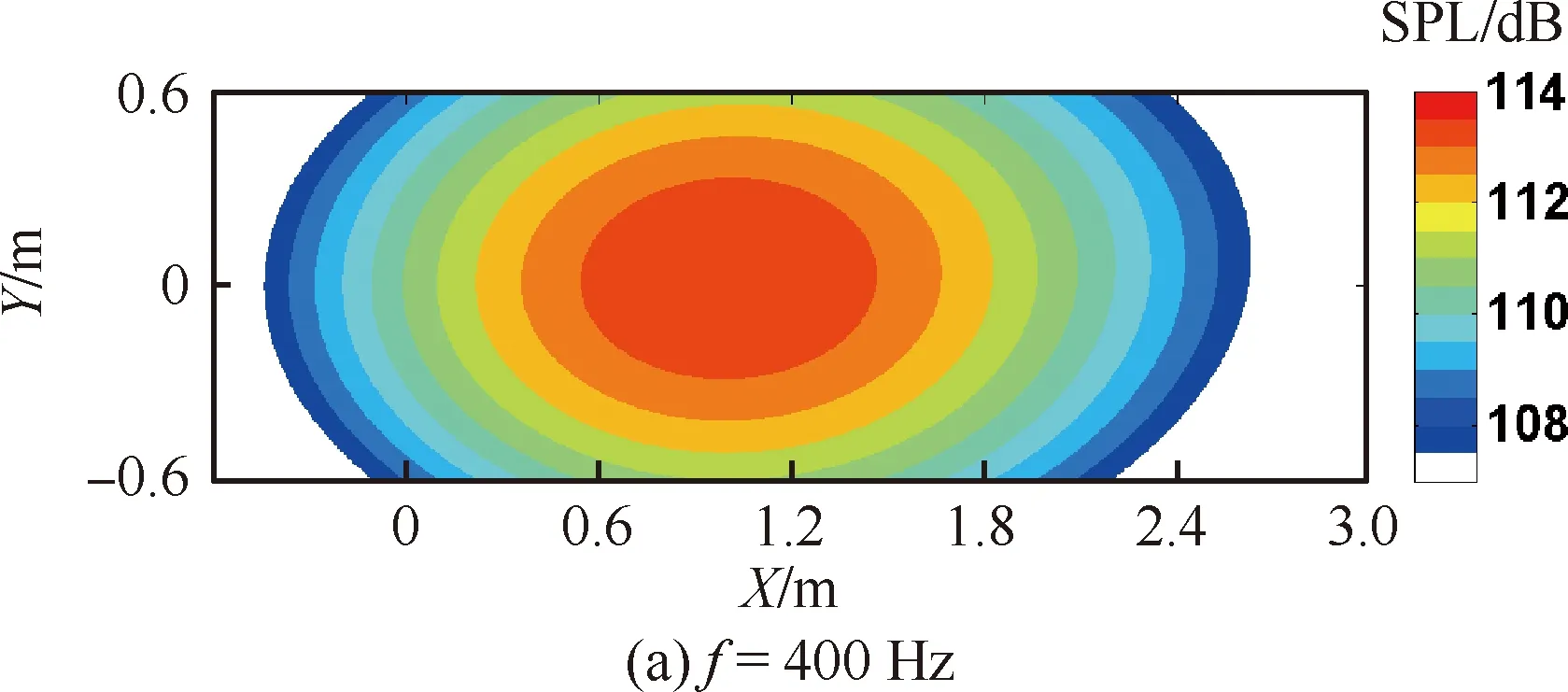
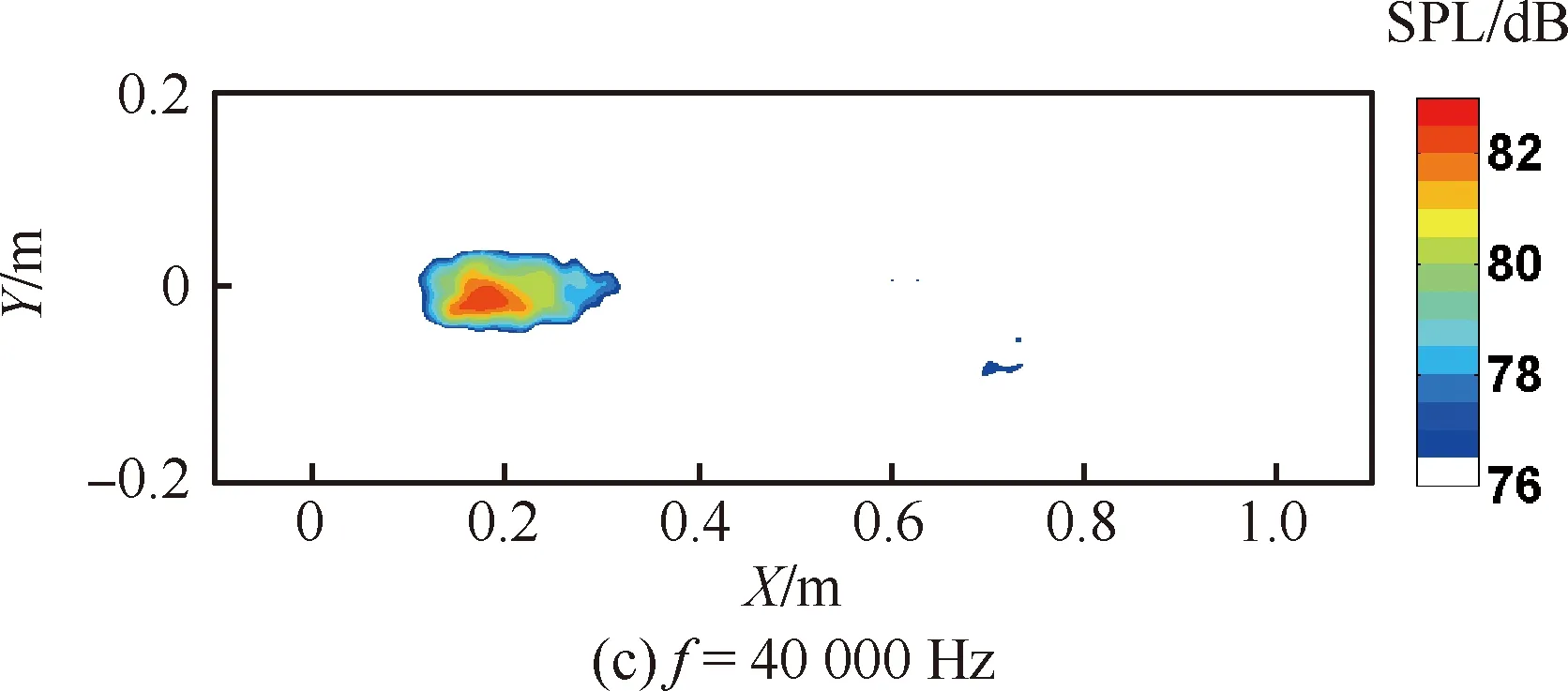
图8 圆形单射流噪声源分布云图

由图8可知，在频率400～40 000 Hz的范围内，本次试验所用的传声器阵列及其算法针对射流噪声都能够得到效果较好的云图。该试验条件下，400～40 000 Hz对应的无量纲频率St的范围约为0.1～10.0。

图9 试验获得的圆形单射流噪声源分布与文献[13,19-20]结果的对比

图9给出了试验获得的圆形单射流噪声源的分布结果与类似工况下文献[13,19-20]结果的对比。图中纵坐标为沿射流轴向(X向)的噪声源峰值位置(以喷口直径D进行无量纲化)，横坐标为无量纲频率St。图中的点表示该无量纲频率下噪声源定位峰值的轴向相对位置。由图可知，亚声速射流噪声源峰值位置随频率的升高而向上游方向移动，即低频射流噪声主要位于射流核心区末端，高频射流噪声主要集中在接近喷口出口截面的射流剪切层处。由图可知，本试验获得的射流噪声源的定位结果与文献中的结果具有很好的一致性。

文献[10]认为不同频率噪声源峰值位置与无量纲频率的指数近似呈线性关系。本研究相对文献结果进一步加密了频率分析间隔以及扩宽了频率分析范围。所得结果表明，在较宽频率范围内，不同频率噪声源峰值位置与无量纲频率的对数近似呈指数关系，而线性关系的拟合仅在中频段(St= 0.2～0.8)附近较为准确。以圆形射流射流马赫数Maj= 0.9时噪声源的分布结果为例，拟合结果如图10所示。由结果可知，频率范围向高频和低频段扩展后，不同频率噪声源峰值位置与无量纲频率的对数之间的关系用指数进行拟合的结果与试验更为相符，而用线性拟合则只与中频段范围结果相符，而在高频和低频段附近，其预测结果与试验结果相比存在较大偏差。

图10 圆形单射流噪声源分布的拟合结果

3.2 矩形射流噪声源定位结果

1) 不同方位角平面的噪声源定位结果对比

图11给出了射流马赫数Maj=0.9的条件下，宽高比分别为1.5、2、10的矩形射流在不同方位角平面的噪声源分布结果。由结果可知，矩形射流不同方位角平面的噪声源分布差异很小，只有宽高比很大时高频部分结果略有差异。此时，射流噪声定位云图如图12所示。由图可知，此时声源分布范围较大，呈扁平状布置。长轴平面定位结果噪声源主要位置在矩形射流窄边剪切层处，而短轴平面定位扫描平面是矩形射流长边的中心所在的平面，二者位置的不一致引起了不同周向平面测得的噪声源分布结果出现差异。

图11 矩形射流在不同方位角平面的噪声源分布(Maj=0.9)

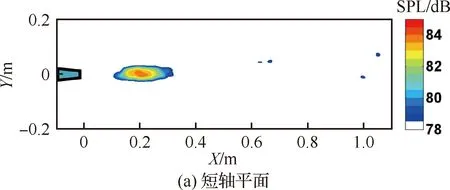
图12 矩形射流短轴平面和长轴平面噪声源分布云图(AR=10，St=8)

2) 射流速度对矩形射流定位结果的影响

图13给出了不同射流速度下宽高比分别为2、10的矩形射流长轴平面的噪声源分布结果。由于矩形射流长轴平面与短轴平面噪声源分布结果具有较高一致性，图13仅给出了长轴平面的典型结果。由结果可知，当射流马赫数小于1时，不同射流速度条件下，无量纲化的射流噪声源分布结果具有很好的一致性。当射流马赫数达到1时，射流内可能出现激波啸叫声及宽频噪声，此时射流的流场结构和声源特性与亚声速射流具有较大差异，导致二者定位结果出现较大的差异。

3) 宽高比对矩形射流噪声源定位结果的影响

图14给出了射流马赫数Maj=0.6时，不同宽高比的矩形射流噪声源分布结果与圆形射流的对比。由结果可知，矩形射流的宽高比对射流噪声源定位结果有较大影响。与圆形射流相比，在矩形射流低频段(St<1.5)，随着宽高比的增加，射流噪声源峰值位置向上游移动；在高频段(St>3)，随着宽高比的增加，射流噪声源峰值位置向下游移动。在1.5