叶片加工误差对压气机性能的影响

程超，吴宝海,*，郑海，高丽敏

1. 西北工业大学 机电学院，西安 710072 2. 西北工业大学 动力与能源学院，西安 710072

压气机是航空发动机的核心部件，其性能对航空发动机有着至关重要的影响。叶片是构成压气机的基本单元，相邻叶片构成的通道内流动情况决定了压气机的性能，现代多采用几何构型复杂的三维叶片来提升压气机性能，这类叶片型面复杂且属于薄壁件，在多轴数控加工过程中会产生加工变形[1]，使得叶片实际型线偏离原始设计，影响压气机的气动性能。

一般而言，叶片的加工误差会增加压气机的性能变异性，影响压气机的平均性能，为量化叶片的加工误差对压气机气动性能的影响，国内外学术界、工业界开展了一些研究，NASA LEWIS中心的Roelke等[2-4]试验研究了叶型轮廓误差、型面厚度变化、粗糙度、弦长误差对压气机气动性能的影响，并分析了误差位置对气动性能的敏感性。Goodhand和Miller[5-6]通过数值及试验研究了由于加工导致的压缩机静叶前缘几何、粗糙度、圆角等微小结构变化对气流分离和性能的影响。Daria等[7]通过数值计算研究了不同类型的透平叶片表面极限加工误差，如叶片弦长、叶型弯角、叶片高度等对于气动性能的影响，获取了极限加工误差下的参数对叶型性能的影响规律。文献[8-10]基于蒙特卡洛采样方法，对大量具有加工误差的叶片样本进行数值分析以找出叶片加工误差对气动性能的影响，结果较准确，但计算时间长、研究成本较高。Goodhand等[11]开展了压缩机叶片前缘加工误差与气动冲角范围的敏感性研究，结果表明经过鲁棒优化得到的不对称前缘能增加5%稳定运行冲角范围。高丽敏等[12-13]通过数值及试验研究手段分析了不同类型的叶片表面加工误差对于平面叶栅气动性能的影响。张伟昊等[14]采用非定常数值方法研究了3种涡轮安装角偏差对性能的影响，郑似玉[15]等研究了压气机叶片位置度、轮廓度及扭转度偏差影响性能的敏感性，颜勇等[16]基于非平稳高斯过程的加工误差模型，研究了加工误差对低压涡轮叶栅气动性能的影响，罗佳奇等[17]基于伴随方法研究了二维涡轮叶片加工偏差对性能的影响。上述研究大多为针对平面叶栅或三维叶片的若干个结构参数由于加工、安装误差而开展的单因素流动分析，对于三维复杂转子叶片受加工误差影响，多个结构参数同时改变后作用于压气机的性能研究很少涉及，因此所得结论不能完全用于指导实际压气机三维复杂转子叶片在多因素加工偏差影响下的设计加工。

三维复杂转子叶片的加工误差对叶型的前缘角、后缘角、前后缘形状、弦长、厚度均产生影响，同时不同叶高位置的加工偏差也不一致，这些典型结构参数的综合作用与单个参数影响压气机性能的效果不同，Fathi和Alizadeh[18]对涡轮叶片的6种单变量，即扭转角、叶片偏移、前缘和后缘厚度、两类倾斜和三维弓形变化影响涡轮单级的性能进行了分析，同时考察了单变量的一些简单组合对涡轮单级的性能影响，结果显示单变量的简单组合可使级质量流量和效率变化14.62%和1.8%，大大超过各单变量对级性能的影响，该研究指出了典型结构参数综合作用的重要影响，但是由于样本数少，没有考虑到整个偏差范围内研究样本的完整性，所得的结论并不全面。

由于三维叶片的端壁影响、顶部泄露，以及沿叶展的流动掺混使流动变得复杂，会对某些参数加工偏差影响二维叶型性能的机理产生抑制或增强作用，同时三维叶片多个参数加工偏差的综合作用会超过各单独参数加工偏差对级性能的影响，因此本文针对压气机三维复杂动叶片加工过程中的前缘角、后缘角、弦长、厚度、前后缘形状的偏离，以及不同叶高处的截面位置这6个典型结构参数综合开展加工误差研究，采用正交实验法在整个偏差范围内全面完整的研究这些参数的加工误差对压气机性能的综合影响，所得结论能够为进一步提升压气机三维叶片设计和加工的匹配性提供相关指导。

1 研究对象

尽管压气机叶片三维结构复杂，但其本质上是由多个叶型截面按照一定的规律积叠而成，叶型截面中主要几何参数如图1所示，叶型前缘角X1、后缘角X2、弦长b、厚度c(其中最大厚度cmax)，误差采用Δ表示，叶型前后缘形状常用的有3种，分别为圆形、椭圆形、钝边(目前前后缘的加工大部分需要手工抛光，根据设计需要，叶型前缘和后缘形状可以不一致，此处为简化设计和分析，将前缘、后缘两个形状变量简化为一个形状变量，假设每次加工的叶型前后缘形状保持一致)，三维结构的展向截面位置分别取叶顶(100%叶高)、叶中(50%叶高)、叶根(0%叶高)3个典型位置。

对某跨声速压气机叶片型线进行了三坐标精密测量，每个叶片有11个截面，共计47个叶片517个截面，与设计叶片相比，统计的517个截面中叶型前缘角偏差ΔX1=±1°，后缘角偏差ΔX2=±1°，弦长偏差Δb=±2%，厚度偏差Δc=±5%。

图1 叶型主要几何参数

由于叶型前缘角偏差、后缘角偏差、前后缘形状、弦长偏差、厚度偏差以及不同叶高处的截面位置这6个主要结构参数之间不相关，按照上述每个结构参数统计得到的误差范围给出3个水平，其中水平2中的数值0表示设计值，水平1、水平3中的数值分别表示极限偏差，6个结构参数的各水平见表1所示，上述6个结构参数对压气机性能的综合影响如果进行析因实验设计(即各种参数、水平的组合实验都要做)，共计需要36=729次实验，实验次数太多，为减少实验次数、降低实验误差，又要保证样本的全面性，最终采用正交实验法设计了27个正交实验样本，各实验样本参数详见表2。

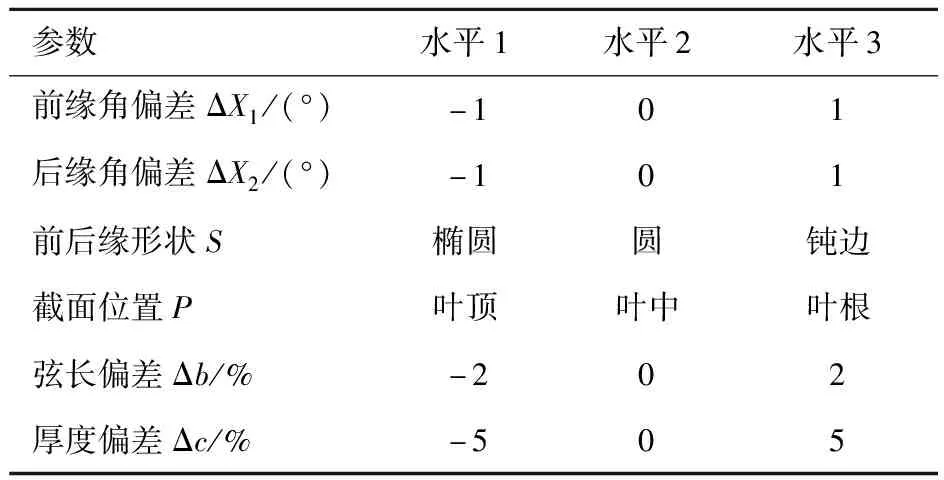
表1 几何参数的水平分布

表2 正交实验设计表

2 数值计算

使用商用软件Numeca对该跨声速压气机动叶片加工偏差开展流场计算分析，首先对原型压气机性能进行数值计算，验证数值计算的准确性，然后对产生上述加工偏差的27个正交实验样本进行数值计算，以量化其气动性能与加工偏差的关系。

2.1 数值方法验证

采用目前国内最高加工精度的方法加工出与设计叶型最大偏差±0.05 mm的压气机三维转子叶片，进行性能实验，同时对该转子叶片性能进行数值模拟，计算域进口从叶片进口位置延伸至3倍弦长处，出口从叶片出口位置延伸至2倍弦长处，计算域如图2所示。

图2 计算域示意图

数值计算采用Spalart-Allmaras湍流模型，采用单通道数值模拟，网格数量为81万，近壁面y+小于1。图3为该跨声速压气机在50%叶高截面的Ma分布，从图3可看出在吸力面的前半部分出现激波。图4为数值计算与实验结果的对比，从图4可以看出两者的趋势一致，总压比、效率和流量的整体偏差小于2%，表明数值计算结果能较好地预测实际性能。

图3 50%叶展位置马赫数分布

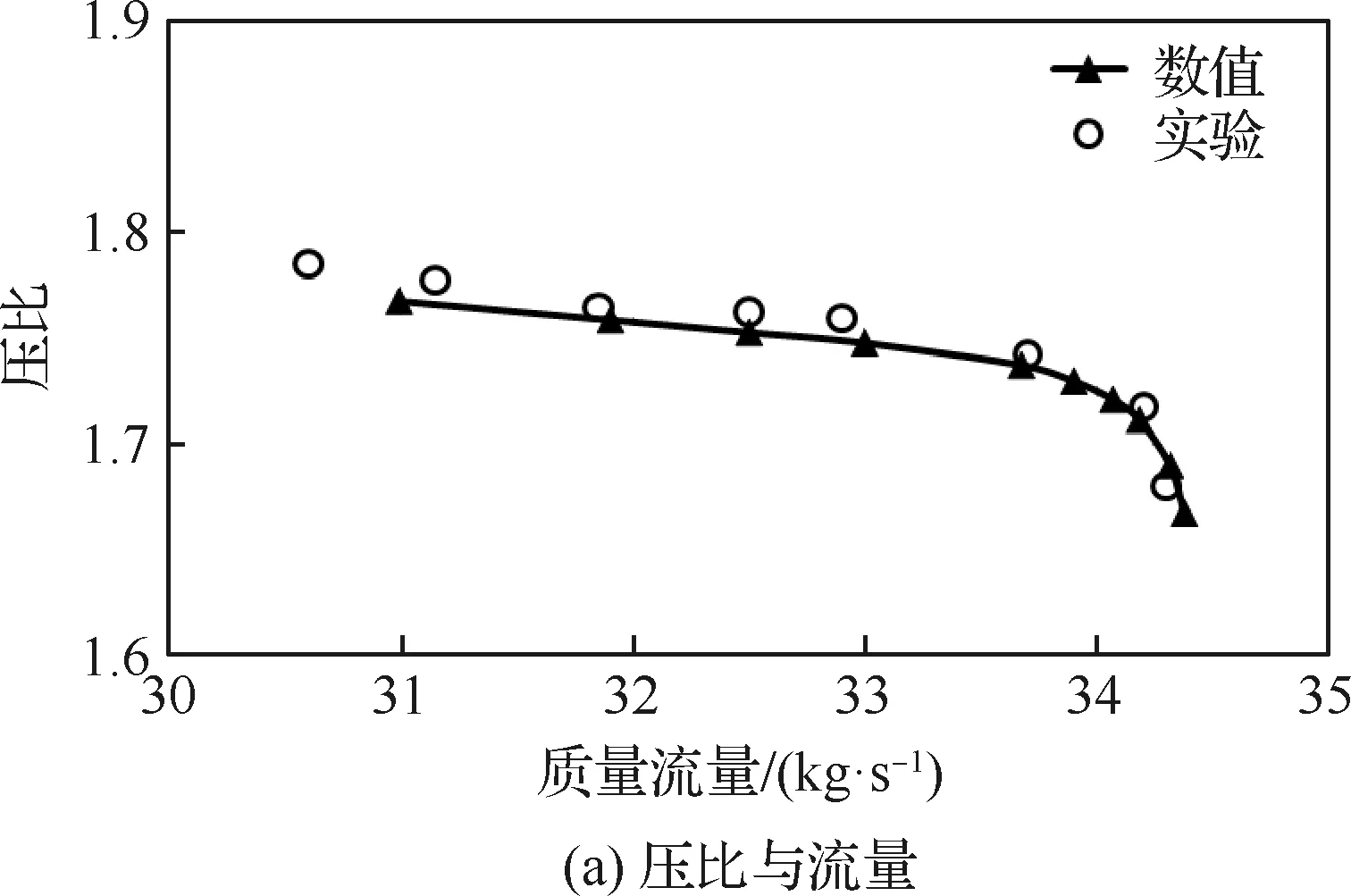
图4 实验与数值结果对比

其他参数不变，网格数量分别调整为31万、60万、122万、165万时，发现网格数量从81万开始后数值计算的偏差小于0.3%，网格数量为31万、60万时计算偏差分别为3.1%、1.2%，因此为保证网格无关性并节省计算时间，后续数值计算的网格数均选取为81万左右。

2.2 数值计算结果

27个正交实验的计算结果如图5所示。ΔQ、ΔP、Δη分别表示每个正交实验最高效率点的流量、总压比、效率偏离设计叶片的大小，即

(1)

式中：Q、P、η分别为流量、压比、效率的计算值，下标SM代表正交实验，下标D代表设计叶片。

从图5能看出，叶片的加工误差改变了压气机最高效率点的性能，压气机的性能并不总是比设计值减少，也有部分增加。

图5 正交实验计算结果分布图

表3为所有正交实验下压气机的总压比、效率、流量的极值。从表3可以看出加工偏差对性能影响较大，总压比、效率、流量增加的最大量分别为2.02%、1.47%、1.87%，减少的最大量分别为-0.87%、-1.42%、-0.88%。

表3 正交实验的极值

3 结果分析

3.1 极差分析

对图5的正交实验结果数据进行极差分析。27个实验分为3组，分组是按照每个参数的3个水平值来分的，对每个参数来说，分组方式是不一样的，正交实验法的设计能保证每个参数的每个水平值下，其他参数的综合影响都能全面考虑，因此结论具有较高的可信度，每组9个实验，求出每组的ΔQ、ΔP、Δη之和，极差即为每组ΔQ、ΔP、Δη之和的最大值与最小值之差，各参数的极差值对比详见表4。

表4 各参数的极差值对比

对于流量极差，ΔX1、S较大，其他值较小，表明前缘角偏差、前后缘形状对流量的影响较大，而后缘角偏差、弦长偏差、截面位置、厚度偏差对流量的影响相对较小。对于总压比极差，S、Δc、P较大，其他值较小，表明前后缘形状、厚度偏差、截面位置对总压比的影响较大，而后缘角偏差、弦长偏差、前缘角偏差对总压比的影响相对较小。对于效率极差，ΔX1最大，表明前缘角偏差对效率的影响最大，Δc其次，表明厚度偏差对效率的影响次之，其他值较小，表明后缘角偏差、截面位置、弦长偏差、前后缘形状对效率的影响较小。

图6～图11分别为各分组的前缘角偏差、后缘角偏差、前后缘形状、截面位置、弦长偏差、厚度偏差的趋势图，纵坐标值为各分组的ΔQ、ΔP、Δη之和。从图6可以看出，前缘角偏差为负时，流量明显升高，效率略有提高，总压比略有降低，前缘角偏差为正时，流量、效率明显降低，总压比略有降低，因此建议加工时前缘角尽量为负偏差。从图7可以看出，后缘角偏差为负时，效率、总压比、流量略有降低，后缘角偏差为正时，效率、总压比略有降低，流量略有提高，总体来看该参数对性能的影响很小。

图6 前缘角偏差趋势

图7 后缘角偏差趋势

图8 前后缘形状趋势

图9 截面位置趋势

从图8可看出，前后缘形状为圆、椭圆、钝边时，效率变化不明显，但是前后缘形状为钝边时，相比前后缘形状为圆形时，流量减少约10%，总压比增大约7%，表明最高效率点往小流量、高压比移动，改变了运行工况，因此建议加工时尽量避免前后缘形状由圆或椭圆变为钝边。

图10 弦长偏差趋势

图11 厚度偏差趋势

从图9可看出，以叶中的截面改变为基准，当叶顶处的截面改变时，总压比、效率有所增大，流量减少，叶根处的截面改变时，总压比、效率、流量变化不明显，表明叶顶位置相比叶中、叶根位置，对性能的影响更敏感，因此建议加工时，需严格控制叶顶位置的公差。从图10可看出，弦长偏差为负时，效率、流量没有明显变化，总压比略有提高，弦长偏差为正时，效率变化不明显，流量有所提高，总压比略有降低，总体来看该参数对性能的影响较小。从图11可看出，厚度偏差为负时，总压比、效率明显提升，流量略有提高，厚度偏差为正时，总压比、效率、流量变化不明显，因此建议加工时厚度尽量为负偏差。

3.2 回归线性分析

文献[19-20]有提到，对于较小加工偏差引起的性能变化，可认为是线性变化，考虑到截面位置的变化不会直接影响性能，因此本文对三维叶片的叶型前缘角偏差、后缘角偏差、前后缘形状、弦长偏差、厚度偏差这5个典型参数偏差综合作用进行了回归线性检验，在不同叶高处分别建立多元线性回归模型。以叶中位置为例，表5～表7为其回归方程的显著性检验表，其他位置处的多元线性回归模型构建与叶中位置类似，此处不再赘述。

表5 因变量为流量时的回归方程分析

表6 因变量为总压比时的回归方程分析

从表5可看出，因变量为流量时的回归方程的显著性系数小于0.01，表明回归方程高度显著，即加工偏差引起的流量变化可以用线性方程表示。从表6可看出，因变量为总压比时的回归方程的显著性系数大于0.1，表明回归方程不显著，即总压比变化与加工偏差之间不是线性关系。从表7可看出，因变量为效率时的回归方程的显著性系数小于0.05，表明回归方程是显著的，即加工偏差引起的效率变化可以用线性方程表示。因此在叶中位置处，对于本文提到的三维叶片的上述典型参数偏差综合作用引起的效率、流量变化，可认为是线性变化，但是引起的总压比变化，不能认为是线性变化。

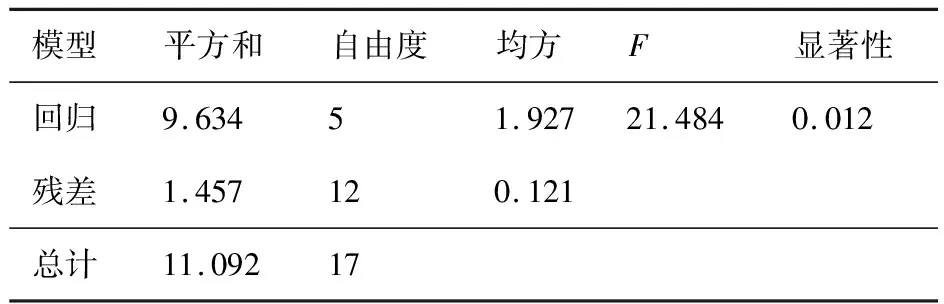
表7 因变量为效率时的回归方程分析

采用逐步回归法对叶型前缘角偏差、后缘角偏差、前后缘形状、弦长偏差、厚度偏差这5个典型参数偏差引起效率、流量变化的重要性进行分析，表8、表9为最终结果。

表8 因变量为效率时的回归系数

表9 因变量为流量时的回归系数

表8中前缘角偏差的标准化系数最大，显著性小于0.01，表明前缘角偏差是影响效率的最重要因素，厚度偏差的标准化系数次之，显著性小于0.05，表明厚度偏差也是影响效率的重要因素，其他因素对效率的影响都不显著。表9中前缘角偏差、前后缘形状的标准化系数较大，显著性均小于0.01，表明前缘角偏差、前后缘形状是影响流量的重要因素，其他因素对流量的影响都不显著。最终得出所构建的多元线性回归方程如式(2)和式(3)所示，这些分析结论与3.1节中极差分析的结果完全一致。

(2)

(3)

3.3 极值分析

对于跨声速压气机转子来说，叶片加工偏差的综合作用对压气机性能的影响较大，下面对压气机总压比、效率、流量这些性能参数的极值点与设计点的内部流动进行对比分析，以揭示出叶片加工偏差的综合作用影响压气机性能的机理。

表3中总压比的最小、最大值分别出现在序号为2和24的实验中，简写为Test2与Test24，图12为叶片出口1/2弦长处叶高的总压比分布图，从图12中可看出，Test2的总压比在整个叶高范围内都有所减少，在叶顶与叶中范围内减少较明显，Test24的总压比在整个叶高范围内都有所增加，在叶顶与叶中范围内增加较明显，表明叶片加工偏差引起的压力扰动能影响主流和顶部间隙流。图13为叶片99%叶高处的静压分布，从图13可看出在99%叶高处，Test24的压力面、吸力面压差较大，Test2的压差较小，受斜激波影响，吸力面在40%左右弦长处压力迅速升高，此时Test2的激波位置更靠近尾缘。

图12 总压比沿叶片展向分布

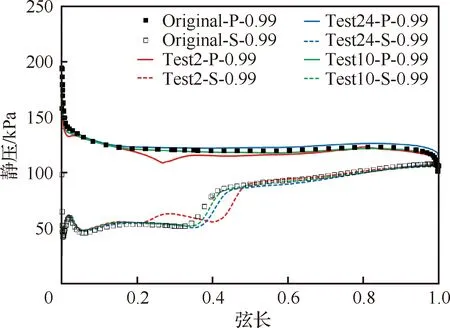
图13 99%叶高处压力分布

跨声速压气机叶片在叶尖处产生的激波与间隙泄漏、边界层等相互作用后对性能影响很大。图14、图15分别为Test2、Test24与设计叶片在叶尖泄漏流线、叶尖端壁压力分布图的对比。从图14可看出，黑线为泄漏流线，对于设计叶片，叶尖前缘的泄漏具有一定的周向速度，且受压力面、吸力面压差影响，在相邻叶片通道内向压力面流动，在尾缘处几乎贴近压力面，对于Test2，叶尖前缘的泄漏有少部分跨过相邻叶片叶顶间隙，流入相邻的第2个叶片通道，泄漏影响进一步增大，对于Test24的叶尖泄漏，受压力面、吸力面更大的压差影响，泄漏流动贴近压力面的程度减弱，泄漏影响受到抑制。从图15可看出，相比设计叶片，Test2的叶尖端壁压力有所减小，而Test24的叶尖端壁压力明显升高，也证实了Test24的泄漏影响最小，压比最高。图16～图18分别为Test2、Test24与设计叶片在99%叶高处的马赫数、熵分布图以及50%叶高处的马赫数分布图。从图16可以看出，在99%叶高处的流动较复杂，马赫数大于1.3的区域有两处，其中最大马赫数出现在吸力面弦长40%激波位置前，激波使吸力面边界层分离，和破裂的叶顶泄漏涡一起在吸力面后半弦长的通道范围内形成较大的低速区，阻塞了通道，减少通道流通能力，相比设计叶片，Test2在叶顶处流量较大，通道内马赫数增加，且最大马赫数影响区域较大，激波强度较高，与较大的泄漏涡混合后低速区的速度最低，压力损失较大，Test24在叶顶处流量较小，激波强度较小，影响区域小，压力损失较小。从图17可以看出，在99%叶高处Test2的熵增最明显，设计叶片次之，Test24的熵增最小，进一步证实了Test24的压力损失最小。从图18可以看出与图16中类似的结果，在50%叶高处，此处为主流区，Test2中激波较强，且其影响区域较大，Test24中最大马赫数影响区域较小，激波强度较低，因此在整个三维叶片中Test24的压力损失最小，效率最高。

效率的最小、最大值分别为Test10与Test24，图19为叶片出口1/2弦长处叶高的效率分布图，从图中可看出，Test10的效率在整个叶高范围内都有所减少，在叶顶与叶中范围内减少最明显，Test24的效率在整个叶高范围内都有所增加，在叶顶与叶中范围内增加最明显，表明叶片加工偏差引起的扰动能影响主流和顶部间隙流，进而影响叶片效率。前面已经对Test24进行了分析，下面仅对Test10进行分析。从图13可看出，Test10的压力面、吸力面压差小于设计叶片，吸力面上的激波位置相比设计叶片更靠近尾缘，抑制泄漏流动的能力有限。图20为Test10在99%叶高和50%叶高处的马赫数分布图，和图16、图18中的设计叶片马赫数分布相比，Test10在99%叶高和50%叶高处的马赫数较高，在吸力面激波前的最高马赫数达1.63，激波强度较高，激波与间隙泄漏、边界层等相互作用后对性能影响更大，在50%叶高处的高Ma流动导致较大的流动损失，同时吸力面激波较强，影响区域较大，因此效率最低。

图14 叶尖泄露流线

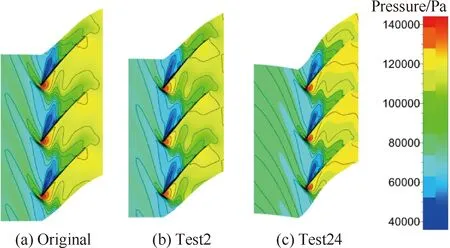
图15 叶尖端壁压力

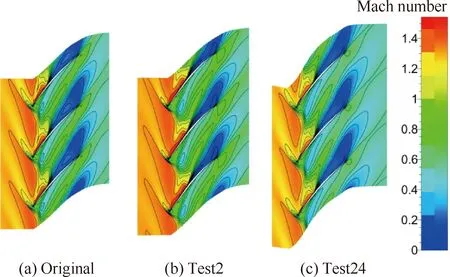
图16 99%叶高处马赫数分布

图17 99%叶高处熵分布

图18 50%叶高处马赫数分布

图19 效率沿叶片展向分布

流量的最小、最大值分别为Test5与Test19， 图21为叶片进口和叶片出口1/2弦长处叶高的轴向速度分布图，从图中可看出，叶片进口轴向速度为均匀分布，其中Test5在叶顶处前缘角增加会减少流量，由于前后缘为钝边，为了减少附面层对性能的不利影响，在最高效率点的流量有所减少，和设计叶型相比，Test5中叶片进口、出口轴向速度在整个叶高范围内都有所减少导致流量最小，Test19在叶根处前缘角减少会增大流量，由于前后缘为圆，在最高效率点的流量有所增加，和设计叶型相比，Test19中叶片进口、出口轴向速度在整个叶高范围内都有所增加导致流量最大。

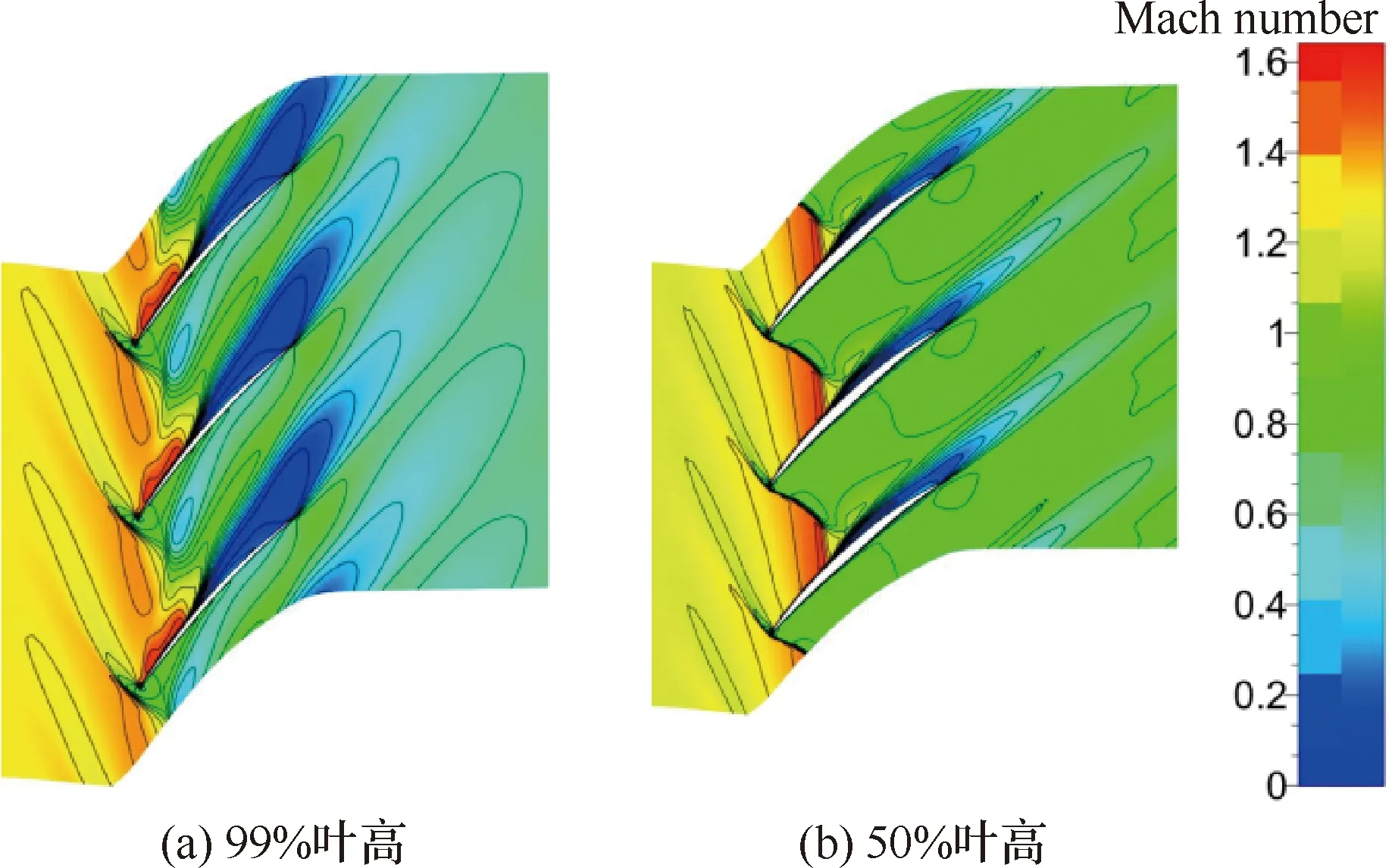
图20 Test10的Ma分布

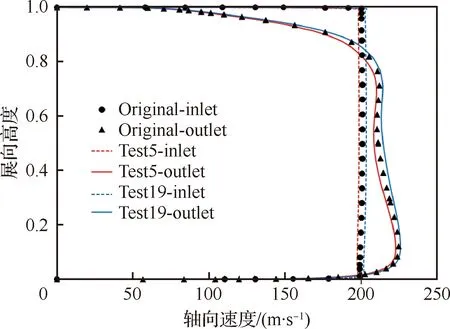
图21 轴向速度沿叶片展向分布

4 结 论

1) 三维叶片的上述6个典型参数偏差综合作用对压气机的总压比、效率、流量影响较大，其最大提升量分别可达2.02%、1.47%、1.87%，最大减少量分别可达-0.87%、-1.42%、-0.88%。

2) 三维叶片的上述6个典型参数偏差综合作用中，前缘角偏差、厚度偏差对压气机效率变化的影响较大，加工时前缘角、厚度尽量为负偏差；前后缘形状、厚度偏差、截面位置对总压比变化的影响较大，加工时尽量避免前后缘形状由圆或椭圆变为钝边，同时叶顶位置相比叶中、叶根位置对性能的影响更敏感，加工时需严格控制叶顶位置的公差；前缘角偏差、前后缘形状对流量变化的影响较大，其他参数如叶型后缘角偏差、弦长偏差对性能变化的影响较小。

3) 采用回归线性分析方法证实了三维叶片的上述典型参数偏差综合作用对效率、流量的影响是线性变化，对总压比的影响不是线性变化。