BLP模型发展及其在产业组织应用综述

一 引 言

“供需”分析长期以来一直是实证经济学的主要研究内容。在产业组织理论问题的实证研究中，传统的简约式分析方法侧重于分析变量之间的因果关系，无法清晰地辨别问题背后的变化机理，从而影响其在政策评估、福利分析中的应用。为了克服简约式分析的缺陷，新实证产业组织的研究范式应运而生。而在新实证产业组织研究范式中，BLP模型是目前应用最为广泛的研究方法之一， BLP模型可以进行需求侧和供给侧估计，更加明确地回答研究中存在的假设性问题(王子和周雁翎，2019)[1]，清楚分析问题的内在机理，并通过反事实分析得出合理的政策评估结果。

早期的实证分析是在不完全竞争市场下进行同质化产品市场的需求和成本函数估计。由于产品数量少，此类模型易于处理。随着市场假设和研究方法的不断发展，经济学研究对象越来越倾向于特定行业以及替代性产品。人们逐渐意识到对于差异化产品市场研究的重要性。McFadden(1974)[2]等提出的离散选择模型解决了差异化产品需求估计的问题。该模型从一类消费者行为推导出市场需求。由于消费者效用依赖于产品特征和消费者的偏好参数，最大化消费者效用并根据消费者决策加总的结果获取消费者对该产品的选择概率，将其近似为产品层面的市场份额，从而估计出需求函数系数。该方法有两个优点：一是解决了维数过多的“参数诅咒问题”；二是可以对新产品进行反事实模拟。但离散选择模型在研究过程中对于产品全部特征没有要求，忽视了不可观测的产品特征，这些不可观测的产品特征可能与价格变量之间存在内生性问题，而忽视内生性问题会导致估计的需求曲线向上倾斜，带来估计结果误差。另一方面，在数据要求上，McFadden(1974)[2]的离散选择模型需要个体层面的数据，而对于研究人员来说个体层面的数据难以获取，在实践中为问题研究带来了困难。上述问题的存在限制了离散选择模型的应用。

为了解决离散选择模型的局限性，在McFadden(1974)[2]研究的基础上，Berry et al.(1995)[3]利用销量、价格、产品特征等数据提出了差异化产品市场的需求估计方法——随机系数Logit模型(BLP模型)，该模型克服了离散选择模型的缺陷，充分考虑到价格与不可观测的产品特征之间的内生性问题，利用聚合的产品层面数据完善了早期离散选择模型对于个体层面数据的限制，并且解决了维数诅咒问题以及产品特征的异质性问题。随后，BLP模型被广泛应用于产业组织实证问题研究中，结合严谨的理论模型、最大化效用函数以及利润函数的思想将实证模型结构化并运用到实证研究问题中，使估计结果更加贴近现实，以进一步解释产业组织理论问题的内在机理。Nevo(2000)[4]详细解释了BLP模型。此后，BLP模型被具体应用于差异化产品市场的市场势力、并购、创新、投资广告决策、定价、消费者福利估计以及规制政策分析等产业组织理论问题的实证研究中。

BLP模型是产业组织理论问题实证研究的有力工具，具体应用中有如下优势：(1)数据要求并不严格；(2)可以根据消费者偏好构建效用函数合理估计出需求函数，利用供给侧函数估计出边际成本参数，从而根据现实中产业链上下游的纵向关系、企业之间的竞争等互动行为建立符合现实的模型；(3)可以清楚分析出研究框架中各个因素的影响效果，而不是仅得出因果之间的正、负向影响；(4)政策效果的评估针对性强，可以通过反事实分析评估不同政策环境下的政策效果；(5)可以进行福利分析，根据反事实模拟分析不同政策环境下的福利效应。

近年来，关于BLP模型应用和方法的研究受到学者关注。随着对BLP模型研究的不断深入，越来越多学者发现BLP模型仅适用于非耐用品市场，没有考虑到耐用品市场中消费者长期效用对于消费者购买决策的影响，而前瞻性消费者可能会根据未来产品供应和价格的预期改变购买决策。因此对于BLP模型的研究从非耐用品市场发展到耐用品市场和半耐用品市场(Goettler和Gordon，2011[5]；Gowrisankaran和Rysman，2012[6])，在效用函数中充分考虑消费者预期，建立贝尔曼方程估计需求函数,使模型设定更加符合现实情况，估计结果更加精准。在前沿的BLP模型方法研究中，主要关注三个方面问题：首先是对于方法中市场份额积分的近似运算进行优化；其次是关于模型构建过程中非线性系统的数值算法优化研究；最后是对于估计方法的研究。

目前关于BLP模型的应用研究逐渐从传统的产业组织问题研究发展到双边市场理论问题的实证研究以及更广泛的领域中，BLP模型的构建方法也不断改进，将需求侧由静态的随机系数Logit模型发展为动态需求模型，与EP模型(Ericson和Pakes，1995)[7]结合，构建供给侧动态结构模型，并且应用范围逐渐向其他经济学与管理学领域拓展(刘忠等，2012)[8]。而国内关于BLP模型的实证研究及应用较少，因此本文拟简要介绍BLP模型的原理、发展、模型特点和优势，以及其在产业组织领域的应用。

二 BLP模型的基本原理及发展

自Berry等提出BLP模型以来，关于BLP模型的研究主要集中在模型的构建、算法优化以及估计方法选择问题中。本文提出的BLP模型主要参考了Reynaert和Verboven(2014)[9]的模型构建过程，通常由以下步骤组成：(1)建立消费者的效用函数，并设定待估计参数；(2)通过博弈理论构建供给侧模型以及待估计参数；(3)运用数据估计需求函数与供给函数中的需求参数以及边际成本参数；(4)根据不同情景进行反事实模拟分析。本文从需求侧函数、供给侧函数以及估计方法三个方面介绍BLP模型构建的基本原理。

(一)需求侧函数

假设存在t=1,2,…,T个市场，可以观察到产品J的总体销量、平均价格以及产品特征。存在Lt个潜在消费者，每个消费者i(i=1, 2, …,Lt)会选择替代性产品j,其中外部产品为j=0,差异性产品表示为j=1,2,…,J，消费者对于外部产品的间接效用为：μi0t=εi0t，消费者i在市场t购买产品J的间接效用为：

Uijt=xjtβi-αpjt+ξjt+εijt

(1)

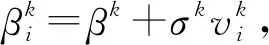
(2)

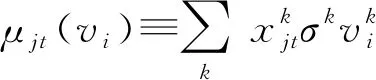
Ajt={(α,β,σ,εijt)|Uijt≥Uist,j≠s,j,s∈J}

(3)

消费者i选择市场t中产品j的概率pijt为：

pijt=P(Uijt≥Uist,j≠s,j,s∈{0,1,…J})

(4)

因此有：

(5)

在市场t中产品j预测的市场份额是指产品j在所有可用产品(包括外部产品j=0 )中产生最高效用的概率。通过对个体特定评价进行积分可以得出：

(6)

其中Vijt中包括平均效用参数向量α和β以及平均评价值的标准差向量σ，令θd=(α,β,σ) 。

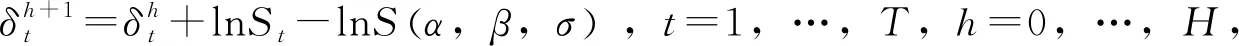
目前市场份额的近似计算通常采用两种方法，一种是采用蒙特卡罗模拟求解积分：

(7)

另一种方法是采用基于多项式的稀疏网格方法(Heiss和Winschel，2008)[10]近似求解积分:

(8)

Skrainka和Judd(2012)[11]在BLP模型的研究背景下利用MPEC算法检验了两种积分方法的效果，证明了基于多项式的稀疏网格方法在效率和优越性方面优于蒙特卡罗方法，蒙特卡罗方法在计算过程中可能产生数值误差且存在不稳定性，而稀疏网格方法解决了这种问题，使计算结果更加高效。

(二)供给侧函数

假设产品j在市场t中的边际成本是常数，且表示为：

cjt=xjtγ1+wjtγ2+ωjt

(9)

其中xjt是产品特征向量，既影响效用又会影响成本，wjt是只影响边际成本的其他因素向量，ωjt是不可观测的边际成本影响因素。由于边际成本难以获取，但可以通过供给模型估计出来，在完全竞争条件下，价格等于边际成本，即pjt=cjt，因此有：

pt=xtγ1+wtγ2+ωt

(10)

不完全竞争条件下，BLP模型采取伯川德竞争，每个企业f会设定价格使其达到利润最大化结果，因此，纳什均衡的一阶条件是：

(11)

在不完全竞争条件下，由供给侧可以得出：

(12)

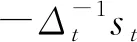
(三) GMM估计

构建需求侧与供给侧模型后进行参数估计。而对于BLP模型的估计主要有两个问题：(1)通过聚合的市场份额系统解决需求函数参数以及边际成本参数估计问题；(2)通过广义矩估计(GMM)方法选择工具变量估计参数。

由于变量之间具有内生性以及非线性的市场份额系统问题，BLP模型估计通常采用GMM方法，条件矩限制为：

E[ρjt|zt]=0

(13)

其中，ρjt=(ξjt,ωjt)′和zt=(Xt,Wt)。

用非条件矩限制条件表示：

E[gjt(zt)ρjt]=0

(14)

其中，gjt(zt)是由外生数据zt的任意函数组成的q×2阶矩阵。

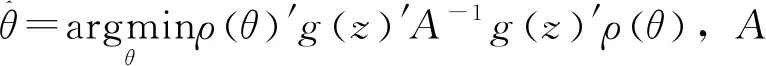
Berry et al.(1995)[3]利用NFP算法解决最小化问题：外部循环通过最小化目标函数，内部循环利用压缩映射解决。然而，NFP算法存在一定的缺陷，GMM方法需要在非线性系统中搜索局部最小值，通过压缩映射搜索参数值，由于在GMM估计内循环中NFP需要循环上百次甚至上千次，会导致计算成本过高，为了解决这个问题，通常会选择较大阈值以减少循环次数，这种方式虽然可以减少计算时间，但会使估计结果产生误差。Knittel和Metaxoglou (2014)[12]指出在使用BLP方法的过程中，优化方法可能不会达到局部最小值，并且获得的局部最小值可能不是全局最小值，由于具有高度的非线性，局部最小值之间的差异会造成估计结果的差异。因此需要选择多个初始值以获取参数空间的全局最小值，但这种方法会增加计算成本(Kim et al.，2017)[13]。

为了解决NFP算法存在的缺陷，Dubé(2012)[14]提出了新的算法——具有平衡约束的数学规划(MPEC)，以优化GMM方法，使规划问题转化为受到市场份额约束的最小化GMM目标函数问题：

minρ(θ)′g(z)′A-1g(z)′ρ(θ)

(15)

s.t.s(α,β,σ)=s

同时比较NFP与MPEC的精确度和收敛速度，结果表明MPEC没有嵌套内部循环，不存在内部循环误差，避免了收敛点不是局部最小值的缺陷；消除了具有内部循环的压缩映射问题，使收敛过程更快。与Berry et al.(1995)[3]的方法相比，MPEC完全消除内部循环问题，从而消除估计不准确的可能性，估计过程消耗时间更少且不需要压缩映射，更适用于一般的需求模型估计。

GMM估计中的另一个问题是工具变量的选择，Reynaert和Verboven(2014)[9]认为使用Chamblain(1987)[15]的最佳工具可以解决BLP模型中许多非最优工具问题。最优工具不仅减少了小样本偏差，提高估计量的效率(均方误差)和稳定性。同时使用MPEC和最优工具可以提高优化问题的计算速度，而且基于多项式的稀疏网格方法对市场份额积分，在效率和计算速度方面优于蒙特卡罗积分方法。

除了GMM估计外，Park和Gupta(2009)[16]提出了SML估计方法，并比较了SML方法与GMM方法(Park和Gupta，2012)[17]，结果表明SML估计在恢复异质性参数方面优于GMM估计。与GMM方法相比，使用SML估计更加有效。

(四)BLP模型研究的最新进展

近年来，一些研究试图改进BLP模型，由于BLP模型需要依靠数值方法解决，Lee和Seo(2015)[18]基于BLP模型和一个线性近似市场份额函数提出了计算速度更快的随机系数Logit模型估计方法，称为近似BLP模型(ABLP)。与BLP模型相比，该方法可以通过解析的方法反演市场份额方程而不是利用数值求解方法，ABLP解出市场份额方程具有唯一的最优解，相比其他方法计算速度更快。Moon et al.(2018)[19]扩展了BLP模型中的随机系数离散选择需求模型，在不可观测的产品特征上以因子结构的形式添加交互式固定效应。交互式固定效应可以与观察到的产品特征任意相关，同时提出了两阶段最小二乘最小距离(LS-MD)方法来进行估计，通过蒙特卡罗模拟证明估计方法具有较好的性质。

已有BLP模型研究大多依赖于静态需求模型，然而在现实市场中需求模型多为动态，例如：消费者当前的决策会影响未来的效用；消费者当前的决策取决于对未来发展的预期。BLP模型由于忽视在耐用品市场中具有前瞻性消费者的长期效用，仅适用于非耐用品市场，在耐用品市场中运用BLP模型进行需求估计可能会使估计结果产生偏差。消费者对产品未来价格和供应的期望也影响当前购买与未来购买之间的权衡。因此，在需求估计过程中，采用静态需求模型而忽略动态因素会导致偏差和不一致估计(Aguirregabiria和Nevo，2010)[20]。Gowrisankaran和Rysman(2012)[6]、Goettler和Gordon(2014)[21]、Ishihara和Ching(2019)[22]构建了基于消费者预期的动态需求模型。当前，产业组织问题的实证研究中，动态结构模型结合BLP模型构建思想，通常以EP研究框架为基础，构建供给侧模型(Pakes，2000[23]；Gowrisankaran和Town，1997[24])，充分考虑到竞争主体的异质性、竞争行为的策略性以及竞争过程的随机性，并且可以合理描述动态寡头市场的市场特征。Su和Judd(2010)[25]、Su(2014)[26]以及Egesdal et al.(2015)[27]等分别给出动态结构模型中需求侧与供给侧函数的估计方法。

三 BLP模型的特征分析

BLP模型从微观经济学中消费者效用最大化出发，通过最大化的消费者效用以及企业行为解释经济学现象。与传统的实证方法不同，BLP模型以估计需求曲线为基础，在数据选取、模型构建以及应用范围都具有较大优势，可以进一步检验经济行为假设，尤其适用于产业组织理论问题的研究。

(一)BLP模型的特点

BLP模型的优势首先体现在数据选取上。McFadden(1974)[2]的离散选择模型通常需要消费者的个体选择数据，然而在现实应用中，研究人员难以获取消费者的个体选择数据，而BLP模型不需要消费者个体的购买决策数据，通过对消费者分布进行积分，结合产品选择概率，利用市场份额数据构建需求函数，从而可以依靠市场层面的数据进行研究。因此BLP模型对于数据的要求并不严格，仅需要产品的销量以及价格数据。

在BLP模型构建过程中，充分考虑到如下问题：首先是价格的内生性问题，由于未观测到的产品特征可能会与产品价格相关，Berry et al.(1995)[3]在模型中考虑到了研究人员未观测到的产品特征与产品价格之间可能存在内生性问题，并通过GMM估计解决这种内生性问题；其次，考虑到差异化产品市场，BLP模型不再局限于同质产品市场研究，使研究对象更加丰富；最后，考虑到消费者的异质性问题，消费者个体选择存在差异，BLP模型通过对消费者特征分布进行积分解决消费者异质性问题。

BLP模型以需求侧模型与供给侧模型为基础构建实证模型展开研究。而需求侧与供给侧模型是从经济学理论中抽象出来，与简约式模型不同，BLP模型并不是从数据中分析变量之间的因果关系，其关键特征是紧密联系理论框架和现实数据，估计得到的参数结果更加稳定。BLP模型可以在估计出需求参数的基础上，以理论模型为基础构建供给侧模型，并以此为研究框架进行不同情境下的反事实模拟分析，从而进行政策评估、福利分析。

(二)BLP模型的优势分析

在已有的实证过程中发现BLP模型具有如下优点：(1)数据要求并不严格。可以根据消费者偏好构建效用函数，合理估计出需求函数，利用博弈论、通过建立供给侧函数估计出边际成本，从而得到产品的边际成本函数，进一步分析研究框架中各个因素的影响效果，而不是仅得出因果之间的正、负向影响；(2)政策效果的评估针对性强，可以通过反事实模拟，在不同政策环境下评估政策效果，分析均衡结果的变化，这一方法可以分析简约式方法估计结果无法解释的背后原因；(3)通过企业不同的定价策略可以进行福利分析，根据反事实模拟分析不同政策环境下的福利效应。

随着BLP模型逐渐从静态结构模型发展为动态结构模型，其优势进一步显现，主要体现在：(1)构建需求侧函数时，通常情况下前瞻性消费者会考虑到耐用品、半耐用品的未来价格以及长期效用，根据未来产品供应和价格的预期改变购买决策，动态结构模型设定更加贴近现实情况，需求函数的估计结果更加精准。(2)而对于供给侧模型，企业间的动态竞争、投资、广告、研发等通常会使企业在当前与未来决策之间取舍。考虑到市场发展趋势以及对竞争对手行为的预期，企业之间的竞争决策、策略互动以及随机的市场冲击都会对市场演化造成影响，因此动态结构模型可以更好地刻画现实市场情景。

BLP模型的不断优化发展，使其可以用来构建越来越符合现实的实证模型，虽然现如今BLP模型已经发展到动态结构模型，但由于动态结构模型相比BLP模型算法更加复杂，在实际的应用中，可能会导致更高的计算成本，需要根据产品市场的具体情况、获取数据的样本期长短以及具体的研究问题来合理地选择模型，避免造成计算成本过高。

四 BLP模型在产业组织理论中的应用

近年来，BLP模型在产业组织领域实证研究中应用得越来越多。不同于传统产业组织领域实证研究较常采用的简约式分析模式，BLP模型不需要控制多个变量，可以通过效用函数估计需求系数，根据产业组织理论研究模型估计边际成本系数，并进行供需分析。因此，BLP模型更适用于产业组织领域中评估、识别策略效应，通过反事实模拟分析不同市场环境下企业策略的作用机理。

(一)纵向策略识别

关于纵向关系和纵向约束的相关研究多采用理论模型框架，且相对成熟，但实证研究仍然较少，在简约式分析中通常采用虚拟变量来衡量纵向合约(Chen和Shieh，2016)[28]。简约式分析方法仅能通过构建指标研究自变量与因变量的因果关系，无法有效识别企业纵向控制手段。而运用BLP模型来构建实证模型，通过反事实模拟对不同纵向控制手段进行实证分析则可以克服这一缺陷。

Lee(2013)[29]衡量了平台的纵向一体化和具有排他性的软件对于美国视频游戏产业结构和福利的影响，分别估计了消费者对于硬件和软件产品的需求以及硬件平台对软件需求的动态结构模型。由于视频游戏具有耐用性，需要在需求侧建立动态需求模型，并在硬件效用函数模型中添加硬件拥有量，结果表明硬件平台与软件开发商之间的一体化和独家合约有助于平台进入。在平台市场允许强制排他性合约的情况下，监管部门没有必要进行干预和监督。反事实模拟禁止排他性合约情境，结果表明虽然禁止排他性合约后行业更加集中，但消费者仍然可以从每个平台的软件中获益。Yang(2017)[30]构建上下游创新的动态模型研究了智能手机与芯片产业纵向一体化的创新效应，首先根据消费者效用函数构建了随机系数Logit模型，再以时间、产品质量以及一体化程度作为状态变量分别构建智能手机与其上游芯片的动态模型，模拟上下游不同一体化程度的市场结构，表明纵向一体化以及一体化企业之间的协调投资可以增强创新效率和社会福利。

Bonnet et al.(2013)[31]考虑了在上游面临成本冲击时，企业通过实施非线性定价和纵向约束(如转售价格维持、批发价格歧视)调整加价策略的影响。利用结构模型方法研究认为，非线性定价合约和纵向约束对于产业链的影响可以起到调整上游成本冲击的作用。通过对比转售价格维持与线性定价，解释上游成本冲击到下游零售价格的传递程度。Bonnet和Dubois(2010)[32]提出了一个结构模型的实证研究框架，考察制造商和零售商之间的两部收费制合约，估计非线性两部收费制合约的结构模型是否存在转售价格维持，在寡头垄断环境下检验上、下游不同的纵向合约模型。估算需求参数后在非线性合约模型中恢复总边际成本，然后通过改变生产和分配的边际成本的外生变量进行检验。实证分析结果表明，制造商和零售商将使用非线性定价合约，特别是带有转售价格维持的两部收费制合约。Li和Moul(2015)[33]分析了中国手机市场制造商与零售商之间的纵向合约和消费者服务对企业利润和社会福利的影响。根据制造商与零售商纵向合约由线性定价转换为收益共享合约分别建立供给侧模型，表明企业之间的纵向合约转换和由制造商承担零售商服务可以改善客户服务，从而提高消费者福利。反事实分析表明制造商在提供高质量服务时与零售商相比具有更大的成本优势。

国内对于BLP模型的研究和应用相对较少，主要集中在纵向关系的实证研究中。肖俊极和谭诗羽(2016)[34]检验了中国乘用车行业普遍存在的上下游纵向一体化关系以及由此引发的横向共谋行为，利用随机系数Logit模型刻画消费者选择，提出共同代理理论下四种乘用车市场竞争结构假设，实证结果表明同一外方母公司参股的合资企业，如果它们的关键零部件均由外方母公司纵向一体化供给，则它们之间存在共谋。参与共谋的合资企业利润不仅明显高于自主品牌企业，也高于其他合资企业。李凯和赵伟光(2018)[35]以中国乘用车市场纵向价格垄断案为背景，对整车制造商实施转售价格维持是否弱化下游竞争进行实证检验，通过对不同的纵向策略构建供给侧模型分析社会福利。结果表明上游整车企业为了避免下游4S店价格竞争引发的负外部性，通过实施转售价格维持，消除或弱化下游产品横向竞争，最终实现垄断定价。

(二)水平兼并审查

水平兼并通常以市场集中度作为衡量指标，但这种衡量方法不适用于差异化产品研究。而BLP模型可以估计出差异化产品的需求。Nevo(2000)[4]利用结构模型提出了模拟价格均衡的方法：首先估计了差异化产品的需求函数，接下来根据供给侧模型估计了边际成本参数，最后通过计算新的均衡模拟兼并影响。其运用这一方法进一步模拟即食谷物行业兼并所带来的价格变化，同时检验四种不同兼并带来的社会福利影响。Fan(2013)[36]考虑了内生的产品选择和价格选择问题，研究明尼阿波利斯报纸市场兼并的影响，并分析兼并的福利效应如何随市场特征变化而变化。结果表明，忽视产品特征的调整会导致估计结果产生重大差异。Gowrisankaran et al.(2013)[37]构建医院与管理式医疗机构(MCO)之间竞争的讨价还价模型，并评估医院兼并的影响，结果显示MCO讨价还价会显著抑制医院价格，同时发现北弗吉尼亚州的医院兼并会显著影响医院价格。Miller和Weinberg(2017)[38]对美国酿酒行业MillerCoors合资企业兼并后的经济影响进行实证调查，对兼并发生后MillerCoors及其主要竞争对手Anheuser-Busch的零售啤酒价格突然上涨原因进行经济分析。在一个差异化产品定价模型的背景下构建结构模型，反事实模拟表明兼并会带来价格协调效应，弱化兼并企业与其竞争对手之间价格竞争的激烈程度。

(三)市场结构与企业创新

针对市场结构与企业创新的实证研究，多采用简约式分析考察企业的创新绩效(孙晓华和郑辉，2011)[39]。在实证研究过程中，简约式分析通常需要外生控制多个变量，并且没有考虑到企业的策略性行为。因此，利用简约式分析不足以合理地解释影响企业创新绩效的内在机理。而通过以BLP模型为基础的动态结构模型可以充分考虑竞争主体之间的异质性、竞争行为的策略性以及竞争过程的随机性，构建更加灵活的模型研究企业的创新绩效问题，并且减少人为设定，使研究结果更为稳健。

与简约式分析方法相比，结构分析方法可以考虑到市场结构的内生性以及创新与市场结构之间的关系。Goettler和Gordon(2011)[5]估计了具有内生创新的耐用品的动态寡头垄断模型，讨论市场结构和产品质量演变之间的关系。企业考虑消费者对于产品质量提升和价格下降的动态反应，做出动态定价和投资决策。考虑耐用品以及内生的长期创新率，对电脑处理器产业进行估计，并通过反事实模拟分析竞争的效应。结果表明，当市场趋于垄断时消费者剩余会提升。Goettler和Gordon(2014)[21]研究了寡头垄断的市场结构下竞争和企业创新之间的关系，考察了竞争的决定性因素对企业均衡策略的影响。结果表明产品替代性和创新之间呈倒U型关系，倒U型曲线中上升部分反映了企业投资策略函数的变化，而下降部分表明当企业数量减少时产品质量差距变化。市场结构内生化与固定或外生给定市场结构会产生不同结果。Hashmi和Biesebroeck(2016)[40]分析全球汽车行业的动态博弈，通过计算马尔可夫均衡，研究汽车行业市场结构与创新之间的均衡关系。结果表明汽车行业中领导企业的创新会降低其他企业的创新效率，使创新效率更加集中，导致领导企业和其他企业之间的创新差距随着竞争强度的增加而增加。

(四)市场势力的测度

市场势力的衡量指标主要有勒纳指数、市场集中度、企业数量。勒纳指数的构建需要边际成本数据，然而这在实证研究中较难获取，市场集中度与企业数量则无法用来衡量特定企业的市场势力。周末和王璐(2012)[41]采用新实证产业组织研究范式测度了白酒行业的市场势力与垄断损失，但该方法没有考虑到消费者效用和产品特征，可能会造成市场势力估计误差。而BLP模型不仅可以估计企业的边际成本用于测度市场势力，同时还充分考虑到消费者偏好以及产品特征。这一分析框架容纳了不可直接观测的外部环境、潜在竞争等诸多因素，从企业行为出发，克服了传统方法在市场势力测度上的缺陷。

Nevo(2001)[42]实证检验了即食谷物行业的定价行为和非价格竞争行为，并将影响勒纳指数的因素分为差异化产品、多产品企业定价、潜在价格合谋三个方面进行讨论。结果表明即食谷物行业的价格与非竞争性定价行为一致，领导企业可以维持差异化产品，并且影响对于产品质量的预测，由此导致了较高的勒纳指数。Draganska et al.(2010)[43]通过考虑消费者需求以及均衡模型中制造商和零售商之间的互动，分析渠道利润的决定因素和渠道相对势力。其模拟了制造商和零售商之间的谈判，通过构建一个纳什讨价还价的博弈模型，以确定批发价格，并将模型应用于德国咖啡行业分析。结果表明不同制造商与零售商之间的议价能力不同，企业规模是决定讨价还价能力的关键因素。李凯和赵伟光(2018)[44]运用新实证产业组织研究范式构建中国乘用车市场的结构模型，对合资企业整车制造商中资议价势力进行实证研究，为政府部门制定中国乘用车行业产业政策提供参考。

除此之外，BLP模型还应用于新产品引入(Waldfogel和Berry，1999[45]；Nevo，2003[46]；Carranza，2010[47])、投资广告决策(Anand和Shachar，2011)[48]、产业政策审查(Beresteanu和Li，2011)[49]等领域。总结国内外关于BLP模型在产业组织领域的实证研究应用可以看出，越来越多的产业组织问题实证研究采用结构式分析方法。BLP模型可以根据企业的行为构建不同供给模型，对不同企业策略进行预测分析，从而更加合理地分析经济问题。而在传统产业组织问题的实证研究中，无法深入探讨企业策略以及其产生的经济效果，BLP模型的出现恰好可以解决实证研究在这一方面的缺陷。因此，BLP模型在产业组织领域的实证研究中具有重要的应用价值。

五 主要结论及未来研究展望

本文系统梳理BLP模型的原理、算法研究进展及其扩展，同时回顾了其在产业组织领域的应用。BLP模型将理论模型构建思想与实证模型相结合，利用理论模型的研究范式结合实证方法估计需求与供给函数。通过最大化消费者效用建立需求估计模型，根据博弈理论建立供给模型，从而建立结构模型进行经济学分析。但由于BLP模型的算法复杂性，需要清楚了解其原理。从模型应用角度来看，BLP模型不局限于传统产业组织问题的实证研究，同时适用于平台等新兴产业组织理论问题研究。从方法论上看，近年来产业组织领域的实证研究更倾向于结构式分析方法；比较传统实证方法与结构模型方法可以看出，BLP模型的应用使实证分析不再局限于因果关系，同时可以兼顾消费者选择与企业行为，对不同企业策略进行预测和识别，从而合理地分析和解释经济问题。现阶段，国内利用结构模型分析产业组织理论问题的研究较为丰富，但对于该方法的研究和应用比国外要少得多，因此应该根据BLP模型的应用范围，结合国内产业组织热点问题，拓展该模型的应用。

BLP模型正逐渐从产业组织理论的实证研究向其他经济学、管理学领域延伸，未来对于BLP模型的研究无论是算法优化还是应用研究均会有较高的意义和价值。因此，本文认为BLP模型的未来研究可以从如下两个方面展开：

第一，从方法角度上看，提高模型的计算效率是关键所在，也是难点所在。随着BLP模型逐渐从静态结构模型发展为动态结构模型，其算法的复杂性亦相应增强。目前关于模型的算法研究较多，但市场份额的数值积分方法、估计算法的精确性以及算法收敛程度问题仍然有待解决；由于BLP模型采用数值解的形式，因此可以考虑以解析解方式改进模型；有关BLP模型的估计方法选择也是一个有待深入讨论的问题。

第二，从应用角度上看，BLP模型的应用范围不再局限于传统产业组织理论问题的实证研究，更适用于双边市场理论的实证研究。目前关于互联网背景下产业组织理论问题的实证研究较少，由于BLP模型是在聚合的消费者选择的基础上构建，可以考虑结合BLP模型和Python等软件研究互联网背景下的新兴产业组织理论问题。