面积问题中三角形动顶点的求法探索
2020-03-24黄斌
数学学习与研究 2020年26期
黄斌
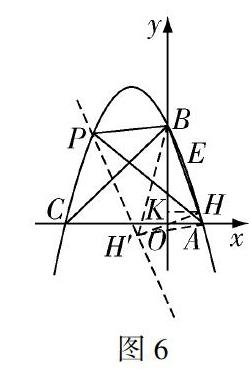
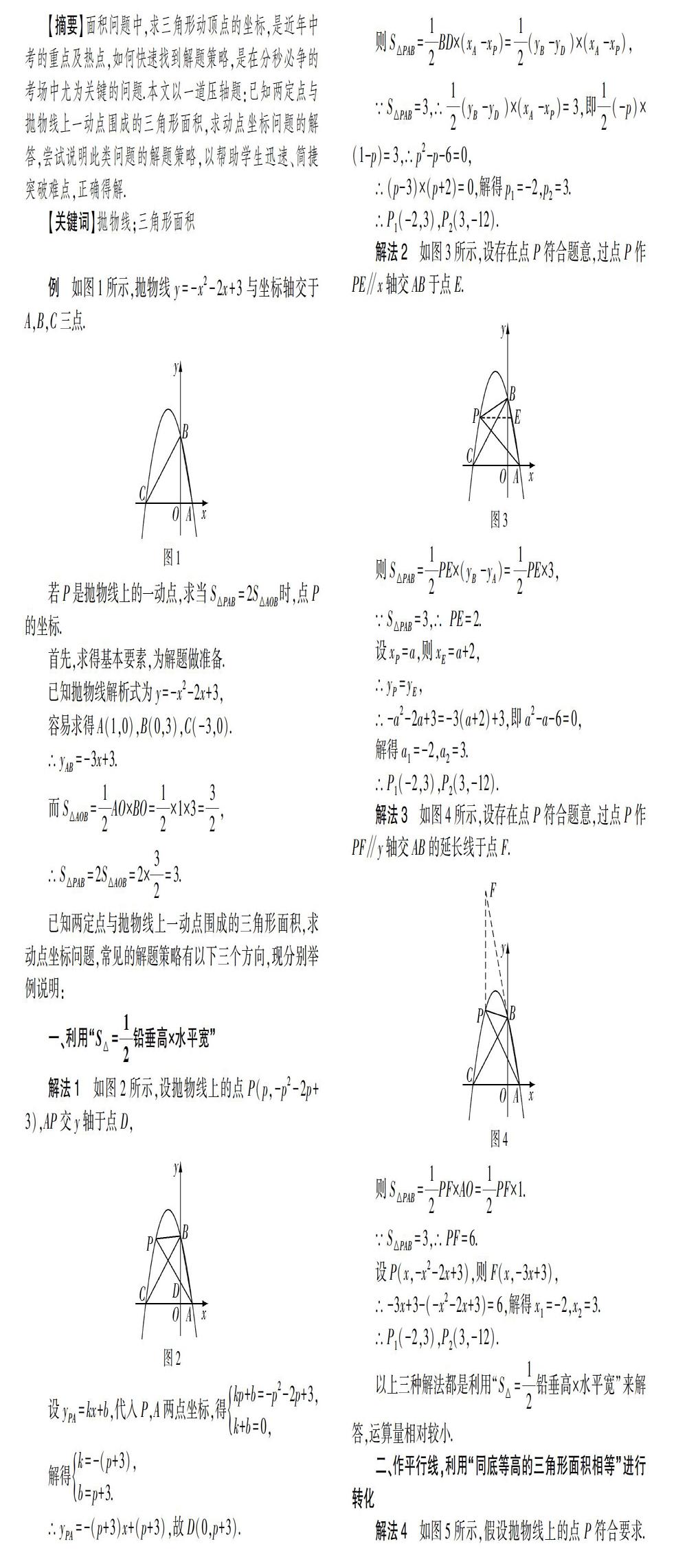
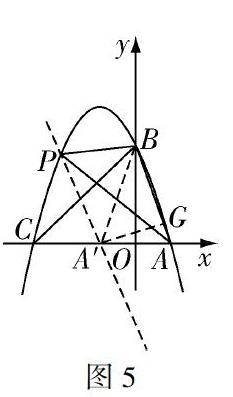
【摘要】面积问题中,求三角形动顶点的坐标,是近年中考的重点及热点,如何快速找到解题策略,是在分秒必争的考场中尤为关键的问题.本文以一道压轴题:已知两定点与抛物线上一动点围成的三角形面积,求动点坐标问题的解答,尝试说明此类问题的解题策略,以帮助学生迅速、简捷突破难点,正確得解.
【关键词】抛物线;三角形面积
参考答案 (1)抛物线的解析式为y=-x2-2x+3.
(2)存在满足条件的点P,其坐标为(-1,5-1)或(-1,-5-1).
(3)点F的坐标为1-37[]2,337-15[]2.
