把握高考方向，精准定位教学

胡琨

【摘要】本文记述了“正态分布”复习课的教学过程，先通过课前练习完成基础知识储备目标，再利用题组训练强化学生对利用正态密度曲线图像的对称性解决实际问题的通法通解的理解，最后带领学生感受高考真题.通过小组合作探究，请学生代表发言，让学生们从题目中读取有用数据，分析实验特征，辨识模型，解决实际问题.同时总结了高中阶段三个随机变量模型的特点和区别.全篇以“把握高考方向，精准定位教学”为目标，以学生为主体，以思维为核心，全面提升学生的数学核心素养.

【关键词】正态分布;密度曲线;对称性;教学实录;精准定位;小组成果展示

一、基本情况

1.教材分析：本节内容是江苏新高考中增加的考点，以客观题为主.学生需要了解正态分布密度曲线的特点及其表示的含义，利用正态分布解决实际问题.

2.授课对象：四星级高中文科班的学生，基础较好，发言积极，有一定的逻辑能力、运算能力和总结表达能力.

3.教学目标：

（1）通过误差模型，了解服从正态分布的随机变量.通过实例，借助频率分布直方图，直观地了解正态分布的特征.

（2）了解正态分布的均值、方差及其含义.

二、教学过程

今天我们来复习正态分布.

先回顾一下正态密度曲线的生成过程.

画出数据的频率分布直方图，连接频率分布直方图中各小长方形上端中点，得到频率分布折线图.当研究总体的数据无限增多，且组距无限缩小时，频率分布折线图无限接近于一条光滑的曲线，生成概率密度曲线.我们发现该密度曲线在均值附近的值较多，远离均值的值较少.我们把具有这种特性的曲线叫正态密度曲线.

师：通过课前的四个练习题，同学们一起复习了正态分布的概念、参数表示的意义、正态密度曲线的特征与性质以及3σ原则，完成了本堂复习课最基础的知识储备目标.

通过本道高考真题，教师把课堂交给学生，同时提升学生对应用题的理解和认识，引導学生利用公式和图像提取有用数据，分析实验特征，辨识模型，先确定随机变量满足何种分布，再进行解题.

三、教学回顾与反思

1.把握高考方向.

（1）正态分布是高中阶段唯一用来刻画连续型随机变量的模型

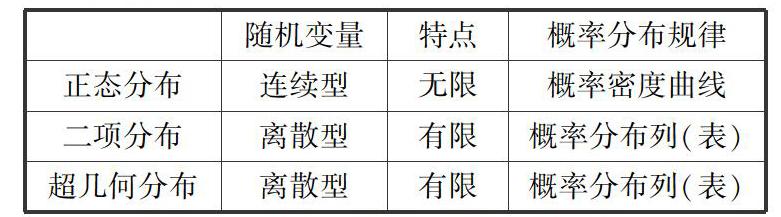
按照当前课程标准“主线—主题—核心内容”的基本结构，我们可以把随机变量分为离散型随机变量和连续型随机变量.离散型随机变量的刻画模型主要有二项分布、超几何分布等，而连续型随机变量的刻画模型高中阶段只介绍正态分布.

（2）3σ原则可以用来作出科学的决策

3σ原则有着重要的实际意义.依据小概率事件在一次试验中几乎不可能发生的特点，对事先所作的统计假设作出判断：是拒绝假设，还是接受假设.

同时应注意两点：一是“几乎不可能发生”是针对“一次试验”来说的;二是当我们根据“小概率事件几乎不可能发生”进行推断时，也有3%犯错的可能性.

（3）正态分布在生活中的重要作用与实际意义

从概率分布的角度，生活中一些随机变量虽然不服从正态分布，但其中必有x%（x≤100）是服从正态分布的.有些离散型随机变量的分布的极限就是正态分布，正态分布又可以用公式转化为标准正态分布.因此正态分布是数据科学和机器学习领域内的核心.

2.精准定位课堂教学.

正态分布为江苏高考的新增考点.本节复习课的教学目标圆满完成，教师通过题组训练，让学生了解正态密度曲线的特征，了解正态分布的均值、方差及其含义，引导学生利用文字和图像读取有用数据，分析实验特征，辨识模型，确定随机变量满足何种分布，进一步解决实际问题，同时培养了学生数据分析、数学建模、数学运算等数学核心素养.

3.合作交流与对话展示.

“合作交流”指在教学过程中，学生在小组内互动合作，提出有价值的问题，并到讲台前展示小组成果，同时也将小组内不能解决的问题在全班范围交流.老师通过与学生的对话，启发学生思维，把课堂交给学生，教与学的过程充满成长的气息.

【参考文献】

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018.