基于静力响应信号的变截面梁损伤识别

李继伟 汪 城 罗 帅

(1.绍兴文理学院 土木工程学院, 浙江 绍兴 312000;2.广州城市职业学院, 广东 广州 510405)

0 引言

工程实践中广泛应用变截面梁[1-2]，例如，大跨度预应力混凝土连续梁桥以及钢构桥等常用的桥梁结构形式，为了使结构内力变化更加合理，一般将支座附近的梁高加大，而跨中附近的梁高取得较小，从而形成变高度梁[3-5].这些变截面梁结构在服役期间，由于诸如外物碰撞、疲劳积累和环境腐蚀等因素的影响，将不断积累损伤[6-10].结构某部分的损伤可能会导致结构整体迅速破坏，并由此造成严重后果.因而，对结构损伤的早期预测显得尤为重要.传统的检测损伤的方法是可视化或局部化的实验方法，如超声或超声波方法、磁场方法、雷达成像和涡流及温度场等方法.但这些方法只能检测结构表面及附近的损伤，且工作量大、耗费高[11-12]，导致基于结构静动力响应的损伤识别方法迅速发展.

近几十年来，在变截面梁损伤识别方法的研究方面，许多学者进行了有益的工作，提出许多方法.冯侃[13]等提出基于振动的变刚度复杂梁结构的损伤检测方法.徐勇华[14]等提出基于挠度影响线的变截面梁损伤识别探究.周俐俐[15]等利用曲率模态和柔度曲率对变截面钢梁进行多损伤静态识别.黄健[16]等探究了离散小波变换在变截面梁损伤识别中的研究应用.小波变换和曲率模态对于解决一些动力响应的问题具有识别精度高的优点，但对于静力响应问题还没有较为简单准确的方法解决.为了解决这个问题，本文引入基于结构刚度灵敏度的损伤识别方法，可以根据损伤因子的降低导致刚度矩阵的变化来识别结构或构件的损伤情况，以一个变截面简支梁结构为例验证该方法.结果表明, 本文方法是可行的.

1 变截面梁的单元刚度矩阵

对于高度线性变化的变截面梁单元，如图1所示，假设其长度为L，宽度为b，大截面梁高为h，小截面梁高为k·h，弹性模量为E.

图1 高度线性变化的变截面梁单元纵面

根据有限单元法基本原理可以得到变截面梁的单元刚度矩阵[2]为：

(1)

依据拼接的方法，将图1所示的变截面梁单元等效为高度为h的矩形截面时，可以得到含截面惯性矩I的高度线性变化的变截面梁的单元刚度矩阵ke为：

(2)

从式(2)中可以看出能引起变截面梁的单元刚度矩阵发生变化的主要是因为惯性矩的降低，从而导致变截面梁结构发生损伤破坏，所以这里可以称惯性矩I为损伤因子.

2 利用能量原理建立整体刚度矩阵

对于含有n个结点的变截面梁结构，每个结点有2个自由度(这里忽略轴向变形)，因此结构的整体刚度矩阵为2×n阶，其整体结构的位移向量U可以表示为：

U=[V1θ1…Viθi…Vnθn]T

(3)

式(3)中的V和θ分别表示变截面梁结构在静力荷载作用下的竖向位移和弯曲变形量，下标表示单元节点编号，上标T表示为矩阵的转置(下同).在整体结构的位移向量中提取对应的单元位移分量d，即：

(4)

式(4)中S为提取矩阵，其表达式为：

(5)

式(5)中下标为元素所在的行与列，省略部分均为零元素.

对于变截面梁单元i，其弹性应变能(标量形式)在局部坐标下写成内积的形式为：

(6)

将式(4)代入式(6)中可得变截面梁单元i在整体坐标下的弹性应变能Pi为：

(7)

根据能量守恒得到变截面梁结构在整体坐标下的弹性应变能P为：

(8)

综合式(7)和式(8)可以得到集成后的变截面梁结构的整体刚度矩阵K为：

(9)

3 利用损伤因子的变化量对结构进行损伤识别

由结构的静力平衡方程有：

K·U=F

(10)

式(10)中的F表示为变截面梁结构所承受的结点力向量；综合式(2)，式(5)和式(9)可知，结构静力平衡方程中含有各个单元的截面惯性矩Ii(损伤因子)，于是对式(10)左右两边分别对其求导可得：

(11)

由式(11)整理得到变截面梁单元i的灵敏度矩阵为：

(12)

将式(12)累加得到：

(13)

当结构构件发生损伤后，结构的静力平衡方程为：

(K-ΔK)·(U+ΔU)=F

(14)

式(14)中的ΔK为结构整体刚度矩阵总的损失量，其表达式为：

(15)

式(15)中的ΔIi表示当结构各构件发生损伤时，相应的各构件的损伤因子的损失量，所以其表达式为：

ΔIi=Ii·αi

(16)

式(16)中的αi为各单元i的损伤系数，综合式(10)和式(14)可以得到结构位移向量的增量ΔU为：

ΔU=(K-ΔK)-1·F-K-1·F

(17)

又由Taylor级数展开的矩阵形式表达有：

(18)

取式(18)中的一阶线性部分得到：

(19)

将式(13)代入式(19)中得到：

(20)

将式(20)写成向量形式可以表示为：

(21)

考虑实际情况下，损伤因子即结构构件的截面惯性矩不可能为负值，所以结构损伤后其变化量ΔIj也不会为负值；于是由式(21)可以得到：

(22)

将式(17)代入式(22)中得到：

{(K-ΔK)-1·F-K-1·F}

(23)

综合式(16)和式(23)，利用最小二乘法，最终可以得到各单元的损伤系数.

4 算例

以图2所示的变截面简支梁结构为例，验证本文所提的损伤识别方法.该结构的基本参数为：弹性模量E=2.0×105MPa，跨度L=10 m，宽度b=10 m，跨中高度h0=0.1 m，支座处梁高h1=1.0 m.可能的静力加载点也见图2中.考虑三种加载方式，方式1：F1=10 kN,F2=0,F3=0;方式2：F1=10 kN,F2=10 kN,F3=0; 方式3：

F1=10 kN,F2=10 kN,F3=10 kN.显然，这3种加载方式是线性无关的.讨论3种损伤情况，列于表1中.

表1 变截面简支梁结构3种损伤情况

损伤情况1损伤情况2损伤情况单元编号损伤程度(%) 单元编号损伤程度(%) 单元编号损伤程度(%)1410 25 2301010 10351815 1840

图2 变截面简支梁结构及其静力加载

对于第一种单个单元损伤情况，三种加载方式下识别出的结果是完全相同的(这是由于我们设定的加载方式所造成的损伤情况是相同的).其结果为：单元14发生损伤且其损伤程度计算值α14=11%，其余各单元的损伤程度计算值均为0，所以本文所叙述的方法对于在静力加载下，能够十分精确地对变截面梁结构进行损伤定位.

对于第二种多单元小损伤情况，不考虑测量误差时三种加载方式下所得到的各单元损伤程度如图3所示，其中单元2、单元10和单元18损伤程度计算值为α2=5%，α10=11%，α18=18%，和设定值基本一致.

由图2和图3可见，本文所叙述的方法不仅能十分精确地对变截面梁结构进行损伤定位，还可以对于一些能感觉到甚至肉眼无法发现的较小程度的损伤结构或构件的损伤程度进行比较准确的识别.对于第三种多单元大损伤情况，不考虑测量误差时三种加载方式下所得到的各单元损伤程度如图4所示，其中单元2、单元10和单元18损伤程度计算值为α2=43%，α10=54%，α18=67%和设定值相差比较大.

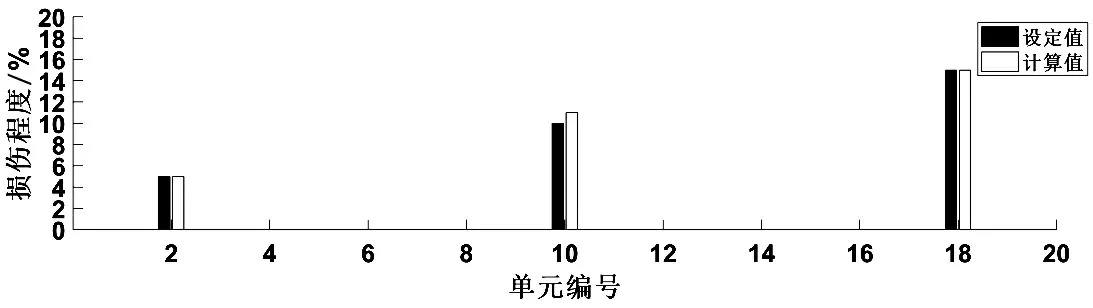
图3 单元2、单元10和单元18刚度损伤5%、10%和15%时的识别结果

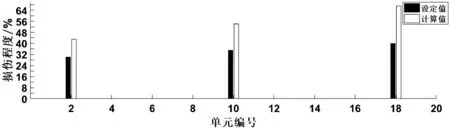
图4 单元2、单元10和单元18刚度损伤30%、35%和40%时的识别结果

由图4可见，本文所叙述的识别方法对于损伤程度比较大的结构或构件，计算得到的损伤系数与设定的损伤系数比较发现这种只考虑一阶灵敏度矩阵的损伤识别方法，其识别的精度还有待进一步提高.

5 结论

本文利用对结构静力平衡方程的损伤因子求导推导了单元刚度的灵敏度矩阵公式，依此建立了基于刚度灵敏度矩阵的结构损伤识别方法.算例结果验证了所提方法的可行性.本文方法计算简单，易于计算机编程而且对连续材料均适用，桥梁结构中的变截面梁通常为高强混凝土且工作在弹性阶段，因此本方法对小损伤情况是适用的，但对于结构发生大损伤的情况则存在着识别结果误差较大的缺点，但考虑到工程实践中结构在保证安全适用的原则下可容许发生损伤的范围较小，所以本文方法仍具有较广的应用空间.