基于遗传算法的光传送网络规划

刘小钰，李士心，张 海

（天津职业技术师范大学电子工程学院，天津 300222）

光传送网络（optical transport network，OTN）可以在光域中实现业务信号的传输、复用、路由和监控，且性能和生存能力仍可以得到保障[1-2]。在确定城市连接数和资源限制的情况下，如何连接足够多的区域则是迫切需要研究的课题，这是一种组合寻优的问题，容易描述但难于处理。本文通过对全国12 个城市群间所构筑的传送网络连接与网络价值进行建模仿真与分析，寻找出网络价值最大化的连接方式。

1 光传送网络的网络价值及模型数据的选取

1.1 光传送网络的网络价值

不同传输格式下的传输距离如表1 所示。3 种典型光传输设备参数在优化升级后均发生了变化。

表1 不同传输格式下的传输距离

优化通信网络的目的是在资源一定的情况下，把更多的人口更充分地连接到一起，网络价值定义如下。

（1）给出连接的定义 直接连接2 个区域的链路。

（2）根据要求给出单个连接的价值定义 连接区域人口数乘积的开方与传输容量的乘积。

网络的价值则是所有连接价值的加权和，即

网络价值=∑权重×容量×人口

下面举例说明网络价值的计算方法。选取北京、上海、南京3 座城市，3 个节点网络示意图如图1 所示。

图1 3 个节点网络示意图

首先要求3 座城市之间互有连接，然后根据城市之间的距离可以得到传输容量，进而由传输容量配合人口数算出网络价值（network value，NV）为（假定每条传输链路的权重为1）

式中：m 为百万人（million）。

该网络的连接数为3，但是现实生产中，不可能让每2 个城市之间均互有连接，这样对资源是极大的浪费。实际上要想将这3 个地区的人口实现互联，并不需两两城市之间建立连接，可通过使用中间转节点的方式连接起来[3]。从如图1（b）可知，北京和南京之间需通过上海中转，这种情况下只需要建立2 个连接，即北京-上海，上海-南京。可进行如下安排：先保留一半容量（100 GB/s）给北京-上海之间的传输，而剩下的另一半容量用于南京-北京的信号传输（100 GB/s），同时南京-上海之间的直接传输容量也会降低至300 GB/s，此时网络的价值[4]为

根据需要2 个节点之间也可以有多个连接。

1.2 模型数据的选取

在全国范围内选取典型的12 个城市构筑一个城市群，包括哈尔滨、北京&天津、上海、郑州、武汉、西安、重庆、成都、拉萨、乌鲁木齐、广州&深圳、昆明。

（1）由表1 及城市间距构建传输总容量，为了直观显示，还需将各城市的坐标位置（经度和纬度）显示在图上[5]。

（2）由传输连接数的要求计算出总容量，而后由总容量及城市人口数建立起网络价值的函数，本研究所使用的人口数为各城市在某年的人口数据统计。共有12 个城市，故要实现两两互联总连接数需有（12×11）/2=66 条。可知当连接数为66 条（即每2 个城市之间均互有连接）时，网络总价值以及传输总容量是一个确定的算术问题，不需要借助该算法来寻优，且此时的网络价值最大，资源耗费也最大；而此处需要权衡连接数与网络价值的关系，基于资源等因素的限制，本研究只求解连接数为33 条、17 条以及49 条时的总容量以及网络价值来进行对比，以分析在限定连接数即限定资源配置的情况下，如何连接更多人口，达到网络价值最大化[6]；也可分析如何平衡东西部的连接。

2 遗传算法机理及优化模型建立

2.1 遗传算法机理

在遗传算法中，对于要优化解决的问题可将其编码为一个简单的字符串，将其称为染色体[7]。本研究中采用实数编码，将2 个城市之间的连接进行编码且不用解码，这样既符合合理化需要又能简化程序。在算法的开端先随机生成1 个种群（即1 个染色体群组）。对于每个个体计算其适应度值并排序，然后进行选择、交叉、变异等一系列遗传操作，再根据适应度来排序，选择出新的种群，周而复始，直到终止条件出现[8]。

2.2 遗传算法实现以及优化模型建立

（1）种群初始化。应用实数编码进行染色体的编码，个体包含了城市群及两两互联时所需连接数，由于共有12 个城市，要实现两两互联可知总连接数有（12×11）/2=66 条；由此可知每个个体编码长度为66，另外根据算法要求和实验效果可设置种群规模为100，进化次数为600。

（2）适应度函数。由于此发明是在给定区域连接数的情况下去求解网络价值最大化的连接方式，故适应度函数采用整个光传送网络的网络价值来表示。

（3）遗传操作—选择。采用“轮盘赌”选择法从第t代群体中选择出一些适应度值高的优秀个体遗传到下一代群体中[9]。该方法简单实用又不失精确性。这种选择基于比例来进行：若个体i 个适应度为fi，种群大小为NP，则个体i 被选择的概率为

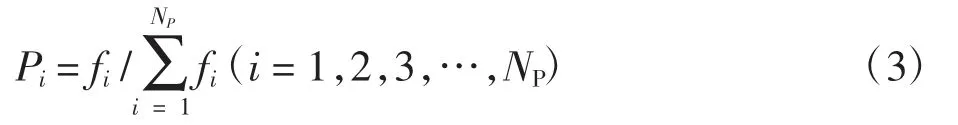
（4）遗传操作—交叉。交叉是指将个体进行两两配对并交换部分染色体片段，其作用较为关键，可以使得优秀个体的优秀基因传递到下一代。采用“君主方案”进行交叉操作，首先选择适应度值最高的染色体作为君主染色体，放在整个种群的奇数位，与其靠后一位的偶数位构成一对，接着根据交叉概率Pc确定交叉点的个数（Pc= 0.8），确定规则为：n = round（D × Pc），其中D 为染色体的维数，然后按交叉点个数，根据随机生成的交叉位将每对染色体进行交换片段，得到新种群[10-11]。

（5）遗传操作—变异。变异保证了种群基因的多样性，变异概率此处不应太大，可设Pm=0.2，否则基因突变的可能性较大。从交叉后得到的种群中按变异概率Pm随机选一些进行变异的个体，确定变异位后将该位的二进制取反，生成一个新个体。

对新产生的群体返回第（2）步，再进行一轮运算，对个体适应度值再进行优化，多次循环，直至终止循环的条件出现[12]。

3 模型训练及仿真结果分析

对于整个城市群的传输链路而言，先将各城市坐标显示在图上，连接数为33、17、49 条时的最大传输容量、连接情况及网络价值分别如图2、图3 和图4 所示。

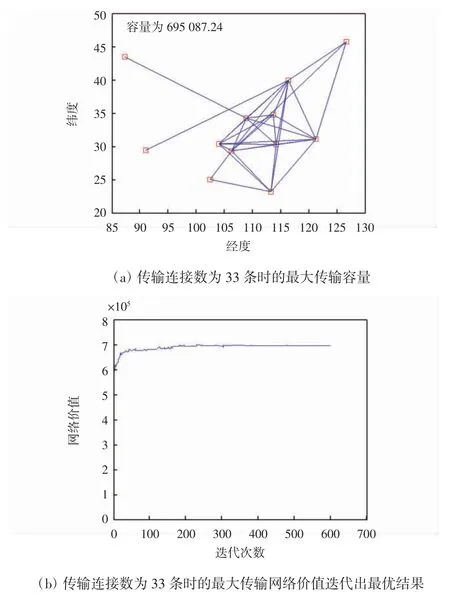
图2 连接数为33 条时的最大传输容量、连接情况及网络价值

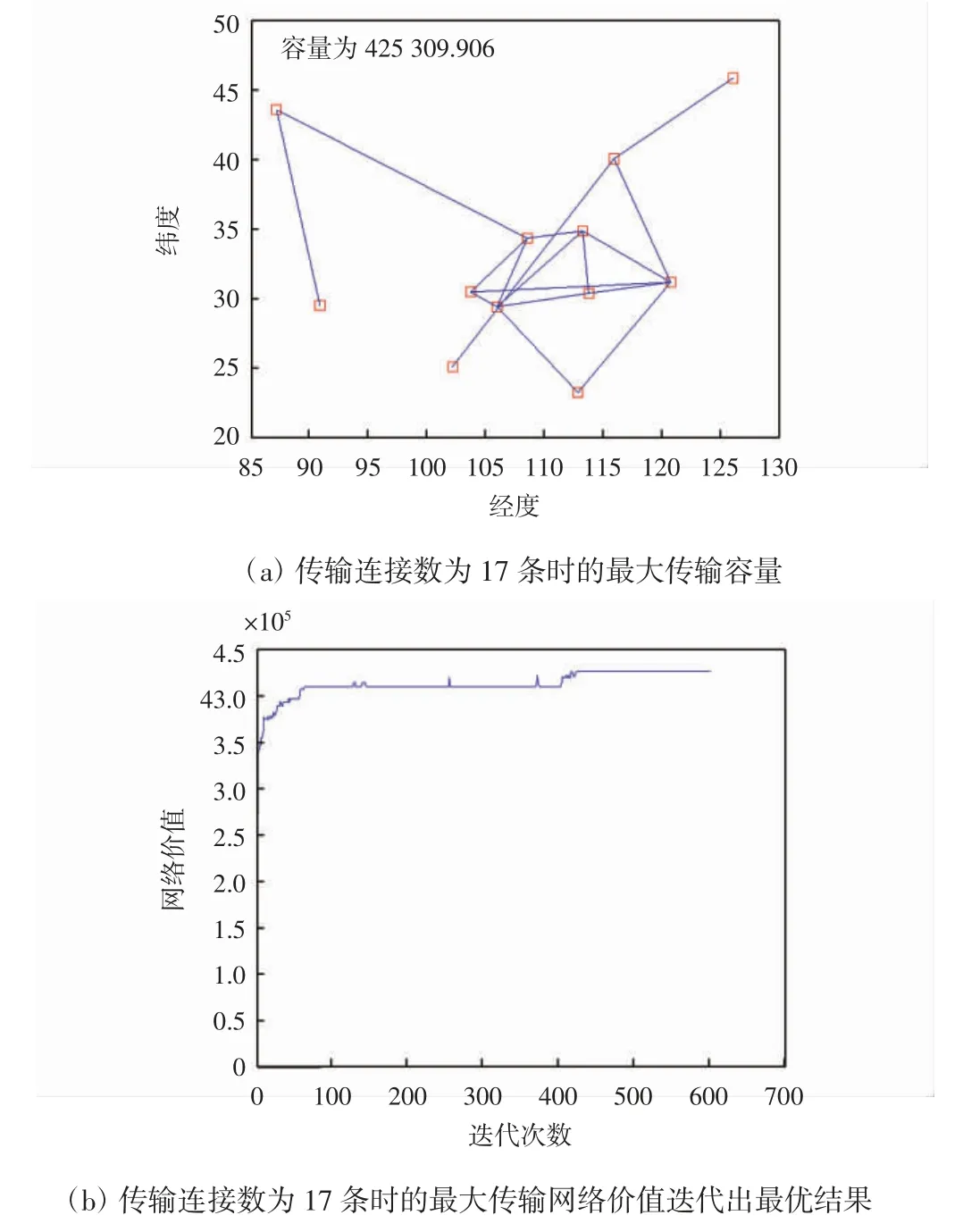
图3 连接数为17 条时的最大传输容量、连接情况及网络价值

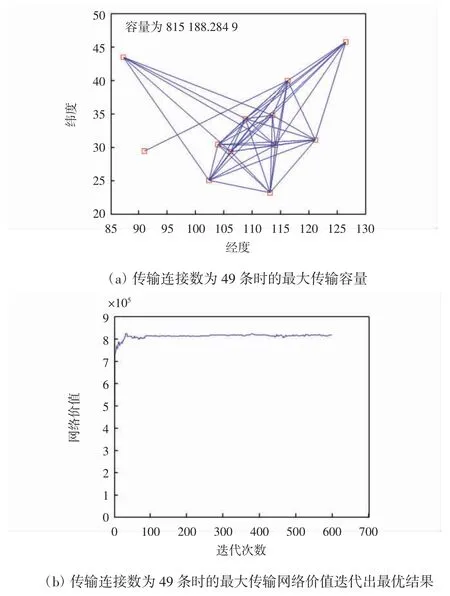
图4 连接数为49 条时的最大传输容量、连接情况及网络价值

图2（b）、图3（b）、图4（b）为最大传输网络价值迭代出最优结果的过程，由图可知，随着迭代次数的递增，网络价值逐渐增大最后趋于稳定。这3 次迭代所选择的连接数是总连接数的三等划分点，由实验结果可得：连接条数在17 及以下，虽连接条数精简了，资源也节省了，但传输容量以及网络价值太小，这样的网络连接不利于生产生活；连接条数在49 条及以上时，传输容量和网络价值均达到了很高的值，极大便利了区域间的信息互通，但与此同时带来的损耗却是连接数和资源配置的增加，这种连接情况适用于发达国家或区域的配置。而对于发展中国家或地区，联通一片区域，既要考虑实现互联互通的最大化，也要考虑经济基础和资源配置损耗，因此33 条连接较为合适[13-15]。

4 结 语

遗传算法相对于一些传统的寻优方法收敛性有所增强，耗时少，精度高。本研究在城市群之间建立连接的过程中，可通过遗传算法逐步迭代寻得最优的连接方式以及最大的网络价值和传输总容量，这时便可在传输容量一定的情况下，根据优化结果减少不必要的连接，精简资源配置。本研究也可修改网络价值的权重，有针对性地使传输连接偏向某一地区，更有利于合理规划统筹。