一类分数阶超混沌系统的有限时间控制
2020-03-24赵小山
徐 涛,赵小山,卢 雅
(天津职业技术师范大学理学院,天津 300222)
在过去的几十年中,越来越多的数学和物理领域的研究者们对分数阶微积分产生了浓厚的兴趣[1]。一方面,分数阶微积分可以将微分和积分推广到任意阶数并且分数阶微积分可以更加准确地模拟出许多动力系统的动力学现象,如机械系统[2]、流体力学系统和生物工程[3]等。另一方面,运用分数阶微积分的定义可以更加方便地设计鲁棒控制器,因此分数阶微积分常用于混沌控制领域[4]。
随着进一步的研究,将分数阶微积分运用在混沌控制中已经成为数学和物理领域里面的一个热点研究课题。许多的控制方法相继提出,如自适应控制、追踪控制[5]、脉冲控制[6]和模糊滑模控制[7]等,然而这些控制方法不能确定当系统达到稳定时的时间,所以在20世纪60年代初期Dorato 为了能够控制系统在有限时间内达到稳定,提出了整数阶有限时间稳定性,并于2003年Hu 等[8]通过对分数阶混沌系统研究,成功实现分数阶Lorenz 混沌系统的有限时间稳定,进而提出了分数阶有限时间控制方法。但前者所使用的模型为经典的分数阶混沌模型,对其他较为复杂的分数阶超混沌模型的研究较少。本文通过运用分数阶有限时间控制方法,针对一个新的分数阶超混沌模型进行有限时间控制研究,利用数值仿真描述了该系统的动力学现象,并通过定理设计出该系统的控制器,最终通过数值模拟实验验证了其有效性。
1 分数阶系统模型
1.1 分数阶微分概述及定义
在现今分数阶微积分研究过程中,微分和积分主要分为 3 种定义,分别为 Riemann-Liouville(R-L)定义[9]、Grunwald-Letnikov(G-L)定义[10]以及 Caputo 定义[11]。在阶数为负实数和正整数时,3 种分数阶微积分的定义相同,但在其他情况下,R-L 定义与Caputo 定义相较于G-L 定义适用面更大,所以R-L 定义与Caputo 定义较为常用,其中R-L 定义更多地用于纯数学领域的研究,Caputo 定义更适用于工程领域的研究,本文采用的是Caputo 定义。
定义1Caputo 分数阶微分定义[12]。
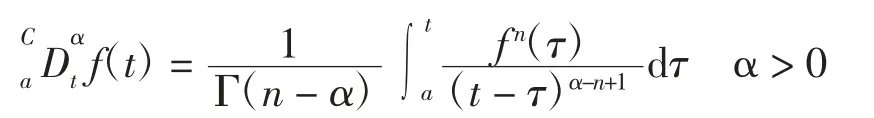
式中:C 为 Caputo 微分;α 为阶数;n 为整数,且满足n-1 < α < n;a 和 t 分别为运算的上、下线;Γ(·)为Gamma函数。
定义 2Gamma 函数定义[13]。

引理 1[14]假设 x(t)∈Rn是连续的可微函数,P∈Rn×n是一个正定矩阵,那么对于 α∈(0,1),满足不等式

特别地,当 x(t)∈R 是一个连续可微函数时,可以得到

引理 2[15]假设 xi=x1,x2,…,xn为实数,且 0 < q≤2,则下列不等式成立。

引理 3[16]假设 V(t,x(t))是一个 Lyapunov 函数,m、n 为任意正数,且存在一个类α 函数αi(i=1,2,3)满足下列不等式,则说明该系统满足全局Mittag-Leffler 稳定。
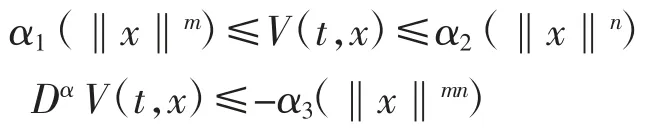
1.2 分数阶超混沌系统模型

式中:xi为状态变量,i= 1,2,3,4;βi为系统参数,i=1,2,3,4;ui为该系统的控制器,i=1,2,3,4。
健康雄性Wistar大鼠100只,体质量180~220g,由济南朋悦实验动物繁殖有限公司提供,实验动物生产许可证号SCXK(鲁)2016‐0007 。
分数阶超混沌系统的相轨迹如图1 所示,时间历程如图2 所示。
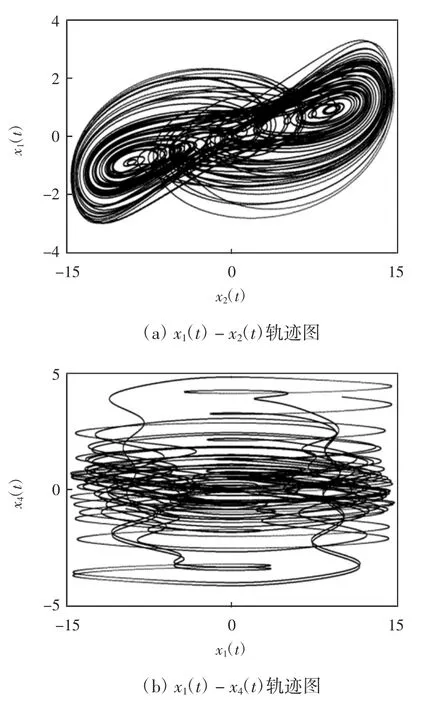
图1 分数阶超混沌系统的相轨迹
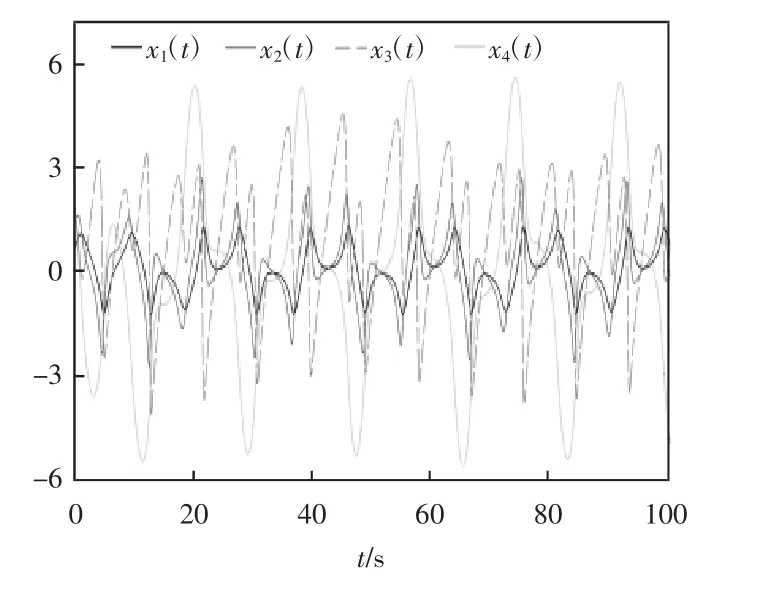
图2 时间历程
2 有限时间控制
2.1 有限时间控制稳定性定理
在数学与物理领域对分数阶混沌系统的控制研究已成为当下最热门的研究之一,成功吸引了人们的关注,其中在多种控制方法里面,有限时间控制的强鲁棒性,收敛速度快,在有限时间内稳定等特点被人们所接受。本文正是通过运用有限时间控制[17]的方法对该分数阶超混沌系统进行控制研究。
定理1一个任意的分数阶混沌系统满足全局Mittag-Leffler 稳定[18]即满足引理 3 且满足 DαV(t,x)≤则说这个分数阶混沌系统是有限时间内稳定的,安定时间T 为
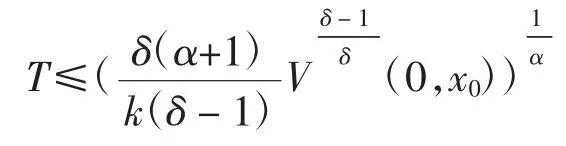
2.2 有限时间稳定性的证明
通过定理 1 得到该系统控制器 ui=u1,u2,u3,u4为
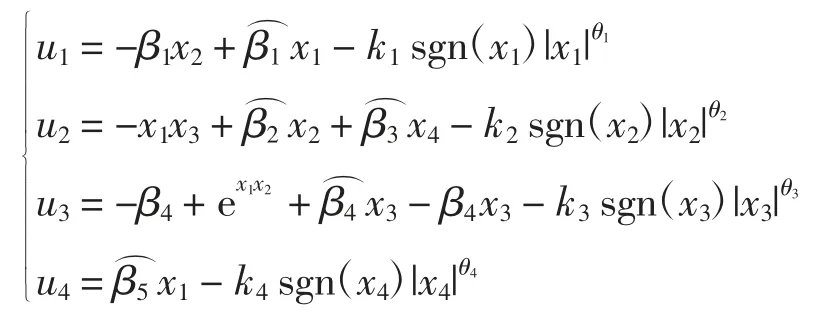
存在一个Lyapunov 函数[19]

根据引理 1 和式(2)可得
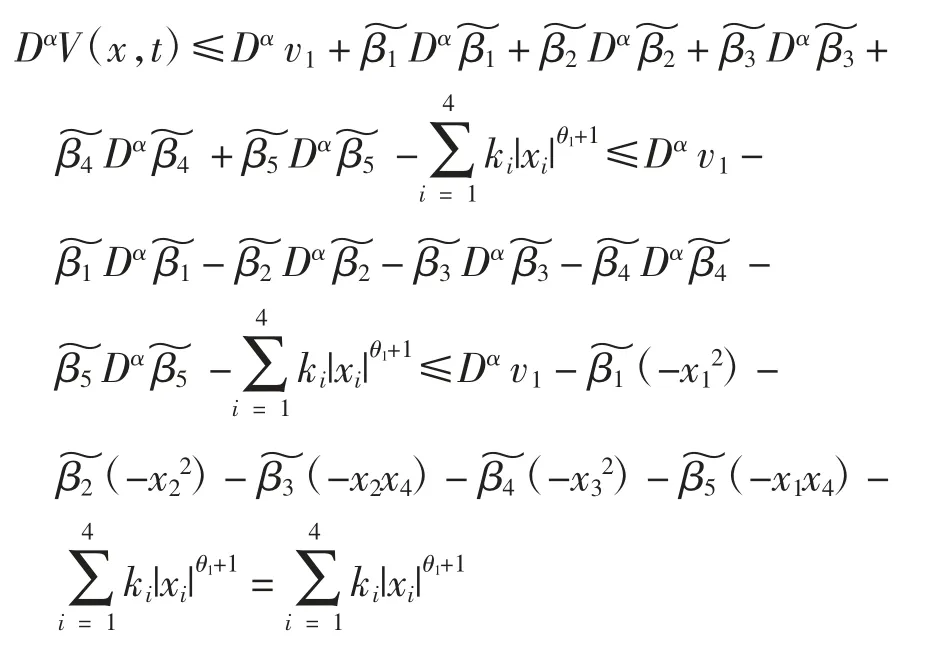
式中 ki恒大于 0,i=1,2,3,4,故 DαV(x,t)< 0,且当 DαV(x,t)<0,必定存在一个 α3函数使得 DαV(x,t)≤-α3‖x‖2,则该系统满足全局 Mittag-Leffler 稳定。

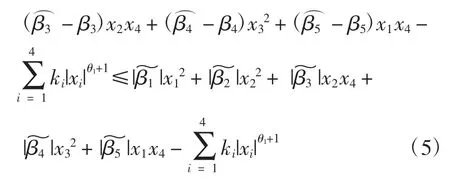
根据引理 2 和式(5)可得



根据定理1 中Dαv1是有限时间稳定的,因为DαV(x,t)是全局 Mittag-Leffler 稳定且 Dαv1中所有初值包含在 DαV(x,t)里,所以 DαV(x,t)是有限时间稳定的。
3 数值仿真
采用Matlab 进行数值仿真,步长Δt=0.005,仿真时间T=2 s,阶次α=0.98,相关参数取值为β1=0.87,β2=0.5,β3=0.37,β4=2.5,β5=0.5。
该系统的初值为x1(0)=2,x2(0)=1,x3(0)=-1,x4(0)=-2。根据定理可得T≤1.83 s,控制效果图如图3 所示。
由图3 知,该分数阶超混沌系统达到稳定的时间约为1.5 s。在所计算出的稳定时间T 之内,证明了该控制器的有效性,且从图像的走势可以看出其收敛速度之快,同时证明了有限时间控制方法的强收敛性。

图3 控制效果图
4 结 语
本文研究了一类分数阶超混沌系统的有限时间稳定性定理,并通过该定理设计出了符合该系统的控制器,最终对参数以及变量赋值,实现了分数阶超混沌系统达到解的稳定并计算出了达到稳定的有限时间数值,通过数值仿真验证了结论的可行性及该控制方法的强收敛性、鲁棒性。该控制方法可进一步改进,针对不同的分数阶微积分定义设计不同的控制器,并在噪声或时滞干扰下,其控制效果的变化也需进一步研究。
