一类特殊曲线上Cauchy积分在尖点处奇异性分析

贾 婕，刘 华，边小丽

（天津职业技术师范大学理学院，天津 300222）

解析函数边值问题（或Riemann-Hilbert 问题）[1]是复分析领域的经典问题，它不仅在很多理论数学分支有重要应用，同时在平面弹性断裂力学、空气动力学、散射理论等应用领域也不可或缺。国外一些学者在这方面做出了杰出的工作，其中Muskhelishvili[2]奠定了解析函数边值问题的理论基石，其著作《奇异积分方程》为弹性学的应用带来助力；国内也有不少学者从事这方面的研究，特别以路见可教授[1]的《解析函数边值问题》为代表，该书系统地论述了解析函数的各种基本边值问题及其在奇异积分方程上的应用[3]，包括Riemann 边值、Hilbert 边值、复合边值等问题。在此基础之上，后继的学者们对一般Riemann 边值问题也进行了推广，取得了更多关于边值问题的相关成果[4-9]，得到了复合边值问题在不同情况下的一般解。

近年来，对于解析函数边值问题及奇异性的经典研究多以简单封闭曲线和开口曲线为主，研究多种材料复合的弹性断裂问题中[10]，可能涉及多条交叉曲线上的边值问题。曲线交叉一般可分为横截相交和相切相交。对于逆散射问题、随机矩阵等领域[11-13]，更广泛应用到非横截相交曲线上的解析函数边值问题。相对于横截相交曲线上边值问题研究的丰富成果，相切相交的曲线（即非横截相交曲线）由于切点处（节点处）的奇异性问题并没有得到充分研究，同时Fokas 等[14]利用R-H 技术研究可积系统，也引出了带节点的边值问题的研究。为此，本文讨论相切相交产生节点的特殊曲线上的相应问题，研究Cauchy 积分在2 种不同条件下处理对应尖点处的奇异性，为解决非横截相交曲线上的解析函数边值问题等提供条件。

1 Riemann边值问题的描述

含节点特殊交叠曲线图如图1 所示。

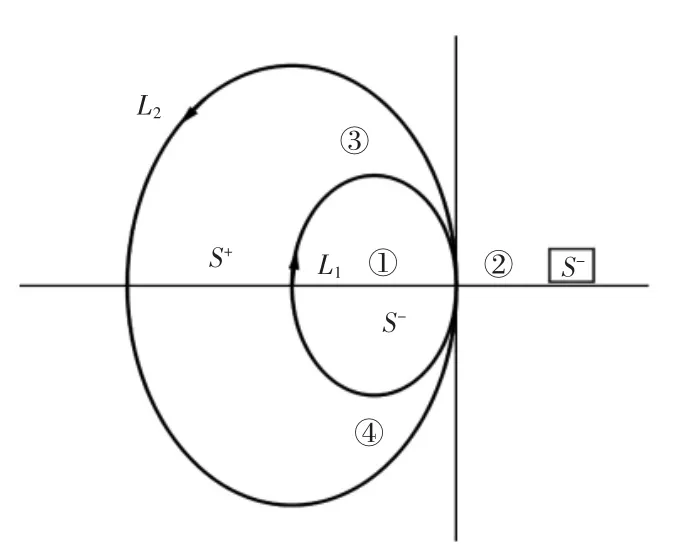
图1 含节点特殊交叠曲线图

设L 为复平面上2 条光滑封闭的相切Jordan 曲线L1和L2（即L=L1+L2），曲线相切产生的节点位于原点。L1取顺时针为正向，L2取逆时针为正向。此处假定L 把整个平面分成4 组区域：①、②区域合并为S-，③、④区域所在的近似圆环的内域为S+（包含2 条曲线的边界点）。从图1 可知，S 并不连通。

Riemann 边值问题（简记为R 问题）即：求以 L为跳跃（间断）曲线的一个分区全纯函数Φ（z），满足边值条件

式中：G（t）、g（t）在 L 上均满足 H 条件。

如果要求Φ（z）在∞处至多为m 阶，则此问题将记为Rm[1]。一般最常讨论的是问题R0和R-1，前者要求Φ（∞）有限，后者要求 Φ（∞）=0。

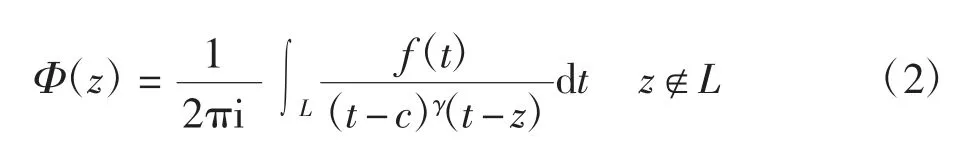
式中：f（t）在 L 上为 H 函数，且 0 ＜ Reγ ＜ 1。

2 给定不同区域中节点奇异性讨论

讨论给定问题中4 个不同区域趋向于节点时节点附近的性质，主要考虑以节点为端点时不同的曲线方向的叠加对其端点奇异性的影响。

2.1 割破封闭曲线转换问题

先假定L 为一条封闭光滑曲线构成的情况，并取定图1 中L1和L2的方向。考虑对于节点问题的处理，需要在原曲线上取一条主值分支将原曲线被一条由零点到负无穷远处的线切割成 l1、l2、l3、l44 条曲线，分割后的曲线方向图如图2 所示，曲线方向保留原方向，即为曲线节点。这样就将问题转化为4 条开口曲线交于一点的R 问题，解决了封闭曲线无法定义log 函数的障碍。

图2 分割后的曲线方向图

给定 f（t）在每一条 Lj上都属于H。当t 沿某一Lj趋向于c 点时，f（t）有确定的极限值fj（c）。若以fj（c）作为f（t）在lj上c 处的值时，fj（c）在Lj上属于H，即f（t）在整个 L 上属于 H。

此时需先考虑Cauchy 积分性质。对每一条Lj，当t∈Lj时，若把平面沿Lj剖开（延伸到无穷远处剖开），它就是（z-c）γ在z=c 附近的一全纯分支[（z-c）γ]j在lj正侧的边值，简记为[（t-c）γ]j。

参照文献[1]，对于Cauchy 型积分

式中：γ = α +iβ≠0，0≤α＜ 1，c=a 或 b；f（t）∈H，且 L取定自 a 到 b 的方向为正向。（t-c）γ理解为从 c 沿 L伸向无穷远剖开的平面上（z-c）γ的一个全纯分支在正侧的边值，则在z=c 附近有

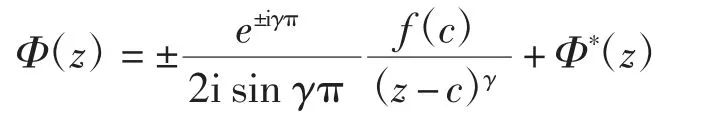
其中：正号或负号随c=a 或b 而定，Φ*（z）则在z=c的剖开的邻域中全纯，并且

（1）若α=0，则当z 以任何方式趋于c 时，Φ*（z）有确定的极限。

（2）若 α ＞ 0，则在 z=c 附近，下式成立

可知此时Cauchy 型积分满足下式

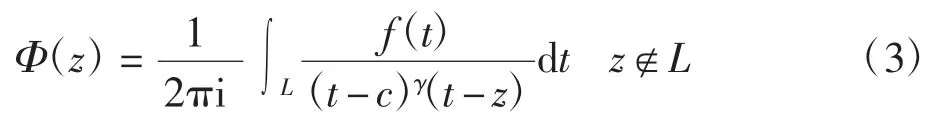
在z=c 附近，有下述表达式成立

其中：εj=+1，若 c 为 Lj的起点，εj=-1，若 c 为 Lj的终点，而Φ*（z）在沿各lj剖开后的的c 邻域中全纯，且Φ*（z）在z=c 附近仍有文献[1]中所述性质。

改写式（4）为

接下来将分区域考虑[（t-c）γ]j的取值。

需注意（t-c）γ为（z-c）γ当 z 从 L 的正（左）侧趋于L 上一点t 时的极限值，故可记[（t-c）γ]+=（t-c）γ。

当区域位于L 右侧时，则需要相应的考虑[（t-c）γ]-的取值。若t 从其正侧绕点c 反时针转一圈到达L 上同一位置 t 时，θ=arg（t-c）增加了 2π；若 t 从其正侧绕点c 顺时针转一圈，则θ=arg（t-c）减少2π。

2.2 特殊条件下端点奇异性分析

为了更清晰地体现曲线叠加可能产生的在节点处的奇异性变化并方便计算，首先考虑在一些特殊条件下该节点具有的端点奇异性，再将其推广至一般条件进行探索。

Ⅰ.给定fj（t）在整个复平面上解析，即fj（c）在Lj上属于H。令各Lj上t→c 时fj（c）的极限值相同

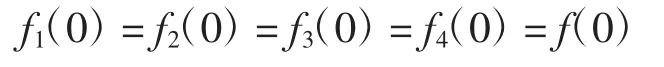
（1）在区域①中，根据曲线方向判断，[（z）γ]1=e-2πiγtγ、[（z）γ]2= e2πiγtγ、[（z）γ]3= tγ、[（z）γ]4= tγ，代入上式Φ（z）表达式中，化简计算可得

已知Φ*（z）全纯，故此时Φ（z）由区域①趋向c时，c 点处没有奇异性，解析。

（2）在区域②中，根据曲线方向判断，[（z）γ]1= tγ、[（z）γ]2= tγ、[（z）γ]3= e2πiγtγ、[（z）γ]4= e-2πiγtγ，代入上式Φ（z）表达式中，同理化简计算可得：Φ2（z）=Φ*（z），已知Φ*（z）全纯，故此时Φ（z）由区域②趋向c 时，c 点处没有奇异性，解析。

（3）在区域③中，根据曲线方向判断，[（z）γ]1= tγ、[（z）γ]2= e2πiγtγ、[（z）γ]3= tγ、[（z）γ]4= tγ，代入上式Φ（z）表达式中，化简计算可得

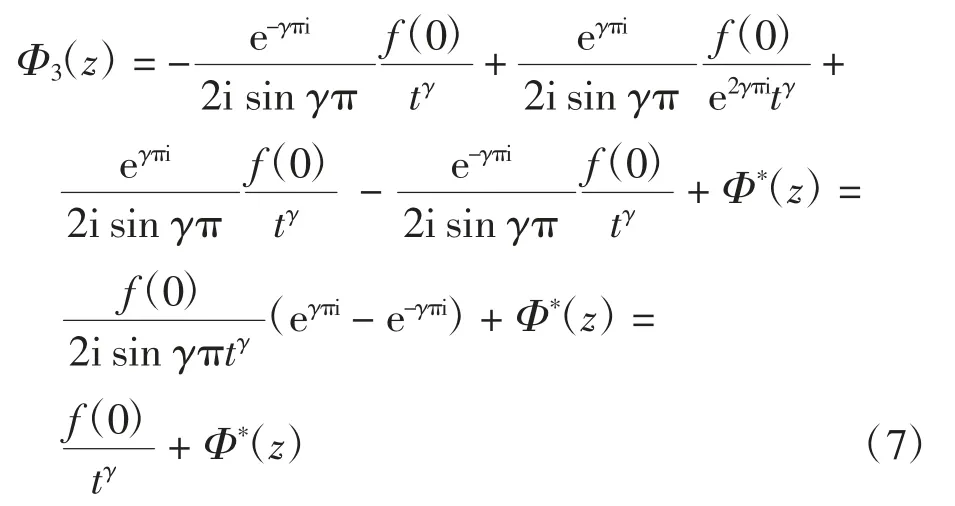
已知Φ*（z）全纯，故此时由区域③趋向c 时，c 点处有γ 阶奇异性。

（4）在区域④中，根据曲线方向判断，[（z）γ]1=e-2πiγtγ，[（z）γ]2=tγ，[（z）γ]3=tγ，[（z）γ]4=tγ，代入上式Φ（z）表达式中，同理化简计算可得

已知Φ*（z）全纯，故此时Φ（z）由区域④趋向c时，c 点处有阶奇异性。

Ⅱ.假设f3- f1= f4- f2，即割破线以上曲线上的fj（t）在节点的函数和（方向不同则为差）与割破线下方曲线上fj（t）函数的和（方向不同则为差）相等。

以区域①中为例，各[（t-c）γ]j取值与Ⅰ中相同，此时

可知此时 Φ（z）由区域①趋向 c 时，c 点处有 γ 阶奇异性。

下面相应的考虑其他区域的情况：

（1）Φ（z）由区域②趋向 c 时

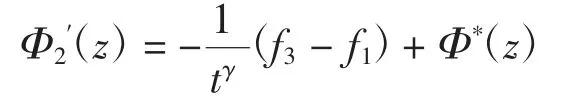
（2）Φ（z）由区域③趋向 c 时

（3）Φ（z）由区域④趋向 c 时

可见在条件Ⅱ下，当Φ（z）由任意区域趋向c 时，均有γ 阶奇异性。

3 结 论

定理1 给定fj（t）在整个复平面上解析，即fj（c）在lj上属于H。令各lj上t→c 时fj（c）的极限值相同：即f1（0）=f2（0）=f3（0）=f4（0）=f（0），则关于节点处的奇异性有以下结论。

（1）由区域①和②趋向于节点时，由于曲线方向关系，此时节点处奇异性抵消。

（2）由区域③和④趋向于节点时，此时曲线方向不足以抵消奇异性，节点处有γ 阶奇异性。

定理2 给定条件：f3- f1= f4- f2，即割破线上方曲线上的fj（t）在节点的函数和（方向不同则为差）与割破线下方曲线上fj（t）函数的和（方向不同则为差）相等。对于本文给定的特殊曲线，当Φ（z）由任意区域趋向c 时，节点c 处均有γ 阶奇异性。