基于竞争侵略策略的粒子群算法

安 宁，张 军，季伟东

（哈尔滨师范大学 计算机科学与信息工程学院，哈尔滨 150025）

0 引言

群体智能是模拟自然界生物群体行为而构造的随机优化算法，它为解决约束性、非线性和求极值等问题提供了新的思路。遗传算法［1］、蚁群算法［2］与粒子群优化（Particle Swarm Optimization，PSO）算法［3］是群体智能中重要的3 种方法。其中PSO 算法概念简明、易于实现、参数设置少，是一种高效的搜索算法。但在算法迭代后期，粒子群算法容易陷入局部最优且收敛速度较慢。为了提高算法性能，涌现出不同思想的优化策略。在基本粒子群算法进化方程的改进方面，Shi Y［4］在惯性权重的基础上，提出模糊系统动态调整惯性权重策略；Taherkhani M［5］等根据每个粒子与最优位置的距离和粒子性能，赋予每个粒子在不同维度上的惯性权重，实现了惯性权重的动态调整。惯性权重的调整可以平衡算法全局搜索与局部搜索能力，但对于提升算法后期，收敛速度仍有欠缺。胡旺［6］等将简化粒子速度更新策略应用于一种更简化而高效的粒子群优化算法。该算法删除粒子速度项，将二阶微分方程简化为一阶微分方程，大幅度的减少了算法的运行时间。同样，在改变速度更新策略方面，El-Sherbiny［7］提出无速度方程的粒子群优化算法。该算法中每个粒子的新位置直接由个体与群体最佳位置的不同线性组合来确定，用较少的迭代次数寻到较优的解。在借鉴其它优化策略方面，Clerc［8］等为保证算法的收敛效果，在粒子群算法中引入收缩因子，但收缩因子能力有限，不能较好的平衡全局搜索和局部搜索。为了解决该问题，Wang F［9］等将自适应学习策略应用到粒子群算法中，提出自主学习的候选生成策略与竞争学习的预测策略，同时制定了一种自适应的寻优方向调整机制，更好的平衡全局搜索能力和局部搜索能力。该算法中竞争学习的预测策略提供了一种粒子间竞争学习的思路。随着多种群策略的提出，衍生出大量多种群协同寻优的改进算法。2018年，邓先礼［10］等在多种群同步进化的基础上，赋予子种群不同的搜索特性，利用各子种群性能的周期性评价指导个体进行迁移，实现种群间的合作；Niu B［11］在种群合作的基础上，提出种群内部和种群之间两种社会活动，在进化过程中粒子不仅与自身种群的其他粒子交换社会经验，而且还受到其他种群粒子经验的影响，该策略增强了粒子的学习能力。文献［12］将反向学习策略与局部学习策略结合，当算法陷入局部最优时，利用较差粒子的位置信息指导部分粒子以较快的飞行速度进行反向学习，跳出局部最优；罗强［13］等将反向学习策略与最优粒子策略结合，利用全局最优粒子进行反向学习，通过全局最优粒子的更新引领粒子向更好的位置飞行，加强算法多样性的同时拥有较高的收敛速度。为提高算法的收敛速度与摆脱局部最优的能力，各种算法提出了不同的改进策略，文献中的算法在提高算法收敛速度或摆脱局部最优状态过程中，都存在一方面的效果比较显著，但在另一方面表现稍差的现象。

本文提出一种基于竞争侵略策略的粒子群算法（CAPSO）。受最优粒子策略与竞争学习策略启发，将种群分类、最优粒子与竞争学习思想应用于算法中，定义了侵略性自由粒子和竞争池两个概念。侵略性自由粒子与竞争池挑选竞争最优粒子，利用竞争最优粒子简化传统速度公式并指导择优进化群更新。为验证CAPSO 算法在提高算法收敛速度与摆脱局部最优能力方面的性能，将其与4 种经典算法（RLPSO［12］算法、TDDALFPSO［14］算法、ScDCPS 算法［15］、IPSO 算法［16］，）进行对比。其中，RLPSO 算法在最优粒子与竞争学习方面进行改进；TDDALFPSO 算法在自适应学习方面进行改进；ScDCPS 算法在种群分类与种群控制方面进行改进；IPSO 算法在粒子学习机制上采用了竞争策略，与CAPSO 算法形成多方面的对比。在8 个标准测试函数下进行仿真实验，结果表明CAPSO 算法具有较快的收敛速度和较高的求解精度。

1 基于竞争侵略策略的粒子群算法（CAPSO）

CAPSO 算法将种群划分为规模相同的二部分：一部分为侵略性自由粒子群，另一部分为择优进化群。二部分粒子遵循不同的更新规则，侵略性自由粒子群遵循高自由度参数更新原则，择优进化群遵循改进速度公式进行更新。在CAPSO 算法的每次迭代过程中，侵略性自由粒子群中随机选择一个粒子与择优进化群进行一次适应度值竞争，获胜的粒子作为竞争最优（Cbest）存入竞争池中，并利用该粒子指导择优进化群进行下一次迭代。此策略增强了算法摆脱局部最优的能力，且算法的收敛速度有较大提高。近年来也涌现出很多结合竞争策略的粒子群优化算法。如2015 年，Cheng R［17］提出的大规模优化的竞争群优化算法，在所有粒子中随机挑选两个粒子成对进行竞争学习，失败的粒子直接向获胜的粒子进行学习，在粒子更新的过程中个体最优与全局最优不参与更新过程；2019 年，刘明［18］等将竞争策略与周期性结合，即每隔一定迭代次数运用一次竞争学习机制，竞争机制的原理与Cheng R 提出的竞争原理相似，同样是竞争失败的粒子向获胜的粒子学习。上述二种算法中均省去了历史位置的记录，算法中个体最优与全局最优历史位置仍存在，但不参与算法迭代。本文提出的CAPSO 算法中，已经完全摒弃了个体最优与全局最优的概念，利用竞争最优粒子直接指导择优进化群更新。在竞争策略方面，CAPSO 算法将所有粒子分为不同更新规则的二个种群，与上述二种算法竞争策略的不同之处为：

（1）CAPSO 算法为二个不同种群间的粒子竞争，而不是同种群内相同更新规则的粒子间竞争。

（2）获胜的粒子定义为竞争最优，指导择优进化群的更新，而不是指导失败粒子进行更新。

1.1 竞争池

竞争池存储竞争最优（Cbest）粒子的位置信息，空间大小为N／2。竞争最优指每一代更新过程中，侵略性自由粒子与择优进化群中的粒子进行适应度值的竞争，获胜的粒子定义为竞争最优，并将位置信息保存在竞争池中。竞争最优存入竞争池后，择优进化群的下一代更新需在竞争池中取出当代竞争最优的位置信息，来指导择优进化群进行下一次更新。位置信息取出后，竞争池中仍保存每代竞争最优的位置信息。为保证择优进化群第一次更新，初始所有粒子后，选择适应度值最优的粒子作为第一个竞争最优并存入竞争池。由于竞争最优的选择机制，保证了竞争最优的粒子信息为每一代全部粒子的最优信息。竞争池的存在为改进速度公式打下基础，将传统的粒子群算法中的个体最优和全局最优用竞争最优替代，以达到简化传统速度公式的目的。图1 及图2 为竞争最优的选择与指导择优进化群的二维示意图。

图中：U 是解空间；三角形和圆形分别代表侵略性自由粒子和择优进化群中的粒子；Cbest 是竞争最优；五角星是需要寻找的理论解。

图1 中，侵略性自由粒子距离理论解较近，代表适应度值更优，故侵略性自由粒子作为竞争最优并存入竞争池中。相反，若择优进化群的粒子距离理论解较近，则择优进化群的粒子作为竞争最优并存入竞争池中；图2 中，①为在竞争池中取出竞争最优的位置信息，②为竞争最优指导择优进化群更新。

图1 竞争最优入池示意图Fig.1 Schematic diagram of competition for optimal entry into the pool

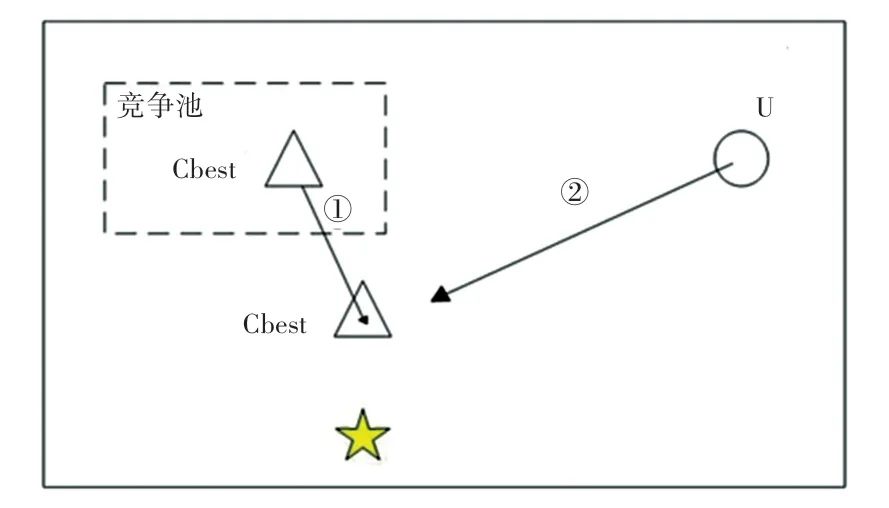
图2 竞争最优出池示意图Fig.2 Schematic diagram of competitive optimal pool

1.2 侵略性自由粒子

初始设定N个粒子，当N为偶数，即选取N／2 个粒子作为侵略性自由粒子；当N为奇数时，随机选取一个粒子，定义该粒子即是侵略性自由粒子，也是择优进化群中的粒子。此策略可保证侵略性自由粒子与择优进化群的规模保持一致。侵略性自由粒子具备高自由度和侵略性。

1.2.1 高自由度

本文设置为D 维，粒子初始赋予位置信息。大部分随机优化算法（包括粒子群算法和遗传算法等）对于粒子的更新多数是D 维，采用相同的参数更新。本文侵略性自由粒子，在粒子所具有D 维的基础上，各维逐一与相对应的高自由度参数进行更新。以此更新策略为前提，为保证侵略性自由粒子的每次更新不超出预设边界，高自由度参数设置为［-1，1］之间的随机数，由此改变粒子位置，该策略增强了算法的多样性。更新过程如图3 所示：（其中：Xi 为各维的位置信息，Ri 是随着Xi 逐一生成的高自由度参数，1 ≤i≤D。）

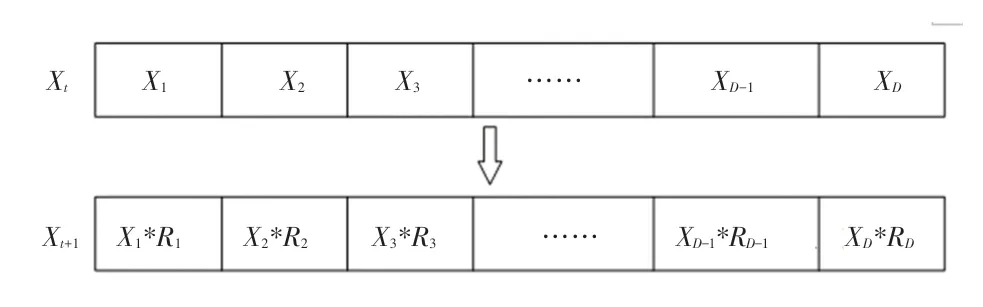
图3 侵略性自由粒子更新示意图Fig.3 Update diagram of aggressive free particles

1.2.2 侵略性

自由粒子的侵略性体现在粒子群的优化更新过程中。当择优进化群的粒子在适应度值竞争中获胜作为竞争最优时，侵略性未被激活，择优进化群按原有轨迹进行更新；当侵略性自由粒子在适应度值竞争中获胜作为竞争最优时，激活侵略性。此时侵略性自由粒子以改进速度公式作为载体，参与择优进化群的更新过程，指导择优进化群向侵略性自由粒子的位置信息进行学习，使择优进化群摆脱原有更新轨迹。该策略增强了算法摆脱局部最优的能力。

1.3 改进速度公式

传统粒子群算法（PSO）的速度更新公式中，存在个体最优与全局最优两个概念。本文提出的算法凭借竞争最优（Cbest）的选择机制，摒弃个体最优与全局最优，将原有的两个外部存档，优化为仅对竞争最优进行外部存档，降低了算法的空间复杂度。算法在粒子速度更新时，仅向竞争最优进行学习，提高粒子的学习精度。对比传统速度公式，改进后的速度公式提高了算法的运算速度，将算法效率进一步提升。速度公式如式（1）所示。

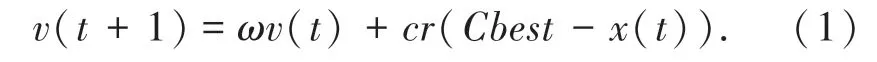
2 实验结果分析

通过对8 个典型标准函数的测试，对比CAPSO算法和其它改进算法的性能。其中f1～f4 为单峰函数；f5～f8为多峰函数，具体函数见表1。

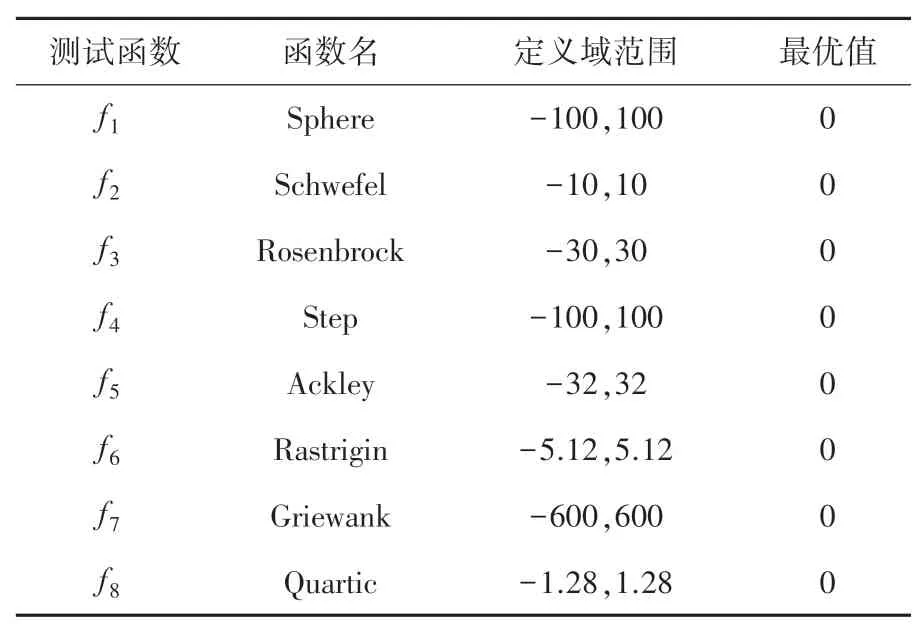
表1 标准测试函数Tab.1 Standard test functions

参数设置：维数D＝30、种群规模N＝50、最大迭代次数为1 000、c＝2、r为［0，1］之间的随机数、ω最大值为0.9、最小值为0.4；每个算法计算10 次，最优解取平均值。

通过Matlab 仿真，得到不同算法在8 个标准测试函数的收敛曲线如图4、图5，各算法测试结果见表2。

表2 不同算法在8 个标准测试函数中的结果Tab.2 Results of different algorithms in 8 standard test functions

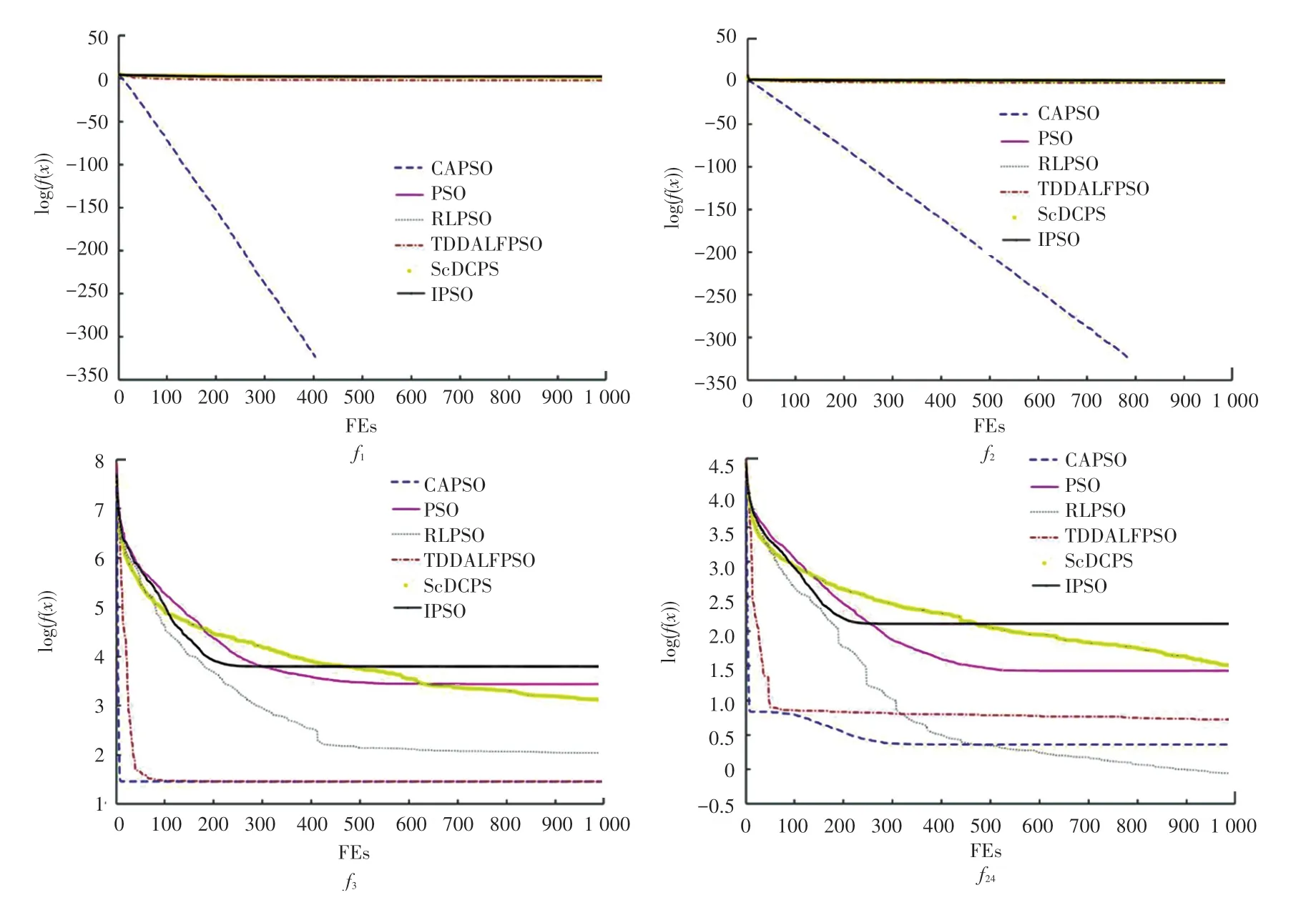
图4 不同算法在4 个单峰标准测试函数的收敛曲线Fig.4 Convergence curves of different algorithms on four unimodal standard test functions

函数f1、f2是简单的单峰测试函数，CAPSO 算法可以直接寻优。函数f1进化次数为420 次寻优，函数f2进化次数为800 次寻优。在图像f1与图像f2中，CAPSO 对比其余五种算法，在收敛速度与收敛精度方面，性能大幅提升，造成图像重叠；而在表2中可以看出，RLPSO 算法与TDDALFPSO 算法在精度上优于PSO 与ScDCPS 算法。结合f1与f2图像可知，竞争池机制发挥了重要作用，保证算法的每次更新都向最优的粒子学习，算法寻优精度提升明显；函数f3和f4稍复杂，CAPSO 算法未寻到最优值，相对比其它算法收敛精度较高。在f3图像中可以看出CAPSO 算法与TDDALFPSO 算法在收敛精度上几乎一致，但CAPSO 算法的收敛速度更快；在f4图像中，收敛精度最高的是RLPSO 算法，但CAPSO 算法的收敛速度更快，弥补了收敛精度稍差的劣势。结合f3图像和f4图像，通过ScDCPS 算法与PSO 算法对比，可以得出ScDCPS 算法牺牲收敛速度来提高收敛精度，在此基础上收敛精度仍不如RLPSO 算法。通过4 个单峰测试函数可得到，CAPSO 算法对比其他改进算法收敛速度更快，收敛精度较高。CAPSO 算法在单峰函数求解问题上性能较优。

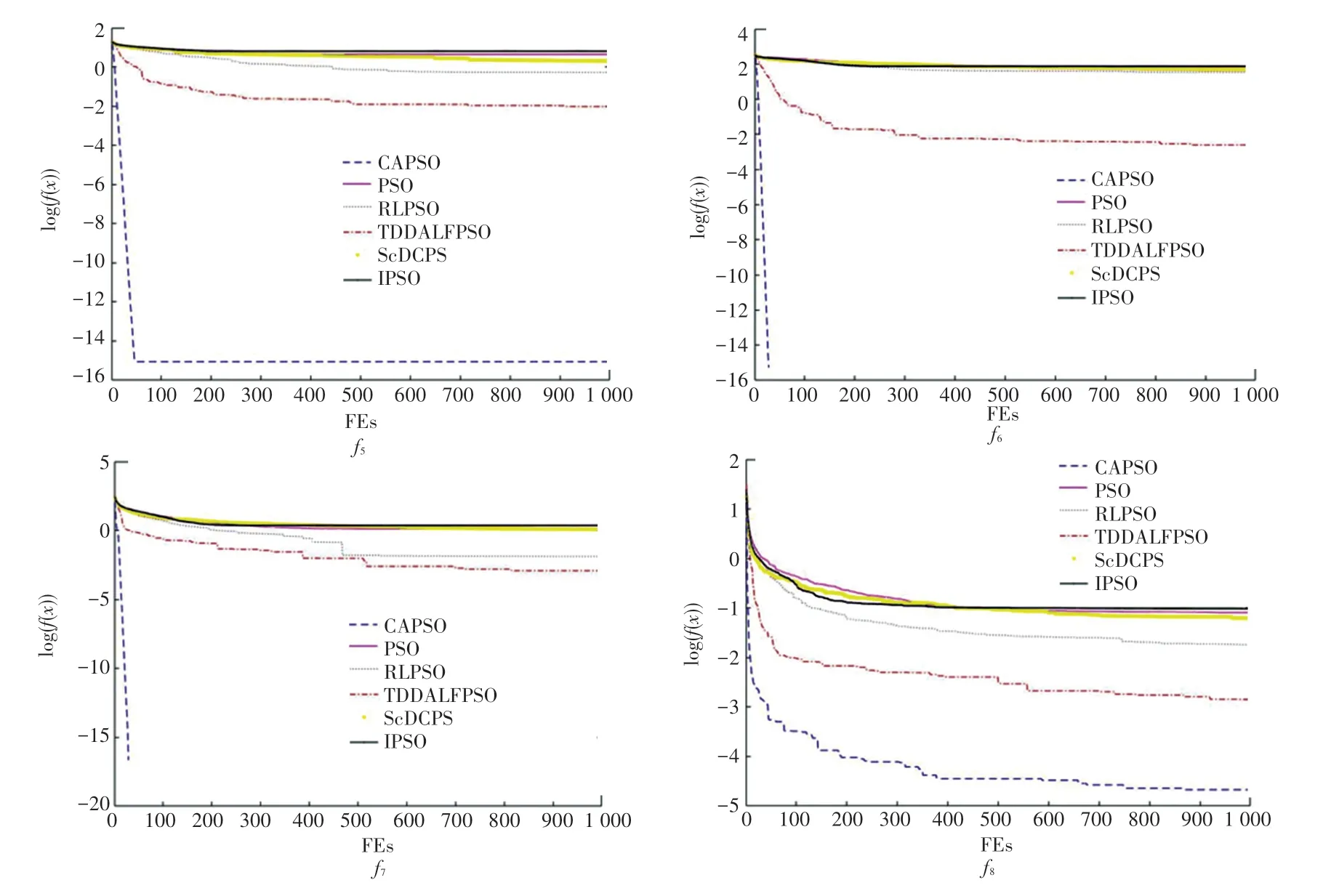
图5 不同算法在4 个多峰标准测试函数的收敛曲线Fig.5 Convergence curves of different algorithms on four multi-peak standard test functions

函数f5～函数f8为较复杂的多峰函数，在f5～f8的4 张图像中，可直观的观察到CAPSO 算法无论在收敛速度上，还是收敛精度上都保持最优，而在函数f6和函数f7，CAPSO 算法可以直接寻优。函数f6进化次数为32 次寻优，函数f7进化次数为32 次寻优。在函数f5的测试结果中，CAPSO 算法最优，PSO 算法、RLPSO 算法与ScDCPS 算法在收敛速度和精度上相差较小，TDDALFPSO 算法略优，但对比CAPSO 算法存在较大差距。在函数f8的测试结果中，CAPSO 算法同样优于其它算法，虽然有短暂陷入局部最优的情况，但侵略性自由粒子凭借自身高自由度的特性，迅速令算法摆脱局部最优的情况，并且在1 000 次进化后，仍有下降的趋势。TDDALFPSO 算法优于RLPSO算法，ScDCPS 算法略优于PSO 算法。CAPSO 算法在多峰函数求解问题上，性能同样较优。

由上述对比可知，经过改进的CAPSO 算法，无论在单峰函数问题还是多峰函数问题，总体性能相比较PSO 算法以及其他思想改进方式的RLPSO 算法、TDDALFPSO 算法、ScDCPS 算法和IPSO 算法，有较大的提升。与IPSO 算法的对比可以得出，经本文优化后的竞争侵略策略对比IPSO 算法的竞争策略性能更优，种群间的粒子竞争机制发挥着重要作用。从表2 的数据方差中也可看出，在多数测试函数中CAPSO 算法的方差值较小，算法稳定性较高。

3 结束语

本文结合多种改进策略，提出基于竞争侵略策略的粒子群算法（CAPSO），该算法利用侵略性自由粒子的高自由度特性结合竞争池概念，大幅度的提升了算法的性能。CAPSO 算法在避免陷入局部最优和提高收敛速度的问题上表现出较强的能力，通过竞争最优（Cbest）的选择机制，摒弃个体最优与全局最优，达到简化速度公式的目的，令算法进化过程中更新速度更快，学习效率更高，在单峰函数和多峰函数中都具有优秀的收敛速度和收敛精度，且算法稳定，证明CAPSO 算法的机制可以解决多种优化问题。