航空弹药实弹打靶安全距离评估方法

孔凡成，张孝虎，周弘扬,王为奎,谢全民

(1．空军勤务学院弹药系，江苏 徐州 221000；2．陆军工程大学军械士官学校弹药系，武汉 430000)

近年来，部队实战化训练与实弹打靶任务增多，打靶时弹体落地的弹着点(弹体落地点)与观众观测台间距离 (安全距离)的评估是实弹打靶中面临的现实问题。

安全距离因弹药种类的不同而不同，不合适的距离将危及观测台的人员安全，必须对安全距离进行预先评估。过去对安全距离的评估缺少严格的理论分析与计算，主要采用估算法，结果不准确，给现场实弹打靶留下了严重隐患。认真研究航空弹药实弹打靶安全距离评估方法，可以为实战训练提供现场评估手段，解决部队实战化训练面临的实际难题。

1 实弹打靶概况

某大型实弹打靶概况如图1所示，2条黑实线代表大峡谷，大峡谷两侧分别是山脉与沼泽地，黑色箭头表示战机由左向右飞行；需要打击峡谷内A、B、C模拟目标。A目标为机场，尺寸为50 m×50 m×0.4 m，即厚度0.4 m的钢筋混凝土跑道目标，距离观测台(F)4.1 km；B目标为敌指挥所目标，为3层钢筋混凝土建筑物，距离观测台(F)3.5 km；C目标为敌导弹技术阵地，为3个真实的地空导弹发射架，发射架为厚度20 mm钢制目标，距离观测台(F)4.3 km。从3个目标的位置看，B目标弹着点距离观测台(F)最近，打靶时破片飞散距离很可能会超过3.5 km，威胁观众人身安全，必须进行安全距离评估。

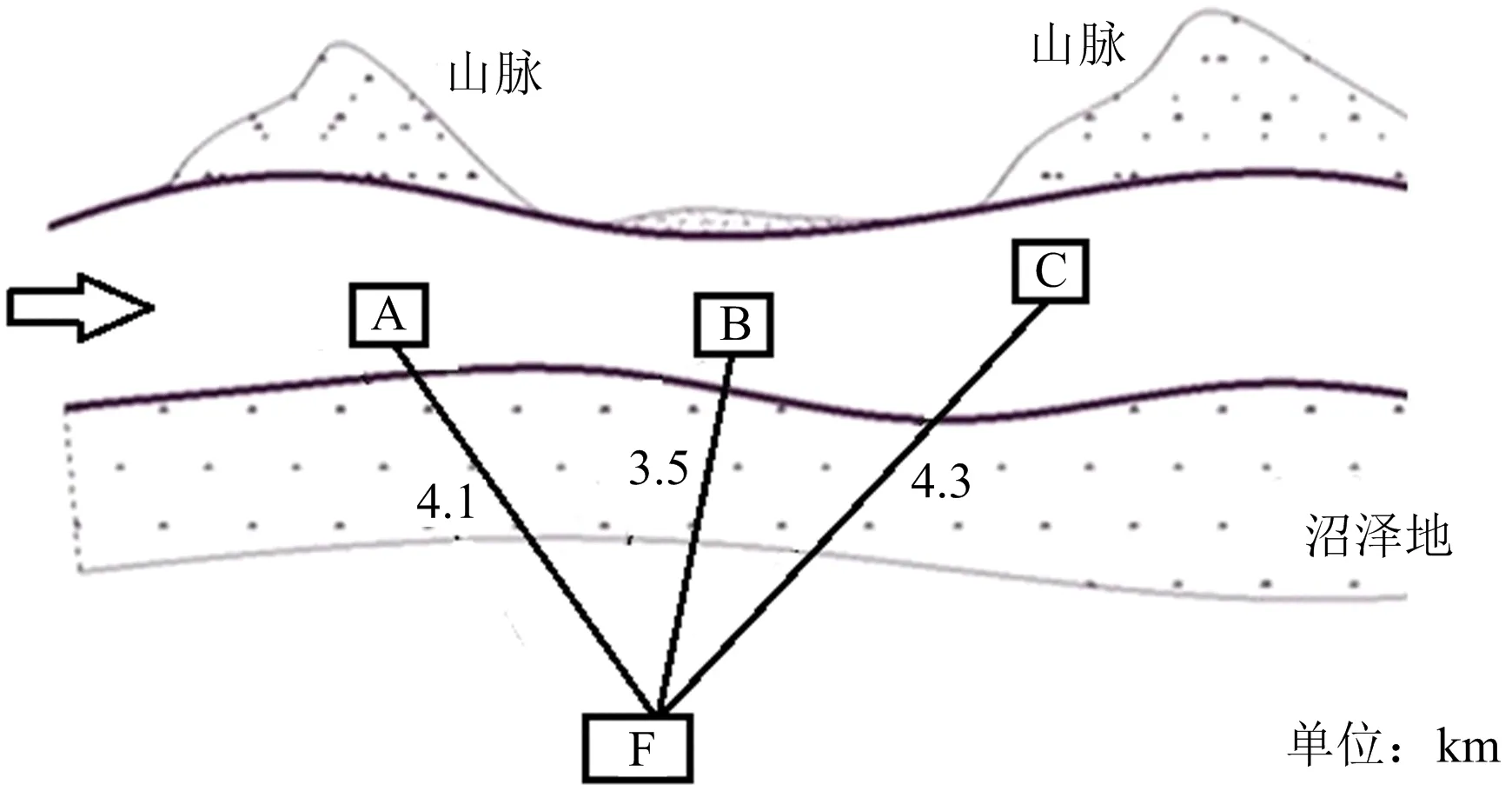
图1 实弹打靶位置Fig.1 Location of live-fire target

2 安全距离

航空弹药实弹打靶属于壳体装药在土岩介质中爆炸，基于弹药爆炸理论，从爆源(弹着点)起爆来看，弹药主要经历3个阶段[1]：冲击波、应力波与地震波，即存在3种破坏效应(见图2～3);存在3个安全距离：冲击波安全距离、破片飞散安全距离、振动安全作用距离。

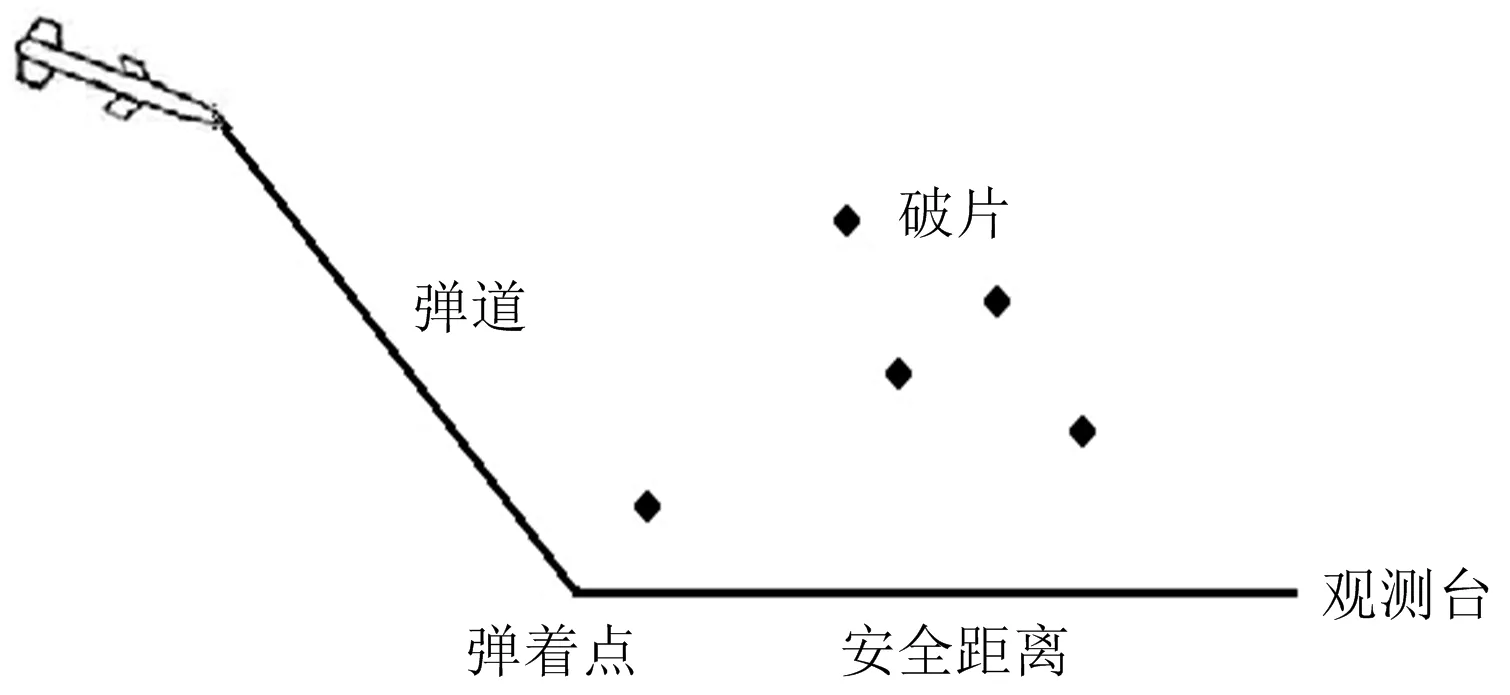
图2 安全距离Fig.2 Safe distance

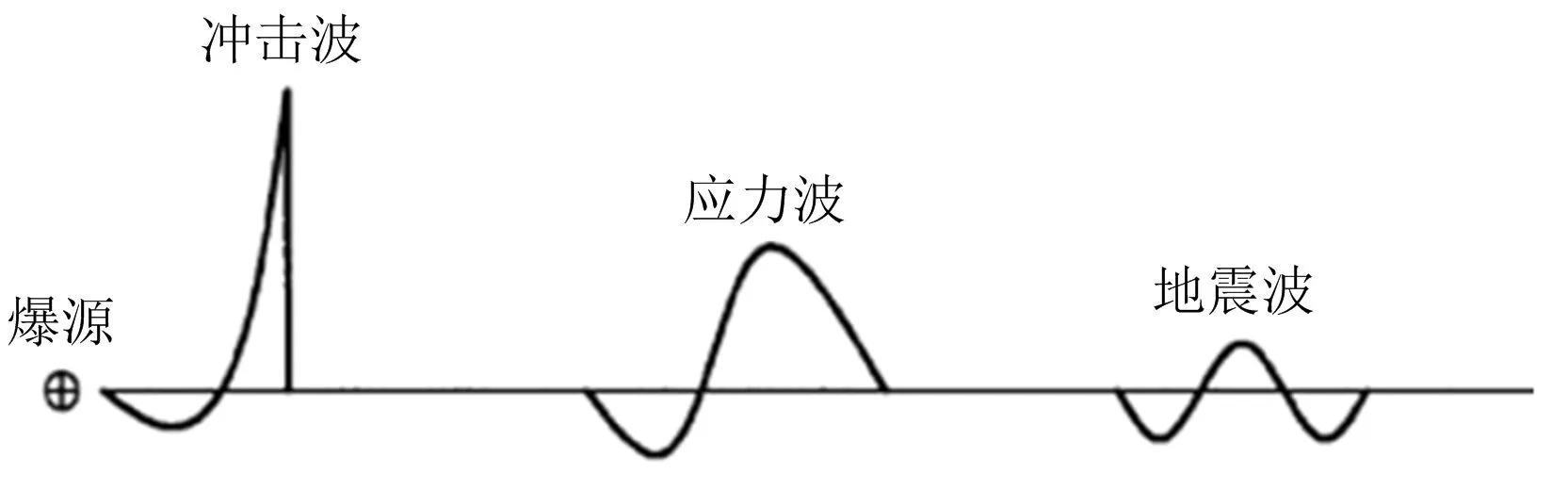
图3 常规弹药爆炸破坏效应Fig.3 Destructive effect of conventional ammunition

2.1 冲击波安全距离

冲击波安全距离是保证人员与结构物不受冲击波伤害时距离弹着点的最小允许距离。冲击波对人员的安全距离为[2]

(1)

式中:Rc为冲击波对人员的安全距离，m；Q为弹药装药量，kg。

Rc与Q关系如图4所示。

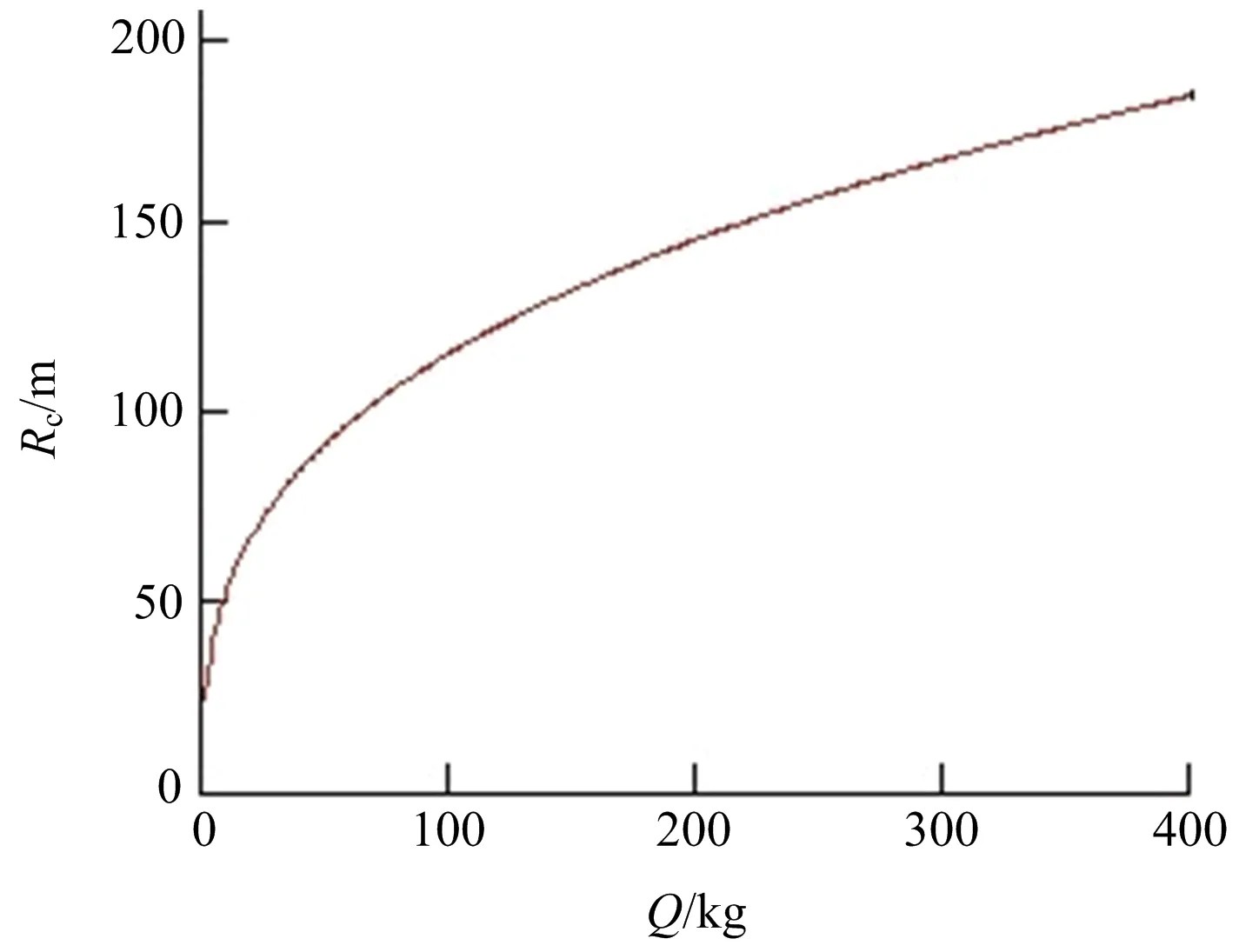
图4 Rc与Q关系Fig.4 Relationship between Rc and Q

2.2 振动安全作用距离

根据弹药爆炸与爆破振动经典公式(萨道夫公式)[3]：

(2)

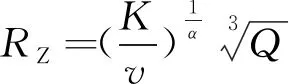
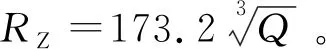
振动安全作用距离RZ与Q关系如图5所示。

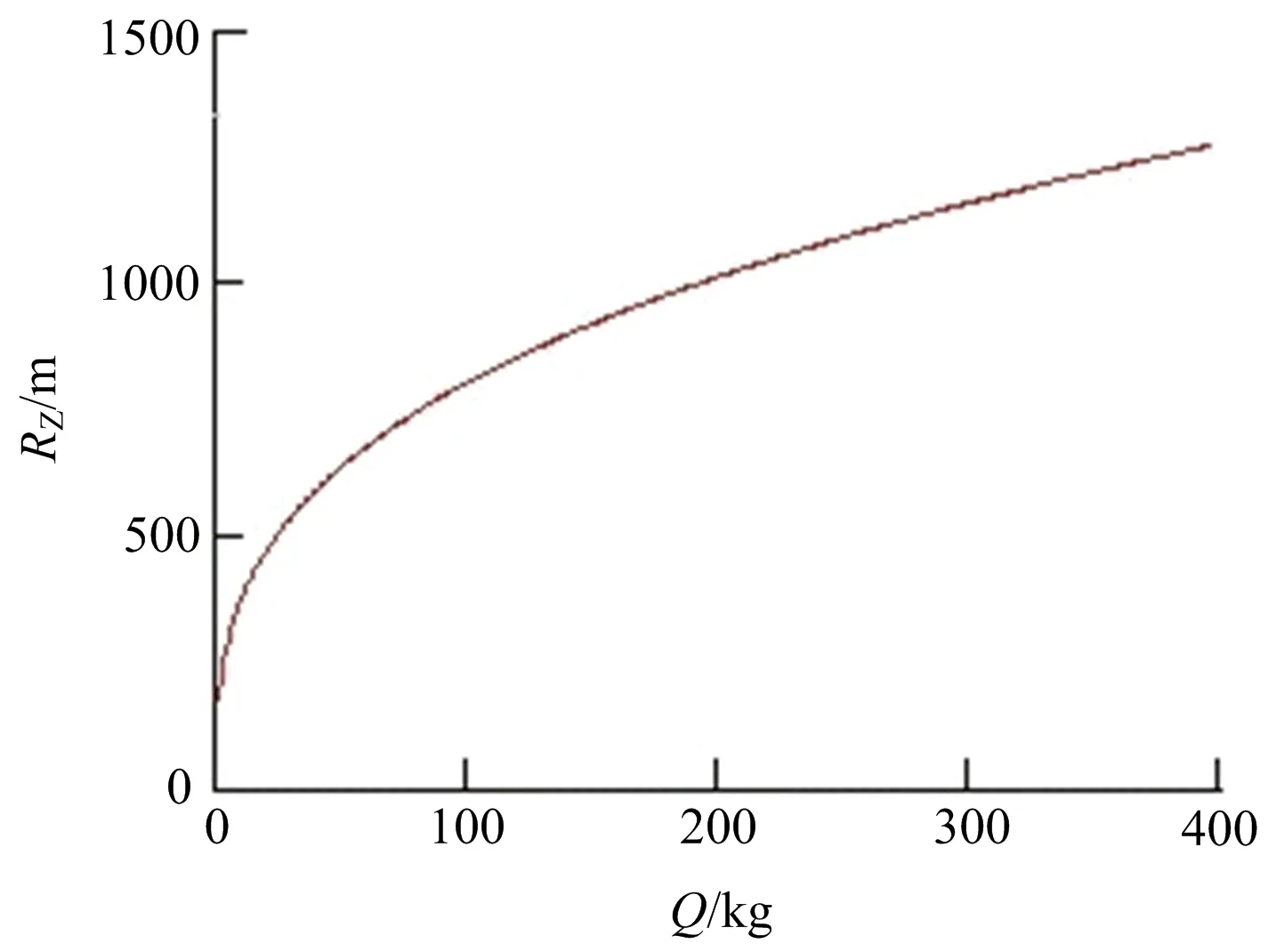
图5 RZ与Q关系Fig.5 Relationship between RZ and Q

2.3 破片飞散距离

破片飞散距离的影响因素与计算方法较多，从装药量与破片飞散距离关系方面，初步估值可以参考文献[4-5]，其关系为

(3)

RP与Q关系如图6所示。

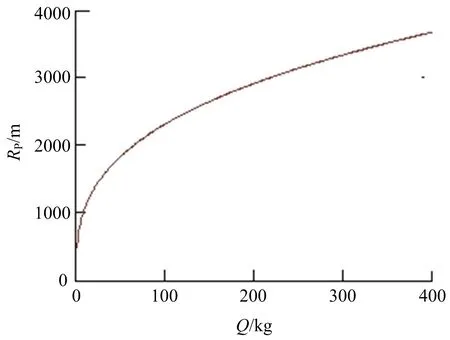
图6 RP与Q关系Fig.6 Relationship between RP and Q

比较式(1)～(3)，可以发现，Rc∶RZ∶RP=1∶6.9∶20，比较图4～图6可以发现，在装药量Q相同的条件下，RP最大，即破片飞散距离最大。只要满足破片安全距离，冲击波安全距离与振动安全距离可以忽略不计，即破片安全距离为主要考虑对象。

3 破片飞散安全距离

3.1 估算法

1)按照弹重估算。在不知道装药量的情况下，破片飞散距离一般先按照弹重或弹径估算安全距离，弹重与安全距离关系如表1所示。

表1 弹重与安全距离关系

2)按照弹径估算。航空弹药破片飞散安全距离Rp大致为弹径的10 000倍[6]。

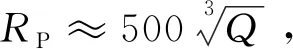
3.2 工程近似法

弹药爆炸后产生破片，破片获得初速后，即在空中飞行，破片运动与飞行弹道如图7所示，由于破片飞行时间较短，可以认为是直线，直线达到最高点时的水平距离，即认为是破片飞散距离的一半[7]。

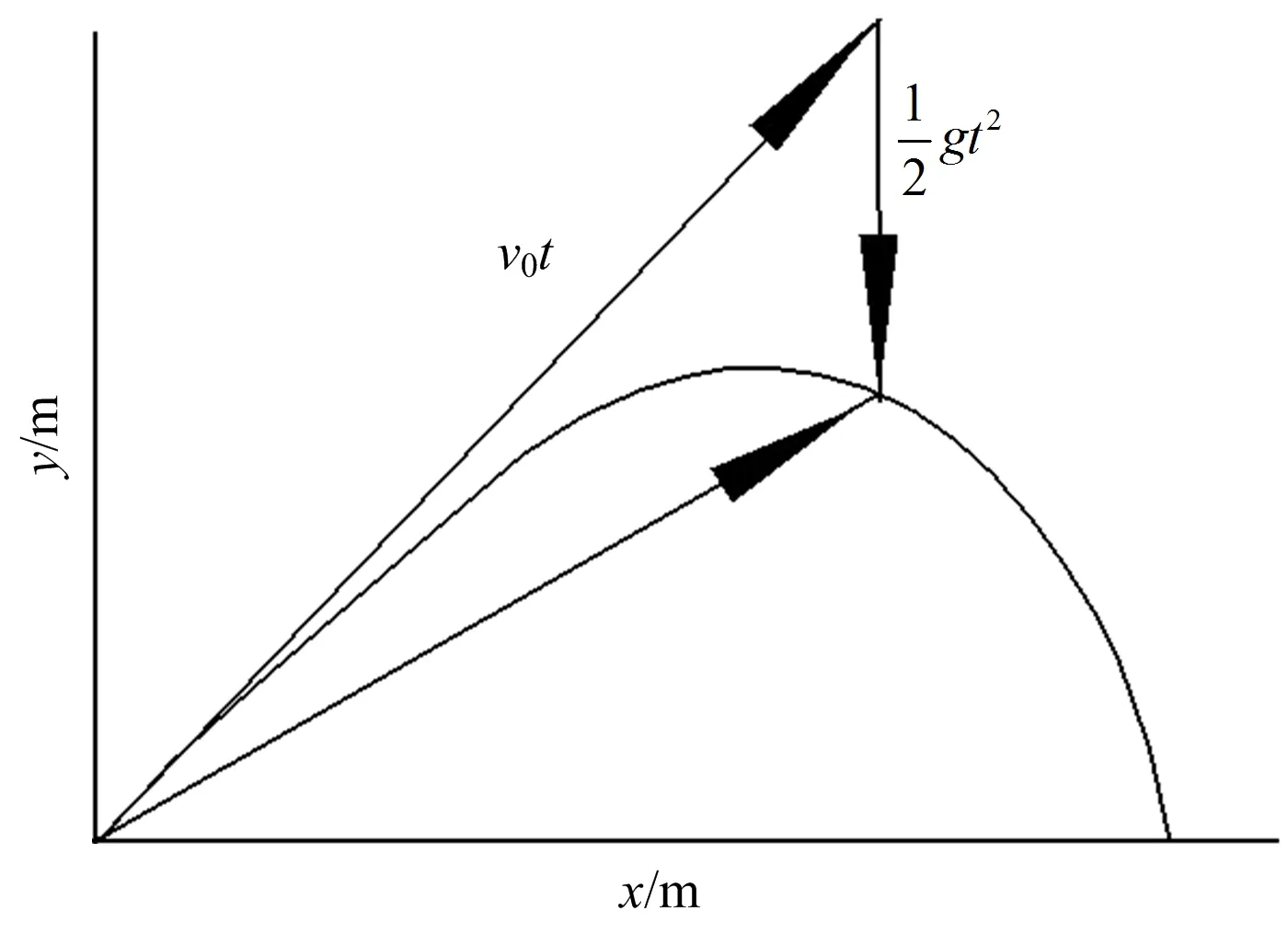
图7 破片运动轨迹Fig.7 Breaking motion trajectory

基于前人推导与计算[4]，飞散距离的一半为

(4)

式中：x为破片某瞬时距炸点的距离，m；vx为x距离时的破片速度(简称存速)；v0为破片初速。

其中，G为格尼系数，m/s(见表2)；β为装药系数；w为装药质量，kg；wc为弹壳质量，kg。

表2 炸药格尼常数

Me为破片质量(g)，破片质量分为9个等级：1～4、4～8、8～12、12～16、16～20、20～30、30～50、50～100、100～200 g；CD为破片迎风阻力系数(见表3)；

表3 破片迎风阻力系数[8]

ρ为当地空气密度,是破片在飞行高度中的气体密度,ρ随海平面高度y而定,ρ=ρ0h(y)，ρ0为海平面空气密度，海平面处ρ0=1.226 kg/m3，h(y)为空气密度随海拔高度变化的密度函数，其值为

(5)

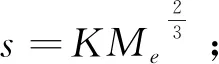
表4 各类钢制破片K值

某型航空炸弹(质量217.5 kg，装药量90.5 kg，弹径229 mm)，则：

=2402×0.706

=1695 m/s

生长在“酒糟透之人”这样的原生家庭里，即使不变得尖酸刻薄，也难免会被生活染上一层风霜，断不可能有眼前的淡定从容之态。

vx取一个不为零的小值，取vx=0.01 m/s[9],取Me=20×10-3kg，CD=1.15，K=3.5×10-3，g=9.81 m/s2，则:

=1350 m

则破片安全距离为2x=2 700 m。

3.3 仿真数据拟合法

根据前人对于爆炸冲击现象的数值模拟结果[10]，对爆炸破片飞散仿真数据回归处理，并进行数据拟合，得到破片飞散速度仿真数据拟合公式[10]：

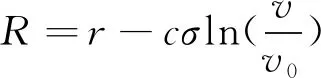
(6)

式中:R是飞散距离的一半，m；r为弹径，m；C=943.5-1597.5ε+718.7ε2；

式中：μ=1～3，为破片系数，反映破片尺寸大小；V01为破片体积；δ为弹壳厚度。

R随μ变化，R=f(μ)，在Mathcad 2000环境下绘制R=f(μ)曲线[11](见图8)。当μ=3时，R取得最大。

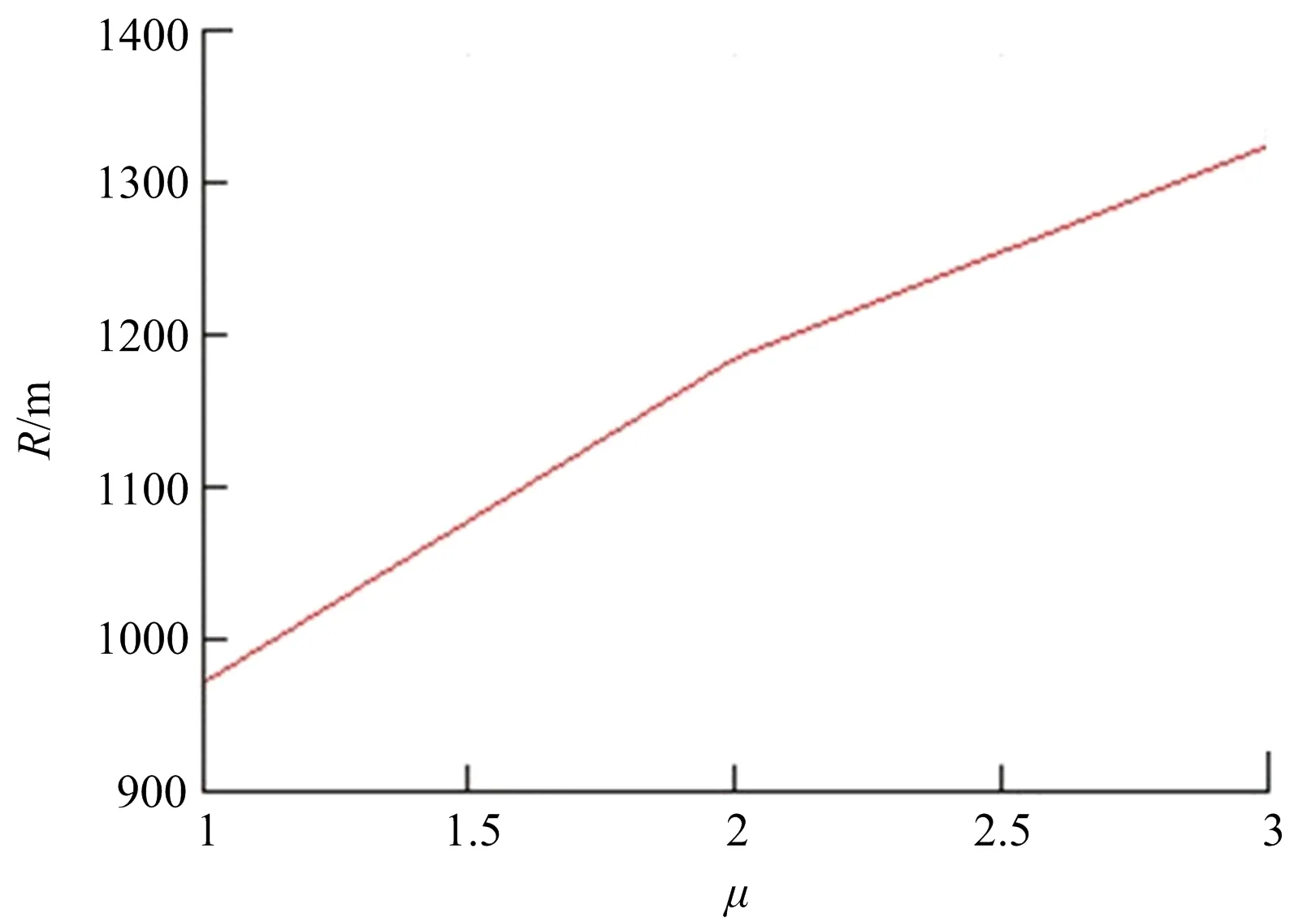
图8 R=f(μ)曲线Fig.8 Curve of R=f(μ)

以某粗短型航空炸弹(重217.5 kg，装药量90.5 kg，弹径229 mm)为例，对粗短型弹药采用仿真数据拟合公式进行计算。

C=943.5-1597.5ε+718.7ε2=128

=0.867

=1 324 m

破片安全距离为2R=1 324×2=2 648 (m)

某细长型弹药长度4 900 mm，质量为700 kg，其中战斗部长度1 169 mm，弹体(战斗部)直径380 mm，质量320 kg；主装药质量107 kg。计算方法与粗短型相同，主要区别是计算参数仅为战斗部参数，按照上述数据拟合计算方法其破片飞散距离为2R=1 240×2=2 480 m。

不同评估方法的破片飞散距离计算结果与比较如表5所示。

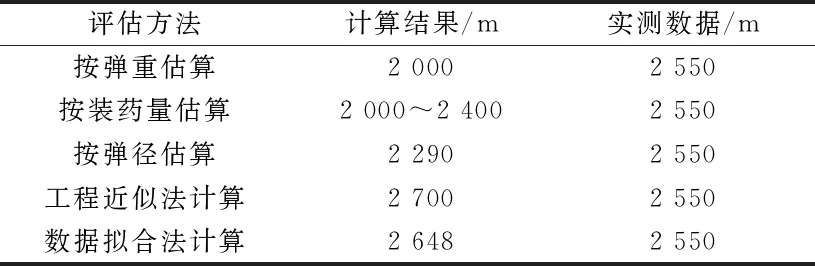
表5 破片飞散距离评估方法比较

4 结论

1)安全距离的评估方法主要有估算法、工程近似法与数据拟合法。进行安全距离评估时，首先采用估算法(分别按照弹的质量、弹径、装药量估算)进行大致估算，然后再按照工程近似法与数据拟合法进行综合评估。数据拟合法精度最好，工程近似法次之，估算法最差。

2)综合比较工程近似法与数据拟合法可知,工程近似法R涉及到海拔高度h(y)、破片迎风阻力系数CD、破片质量Me、破片K值等参数值，变量较多，取值复杂。数据拟合法R与μ关系密切，且随破片体积的增大而增大，μ=3时为最大安全距离，方法简单，安全可靠。

3)基于各种估算与计算结果，无论粗短型弹药还是细长型弹药，本次实弹打靶破片飞散安全距离最大不超过2 .7 km, 小于实弹打靶弹着点与观测台最小距离3.5 km，观测台安全。