基于改进TLBO的DV-Hop定位算法

2020-03-23陈慧琴王振飞

兵器装备工程学报 2020年2期

陈慧琴，王振飞

(1.山西机电职业技术学院，山西长治 046000；2.太原理工大学机械工程学院，太原 030024)

无线传感器网络(Wireless Sensor Network,WSN)是一个由多个传感节点通过多跳方式组成的自组织网络，它对环境的适应性很强，现在已被广泛应用于医疗保健、空间探索、工业控制等多种场景中[1]。大多数情况下，我们需要根据收集到的数据来确定传感器节点的确切位置，以便进行目标检测和跟踪，制定应对策略，节点定位已成为WSN中的研究热点[2]。

节点定位算法通常分为基于测距和非测距两种。基于测距的算法是在距离或角度等测量值的基础上利用定位算法估算未知节点的位置坐标[3]。该类算法有着较高的定位精度，但需要额外的硬件来测量节点间的距离，且距离的测量容易受到多径衰落的影响[4]。基于非测距的算法根据WSN中节点之间的连接信息估计未知节点的坐标。DV-Hop算法[5]是一种广泛使用的非测距定位算法，科研人员对其做了大量研究，提出许多改进的DV-Hop算法。文献[6]提出一种基于移动节点的DV-Hop优化算法，将移动节点添加到算法中，并利用双半径广播节点的位置坐标以优化节点间的跳数，提高定位精度。文献[7]提出了基于遗传算法(Genetic algorithm,GA)的DV-Hop算法，利用GA算法的交叉、选择、变异来优化定位结果。文献[8]提出一种基于最优辅助距离估计锚节点的DV-Hop定位算法，根据不同的估距类型计算节点间的估计距离，并将加权因子的概念引入到三边定位法中，以提高定位精度。文献[9]提出一种基于粒子群优化算法(Particle swarm optimization,PSO)的改进DV-Hop算法，利用二维双曲线定位算法估计未知节点的位置[10]后，再使用PSO算法提高定位准确性。本文提出一种基于改进教与学优化算法(Teaching-Learning-Based Optimization,TLBO)的DV-Hop定位算法来提高定位精度。

1 DV-Hop算法

DV-Hop算法定位步骤如下[11]。

每个锚节点Ai以多跳的方式向网络中广播包含Ai的位置以及从0开始的跳数字段的报文信息。在这个过程中，每经过一跳，跳数都会增加1。网络中的节点J(锚节点或未知节点)记录Ai的位置并初始化它和Ai之间的最小跳数，记为hopi,J。当节点J接收到的跳数值低于先前存储的跳数hopi,J时，则J将根据该较小跳数计数值更新hopi,J；否则忽略该跳数值。

用HopSizei表示锚节点的平均每跳距离为：

(1)

式(1)中：(xi,yi)和(xj,yj)分别表示锚节点i和j的坐标；hopij表示锚节点i和j之间的最小跳数。锚节点在网络中广播它的平均每跳距离，未知节点接收并保存距离最近锚节点的平均每跳距离并将其转发。

接收到平均每跳距离后，未知节点t通过式(2)计算它和锚节点i之间的距离dit，然后使用最小二乘估计就能得到未知节点的坐标。

dit=HopSizei×hopit

(2)

式(2)中：dit和hopit分别表示锚节点i和未知节点t之间的距离和最小跳数。

DV-Hop算法误差分析如下：1)在DV-Hop算法中，节点间的距离表示为平均跳距与最小跳数的乘积。由于网络拓扑的影响，节点间的实际每跳距离误差较大，当计算出的节点间平均跳距没有达到理想值，且节点在拓扑中进行连续多跳时，节点间的实际距离和计算距离就会产生较大偏差，从而导致定位结果不精确。2)由于网络拓扑的不同，节点在网络中的分布是无规律的。当未知节点周围的锚节点大于等于三个时，未知节点的定位坐标可以很快的计算得到。但是，如果参与定位的锚节点在一条直线上，未知节点的坐标就有可能无法确定，出现定位盲区，使得算法的定位精度有所降低。3)在DV-Hop算法中，通常利用最小二乘估计计算得到未知节点的坐标。但利用最小二乘估计计算未知节点的坐标会导致误差积累，严重影响定位结果的精确度。

2 改进的教与学优化算法

2.1 教与学优化算法

教与学优化算法(TLBO)[12-13]通过模拟班级中教师和学员间的教学过程寻找最优解。该算法分为两个阶段，分别是“教”阶段和“学”阶段。在“教”阶段中，学员跟随教师学习，在“学”阶段中，学员之间互相学习。

在“教”阶段中，学员跟随教师学习，获得知识，教师希望将学员的平均成绩meanstudent提高到他的水平Xteacher。学员的平均成绩和期望的平均成绩之间的差值表示为：

Difference_Mean=rand(Xteacher-TF×meanstudent)

(3)

且：

TF=round(1+rand)

(4)

式(4)中:rand表示[0,1]之间的随机数；round(x)表示对x进行四舍五入；TF表示改变平均值程度的教学因子，它的值可以设为1或2。每个学员根据式(5)进行学习，即：

Xnew,i=Xold,i+Difference_Mean

(5)

式(5)中:Xnew,i表示第i个学员学习后的状态值；Xold,i表示原来的状态值。如果Xnew,i比Xold,i优秀，那么用Xnew,i代替Xold,i。

在“学”阶段中，学员从班级里选择另外一个学员进行学习。假设Xi和Xj为两个不同的学员，则他们之间的学习过程为：

(6)

式(6)中：ri表示[0,1]之间的随机数；f(X)表示学员的适应度值。

2.2 TLBO的改进

TLBO根据贪婪算法选择最优个体，容易出现收敛速度慢、种群多样性丢失等问题。本文对传统的TLBO进行改进以增强其寻优能力和可靠性。

TLBO中的教学因子TF影响算法的寻优能力。在寻优的初期阶段，所有学员均向教师靠拢以便快速收敛至最优值。TF越大，算法的收敛速度越快，但其局部检测能力越弱。由于TF的值只能设为1或2，如果学员的适应度值比平均水平低，则种群趋向于靠近最优个体，此时若TF的值取2，算法的收敛速度就会加快；如果学员的适应度值比平均水平高，TF无论取1还是2，种群都会远离最优个体，算法的收敛速度也会降低。因此，本文对TF进行优化使其能够在每次迭代中自适应改变自身的值，以增强收敛速度和局部检测能力。TF表示为：

(7)

式(7)中：itermax表示最大迭代次数；iter表示当前迭代次数。

在TLBO中，学员通过教师的教学和学员间的交流学习两种方式提高自身成绩。在实际应用中，学员还可以通过自学习的方式主动向教师询问问题以提高成绩。基于自学习的学习过程为：

(8)

式(8)中：Xnew,i表示第i个学员学习后的状态值；Xold,i表示原来的状态值；r1、r2、r3、r4表示[0,1]之间的随机数。

Levy飞行是一种Markov随机游走过程，可以用来描述行人的行走分步轨迹、动物的觅食轨迹等随机运动[14]。在Levy飞行中，步长满足式(9)所示的重尾Levy分步，即：

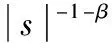
(9)

式(9)中，s表示Levy飞行的步长。

(10)

(11)

在Levy飞行中，限定范围内的局部搜索和长距离下的随机行走是相间的，因此在寻优时，部分解可以在当前最优解附近搜索，使得局部搜索能力加强；其余解则在距离当前最优解较远的范围内搜索，以确保跳出局部最优，加强全局搜索能力。将Levy飞行融入到TLBO算法中，能够在种群中产生方向剧烈变化的随机游走，扩大搜索范围，使得种群多样性增加，避免TLBO算法陷入局部最优。在基于Levy飞行的TLBO算法中，学习过程为：

(12)

式(12)中：s表示Levy飞行的步长；r1、r2、r3、r4表示[0,1]之间的随机数。

3 基于改进TLBO的DV-Hop定位算法

在基于改进TLBO的DV-Hop定位算法中，针对锚节点平均每跳距离的不准确问题，利用修正因子来修正锚节点的平均每跳距离，引入共线性概念，选择合适的锚节点进行定位以减少误差，最后，利用改进TLBO计算定位结果。

3.1 利用修正因子优化锚节点的平均每跳距离

在DV-Hop算法中，节点间距离估计的不准确性主要取决于锚节点的平均每跳距离。因此我们引入修正因子，以修正锚节点的平均每跳距离。

在DV-Hop算法的本文1.1.1节中，锚节点间的实际距离表示为：

(13)

式(13)中：(xi,yi)和(xj,yj)分别是锚节点i、j的坐标；是两个锚节点i、j之间的实际距离。

两个锚节点之间的距离还可以表示为它们之间的跳数和任一锚节点的平均每跳距离的乘积。令Dij为锚节点i、j之间的计算距离，则有：

Dij=HopSizei×hopij,i≠j

(14)

(15)

(16)

将修正因子添加到式(1)中来修正平均每跳距离，则修正后的锚节点与未知节点之间的距离为：

(17)

3.2 基于共线性的锚节点选择

在二维平面定位中，至少需要3个锚节点才能够确定未知节点的坐标。当参与定位的锚节点共线时，未知节点的位置有可能无法确定[15]。为了解决这个问题，本文引入共线度(DCL)的概念。如果三个锚节点组成的区域面积为零，则这三点共线，该区域可表示为：

(18)

式(18)中：a表示连接三个锚节点形成的区域大小；(x1,y1)、(x2,y2)和(x3,y3)表示3个锚节点的坐标。

DCL可以表示为：

(19)

根据DCL来选择锚节点以计算未知节点坐标。如果3个锚节点共线，则它们不参与到未知节点的定位中。

3.3 基于改进TLBO的定位坐标优化

定位的实质是误差的最小化问题，本节将改进TLBO算法应用到DV-Hop算法中，以减少定位误差。假设WSN中一共有N个传感器节点，其中锚节点数量为k，未知节点数量为n=N-k。定位问题的目标函数可以表示为：

(20)

利用改进TLBO算法进行坐标计算时，为了使定位误差最小，创建一个种群可行区域，并在该区域中部署WSN节点，如图1所示。假设所有节点的通信半径均为R，Nt是坐标为(xt,yt)的未知节点，A1、A2和A3是未知节点Nt的邻居锚节点，它们的坐标分别为(x1,y1)、(x2,y2)和(x3,y3)，h1,Nt、h2,Nt和h3,Nt分别是未知节点Nt与锚节点A1，A2和A3之间的最小跳数。

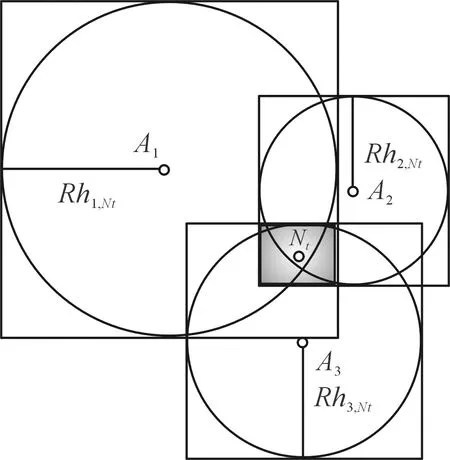
图1 种群可行区域

由于该未知节点有3个相邻锚节点，因此，分别以锚节点A1，A2和A3为圆心，R×hi,Nt(i=1,2,3)为半径构造3个圆，并给出他们的外接正方形。图中阴影区域表示3个正方形的重叠区域，即种群可行区域，未知节点Nt就处在该区域中。在该区域内随机生成种群，未知节点Nt(xt,yt)的坐标处在该可行区域内时有最小误差。随机生成的种群根据设定的上界和下界搜索未知节点的精确坐标，上界和下界可以表示为：

(21)

初始种群的最佳值设定要达到种群规模最小值和最大值间的平衡。当种群规模较小时，定位结果较差；当种群规模较大时，算法需要更多的执行时间寻找最佳方案。通过多次仿真实验可知，最优的初始种群数量为50。将随机生成的初始种群看作是学员，计算每个学员的适应度，并随机选择两个学员。这些学员是在一个未知节点的种群可行区域内随机生成的坐标，根据目标函数计算坐标值。对所有生成的坐标进行类似的处理，并根据目标函数选择具有最小误差的坐标作为未知节点的最终坐标。对于所有的未知节点，重复上述过程，直至满足停止条件。

综上所述，基于改进TLBO的DV-Hop定位算法的步骤为：

步骤1计算未知节点和锚节点之间的最小跳数以及锚节点的平均每跳距离；

步骤2利用修正因子修正每个锚节点的平均每跳距离，根据式(17)并计算未知节点和锚节点之间的距离；

步骤3根据式(18)、式(19)，利用共线度选择合适的定位锚节点；

步骤4找出每个未知节点的种群可行区域，并在可行区域中生成初始种群；

步骤5在可行区域内，根据式(21)确定每个未知节点的上界和下界的值；

步骤6寻找最优的初始种群数量，并根据目标函数计算未知节点的坐标。对于所有的未知节点，重复上述过程，直至满足停止条件。

4 仿真结果分析

4.1 参数设置

使用Matlab 2014仿真软件验证本文算法的性能，并与传统的DV-Hop算法、文献[7]提出的基于遗传算法的DV-Hop改进算法、文献[9]提出的基于粒子群优化的改进DV-Hop算法进行比较。在100 m×100 m的仿真区域内，随机生成k个锚节点和n个未知节点，所有节点的通信半径为R。在改进TLBO算法中，设置初始种群大小为50，最大迭代次数为500。为了减小算法的偶然性带来的误差，将各个算法重复运行50次，取平均值作为最终的结果。本文中，利用定位误差(Localization Error,LE)和平均定位误差(Average Localization Error,ALE)衡量算法性能。节点的实际坐标和估计坐标之间的差值LE为：

(22)

式(22)中：(xt,yt)表示未知节点的估计坐标；(xa,ya)表示未知节点的实际坐标。

ALE指总定位误差与未知节点数量的比值，可以表示为：

(23)

4.2 仿真结果分析

4.2.1定位误差比较

在100 m×100 m的仿真区域内随机部署100个节点，每个节点的通信半径为25 m，其中锚节点个数为60，未知节点个数为40。图2所示为4种算法的定位误差结果，与其他算法相比，本文算法的效果更好。在文献[7]算法中，需要设置遗传算法的最佳控制参数以获得更精确的定位结果，但遗传算法可能无法达到全局最优和局部最优之间的完美平衡。本文算法利用修正因子提高了锚节点平均每跳距离的准确性，并且根据共线性选择，处在非同一直线上的锚节点参与定位，提高了定位精度。

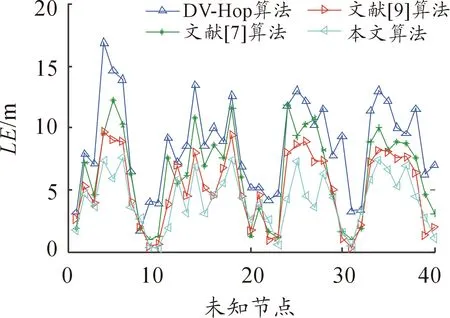
图2 利用不同算法得到的未知节点定位误差曲线

表1所示为利用4种算法获得的定位误差的最大值、最小值和平均值。从表1可以看出，本文算法在定位精度方面与其他定位算法相比性能更好，最大定位误差和最小定位误差都有明显的下降，平均定位误差为4.18m，定位精度提高很多。

表1 定位误差

4.2.2锚节点比值对定位结果的影响

锚节点比值会影响算法的定位精度。在100 m×100 m的仿真区域内随机部署100个节点，每个节点的通信半径为30 m，锚节点比值从20%增加到70%。图3为四种算法的ALE随锚节点比值变化图。在锚节点比值逐渐增大的过程中，4种算法的ALE均在减小。这是因为未知节点和锚节点之间的跳数值随着锚节点数量的增加而下降，并且锚节点的平均每跳距离和跳数值有着密切关系，即当跳数值较小时，平均每跳距离越精确，所以，当锚节点的个数越多时，其平均每跳距离的值也就越精确。因此，4种算法的ALE都随着节点密度的增加而降低。对比4种算法的ALE，本文算法的ALE是最小的，当锚节点比值为70%时，本文算法的ALE可以达到3.17 m

4.2.3通信半径对定位结果的影响

节点的通信半径同样影响算法的定位精度。在100 m×100 m的区域内随机部署100个节点，其中锚节点比值为30%，节点的通信半径从15 m增加到40 m。图4为不同通信半径情况下4种算法的ALE。仿真结果表明，随着通信半径的增大，4种算法的ALE先减小，当通信半径大于35 m时，ALE基本维持不变。然而，本文算法的ALE始终是最小的。通信半径的增加会使节点周围能够通信的节点数量变多，锚节点的平均每跳距离更加精确，并且本文算法还根据修正因子进一步修正平均每跳距离，这样锚节点和未知节点间的距离就会更精确，再根据改进TLBO算法，就能得到未知节点精确的坐标。

图3 4种算法的ALE随锚节点比值的变化

图4 4种算法的ALE随通信半径的变化

4.2.4节点密度对定位结果的影响

在WSN中，定位精度还与节点密度有关。图5为在不同节点密度时的ALE。在100 m×100 m的区域内随机部署节点，节点总数从50增加到400，节点的通信半径为25 m，且锚节点比例为30%。从图5可知，节点密度增加时，4种算法的ALE逐渐减小。因为随着节点密度的增加，网络连通性也在增加，WSN中能够收集到的用于节点定位的信息也越来越多，定位精度会提高。当WSN中的节点数量达到一定的值后，网络连通性的加强对定位结果的影响就会很小。与其他算法相比，本文算法在定位精度方面表现出更好的性能。因为网络连通性的增强使得算法可以找到多组不共线的锚节点来定位同一个未知节点，这样，该未知节点的定位精度会提高很多。图5中，当节点总数为300时，本文算法的ALE为4.72 m，DV-Hop算法、文献[7]算法、文献[9]算法的ALE分别为6.97 m、6.25 m、5.61 m，相比之下，本文算法的ALE分别提高了32.28%、24.48%、15.86%。